Содержание
- 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛИННОЙ ЛИНИИ. погонные параметры Рассмотрим двухпроводную длинную линию. ZН = RН + iXН —
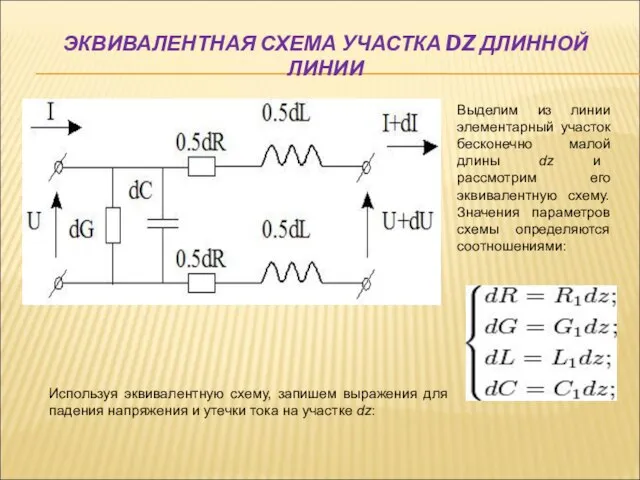
- 3. ЭКВИВАЛЕНТНАЯ СХЕМА УЧАСТКА DZ ДЛИННОЙ ЛИНИИ Выделим из линии элементарный участок бесконечно малой длины dz и
- 4. Обозначив Z1 = R1 + iωL1, - полное продольное сопротивление участка dz, а Y1 = G1
- 5. решения известны и могут быть записаны в виде: Данные соотношения являются математическим определением регулярности длинной линии.
- 6. Таким образом, коэффициенты AU, AI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а
- 7. Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен
- 8. При этом фазовая скорость волны в линии VФ определяется через коэффициент фазы: Определим коэффициенты A и
- 9. где — волновое сопротивление линии. В этом случае получим Для определения коэффициентов A и B в
- 10. Подставив полученные значения коэффициентов, после преобразований получим: Рассмотрим простейший случай, когда напряжение и ток в линии
- 11. На рисунке 2 представлена затухающая синусоида прямой волны. Перемещение волны характеризуется фазовой скоростью. Это скорость перемещения
- 12. ПЕРВИЧНЫЕ ПАРАМЕТРЫ ПЕРЕДАЧИ ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ. Электрическое сопротивление кабельной цепи это достаточно сложное понятие т.к. это сопротивление
- 13. ПЕРЕМЕННЫЙ ТОК Полное сопротивление цепи на переменном токе складывается из четырех составляющих: где R0 - сопротивление
- 14. ПОВЕРХНОСТНЫЙ ЭФФЕКТ Плотность тока на поверхности проводников на высоких частотах максимальна на поверхности и убывает по
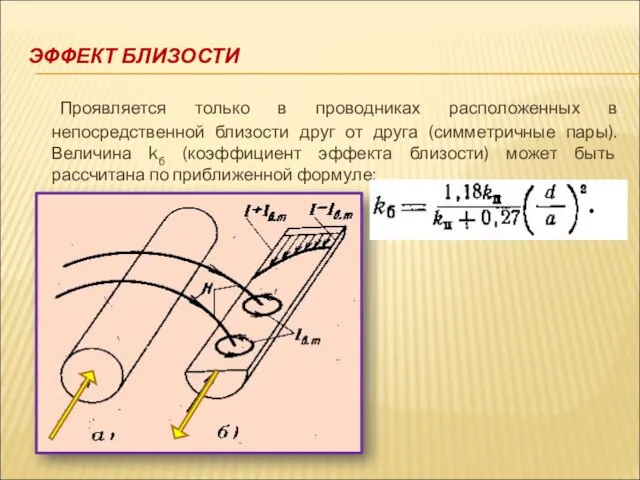
- 15. ЭФФЕКТ БЛИЗОСТИ Проявляется только в проводниках расположенных в непосредственной близости друг от друга (симметричные пары). Величина
- 16. ПОТЕРИ В ОКРУЖАЮЩИХ МЕТАЛЛИЧЕСКИХ МАССАХ Окружающие металлические массы за счет проникновения в них электромагнитного поля также
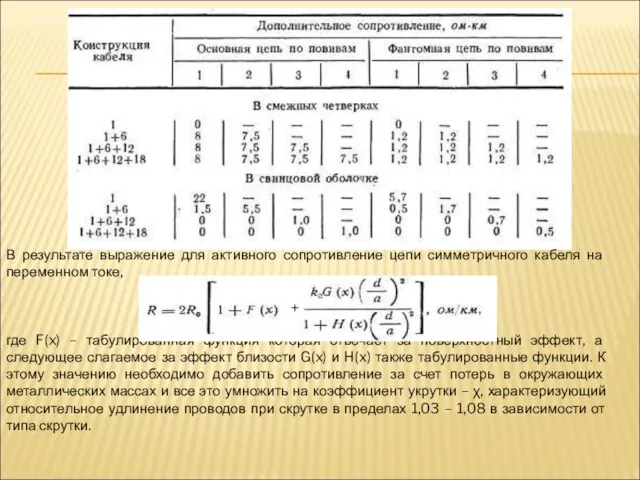
- 17. В результате выражение для активного сопротивление цепи симметричного кабеля на переменном токе, где F(x) – табулированная
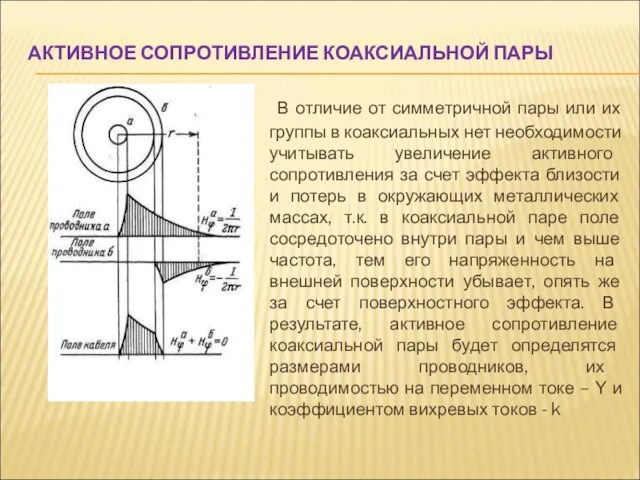
- 18. АКТИВНОЕ СОПРОТИВЛЕНИЕ КОАКСИАЛЬНОЙ ПАРЫ В отличие от симметричной пары или их группы в коаксиальных нет необходимости
- 19. В этом случае
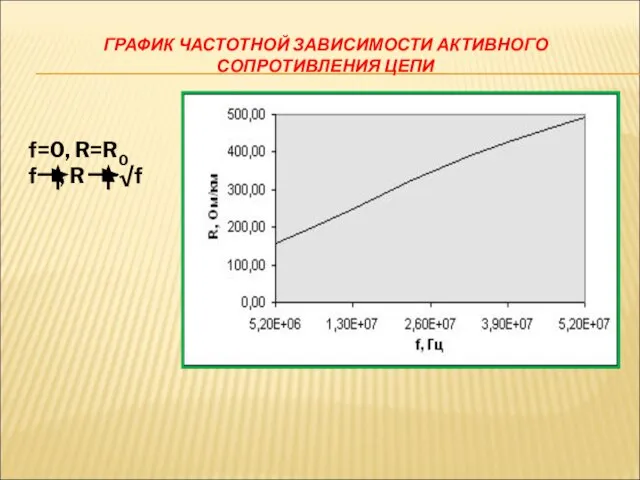
- 20. ГРАФИК ЧАСТОТНОЙ ЗАВИСИМОСТИ АКТИВНОГО СОПРОТИВЛЕНИЯ ЦЕПИ f=0, R=R0 f , R ~√f
- 21. ИНДУКТИВНОСТЬ Индуктивность цепи характеризуется отношением магнитного потока Ф к току I, создавшему этот поток: Различают внутреннюю
- 22. Внешняя индуктивность одножильного провода, а также внешняя индуктивность коаксиального кабеля Внутренняя индуктивность проводов коаксиальной пары, d
- 23. ПЕРЕДАЧА ЭНЕРГИИ ПО СИММЕТРИЧНОЙ ЦЕПИ С УЧЕТОМ ПОТЕРЬ Для определения параметров симметричной цепи с потерями необходимо
- 24. Дифференциальное уравнение второго порядка для определения компонент поля имеет вид: Для определения Еz и Hφ симметричной
- 25. - для проводников - для диэлектриков Составляющую Нφ определяем из ранее приведенного выражения:
- 26. В симметричных кабелях, в отличие от коаксиальных, нет симметрии в расположении электромагнитного поля вокруг проводника, т.е.
- 27. Соответственно составляющая магнитного поля Полученные уравнения аналогичны уравнению для внутреннего проводника коаксиального кабеля. Отличие заключается в
- 28. Решением данного уравнения является Составляющая магнитного поля где Вn , Сn — постоянные интегрирования, для нахождения
- 29. ОКОНЧАТЕЛЬНЫЕ ВЫРАЖЕНИЯ ДЛЯ R И L В СИММЕТРИЧНОМ КАБЕЛЕ При парной скрутке р = 1, при
- 30. ИНДУКТИВНОСТЬ СИММЕТРИЧНОЙ ЦЕПИ Выше было определено значение внутренней индуктивности проводников. Индуктивность цепи в целом определяется суммой
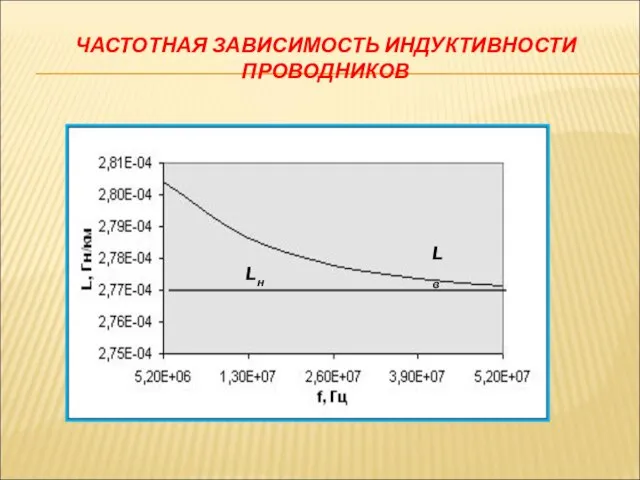
- 31. ЧАСТОТНАЯ ЗАВИСИМОСТЬ ИНДУКТИВНОСТИ ПРОВОДНИКОВ Lв Lн
- 32. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ Емкость коаксиальной пары, включая радиочастотные кабели определяется выражением: Емкость кабелей измеряют и нормируют в
- 33. СИММЕТРИЧНЫЕ ПАРЫ Емкость одной жилы двухжильного кабеля в общей металлической оболочке и одной жилы симметричного экранированного
- 34. Частичные емкости в четверке С10, С20, С30, С40 – емкости по отношению к металлической оболочке, С12,
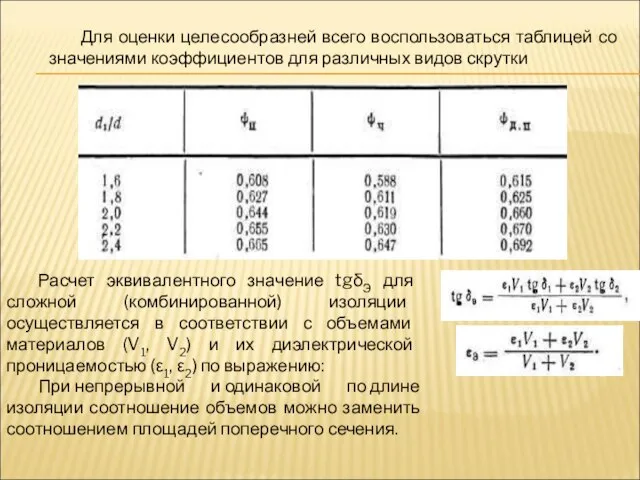
- 35. Для оценки целесообразней всего воспользоваться таблицей со значениями коэффициентов для различных видов скрутки Расчет эквивалентного значение
- 36. ПРОВОДИМОСТЬ ИЗОЛЯЦИИ Проводимость изоляции между токоведущими жилами кабеля в общем случае складывается из двух составляющих: G0
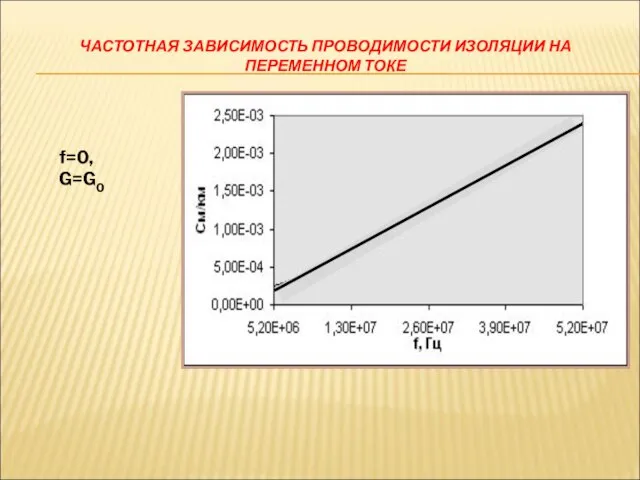
- 37. ЧАСТОТНАЯ ЗАВИСИМОСТЬ ПРОВОДИМОСТИ ИЗОЛЯЦИИ НА ПЕРЕМЕННОМ ТОКЕ f=0, G=G0
- 39. Скачать презентацию




























 Повесть Л.Н.Толстого «Хаджи-Мурат»
Повесть Л.Н.Толстого «Хаджи-Мурат» Травмы, заболев суставов
Травмы, заболев суставов Установочная конференция по практике производственной (проектно-технологической)
Установочная конференция по практике производственной (проектно-технологической) ОТКРЫТЫЙ УРОК ПО ФИЗИКЕ В 9 КЛАССЕ
ОТКРЫТЫЙ УРОК ПО ФИЗИКЕ В 9 КЛАССЕ Не пугайте малыша незнакомцами
Не пугайте малыша незнакомцами Работа с БД из Java-программ: JDBC www.spro-club.ru
Работа с БД из Java-программ: JDBC www.spro-club.ru Семинар по проблеме:«Организация внеурочной деятельности по ФГОС в начальной школе».
Семинар по проблеме:«Организация внеурочной деятельности по ФГОС в начальной школе».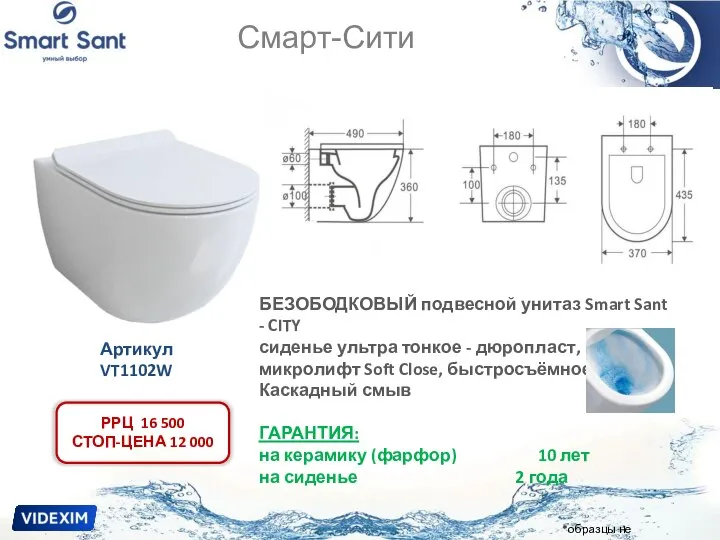 Новинки Смарт Сити подвесной унитаз
Новинки Смарт Сити подвесной унитаз Социальная компания Бірлік Life, проект Без долгов
Социальная компания Бірлік Life, проект Без долгов Металлы в строительстве
Металлы в строительстве Примерная программа духовно-нравственного развития, воспитания обучающихся на ступени начального общего образования.
Примерная программа духовно-нравственного развития, воспитания обучающихся на ступени начального общего образования. Современный учитель: профессиональная компетентность современного учителя
Современный учитель: профессиональная компетентность современного учителя Три мира в романеМ.Булгакова «Мастер и Маргарита»
Три мира в романеМ.Булгакова «Мастер и Маргарита» Европейската Схема за екомаркировка в България Инструмент за устойчиво потребление и производство. - презентация
Европейската Схема за екомаркировка в България Инструмент за устойчиво потребление и производство. - презентация Формирование природно-хозяйственных комплексов своей местности
Формирование природно-хозяйственных комплексов своей местности «Человек без вредных привычек-человек будущего?!»
«Человек без вредных привычек-человек будущего?!» Урок литературного чтения
Урок литературного чтения Резюме. Місце для фото
Резюме. Місце для фото Власовец Анна Александровна,студентка 2-го курсаБрестского государственного университета имени А.С. Пушкина
Власовец Анна Александровна,студентка 2-го курсаБрестского государственного университета имени А.С. Пушкина Cercon design – CAD для Cercon
Cercon design – CAD для Cercon Online учет всех действий, происходящих в ресторане, в рамках одной программы. Официант/бармен оплачивает заказ На производстве проис
Online учет всех действий, происходящих в ресторане, в рамках одной программы. Официант/бармен оплачивает заказ На производстве проис Математическое развитие мировой цивилизации
Математическое развитие мировой цивилизации Коммерческое предложение на выполнение работ по комплексному клинингу площадей
Коммерческое предложение на выполнение работ по комплексному клинингу площадей 20140125_sankt-peterburg_-_novyy_khozyaystvennyy_uzel_rossii
20140125_sankt-peterburg_-_novyy_khozyaystvennyy_uzel_rossii Старый Новый год
Старый Новый год РДШ - старт в будущее
РДШ - старт в будущее Презентация на тему Народный фольклор потешки, считалки, колыбельные песенки, загадки
Презентация на тему Народный фольклор потешки, считалки, колыбельные песенки, загадки Антинаркотическая комиссия администрации Ростовской области
Антинаркотическая комиссия администрации Ростовской области