Движение тела под действием силы Стокса в вязкой среде

Цели работы
нахождение подходящей среды для реализации таких типов задач
нахождение методов перехода от физического решения задачи к компьютерным моделям
создание интерактивной среды, в которой пользователь может самостоятельно выполнять опыты в зависимости от некоторых данных (которые он сам и устанавливает)

Постановка задачи
физическая постановка задачи
цель моделирования
анализ объекта
Разработка модели
физическая модель математическая модель
компьютерная модель
Компьютерный эксперимент
проведение опытов
анализ результатов
Этапы моделирования

Покоящееся тело (маленький шарик сферической формы диаметром ~ 1 cм), радиусом r, бросается от начала оси координат со скоростями Vx и Vy, и двигается при действии силы тяжести и силы трения. Коэффициент трения среды равен k. При фиксированных геометрических параметрах тела коэффициент k является однозначной характеристикой среды. Тогда сила трения по абсолютной величине:
F = k*V
Воспользуемся II законом Ньютона и составим следующие уравнения:
Физическая модель
m
x
y
..
..
=
m
0
g
-
k
y
x
.
.
Vx
Vy
.
.
=
-k/m
-k/m
0
0
Vx
Vy
+
0
g

Математическая модель
Можно сказать, вся математическая модель сводится к решению двух уравнений, являющимися линейными дифференциальными уравнениями с постоянными коэффициентами, при следующих начальных условиях
Vx
=
-
k
m
Vx
.
Vy
.
-
k
m
Vy
=
+
g
Vx = x
Vx = x
.
.
..
Vy = y
Vy = y
.
.
..
y
..
-
k
m
y
=
+
g
.
x
=
-
k
m
x
..
.
Удобнее сразу решать следующие уравнения относительно координат

Математическая модель
Мы получаем две задачи Коши:
x = - x
x(0) = Vox
x(0) = xo
k
m
..
..
.
.
и
y = - y + g
k
m
y(0) = Voy
.
y(0) = yo
Решениями полученных систем являются:
x = xo+ - l-mt/k = xo + (1 – l-mt/k)
mVox
k
mVox
k
mVox
k
y = yo – g + m + t+( - )l-kt/m
m2
k2
Voy
k
gm
k
m2g
k2
mVoy
k

Условно эту часть работы можно разбить на три:
1)Создание главных объектов (сетки, шарика и кнопок) и прорисовка основных элементов сцены
2)Создание интерфейса
3)Разработка средств вывода результатов
Компьютерная модель

прорисовка шарика, координатной сетки, кнопок управления
Создание главных объектов
снабжение их программными кодами
первоначальное тестирование системы

Интерфейс
регуляторы для ввода начальных данных
возможность управления временем
режимы проведения эксперимента
программная реализация
тестирование кода

Средства вывода
динамические поля вывода
графики
замена условных величин на фактические

Проведение опытов
выбор режима
изменение начальных данных
построение графиков

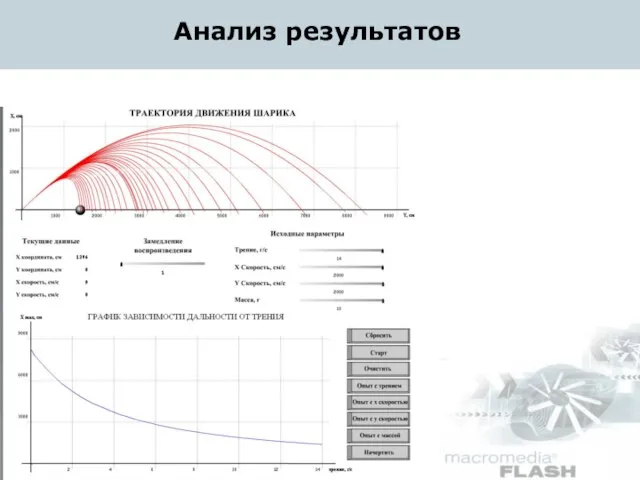
Анализ результатов