Содержание
- 2. Характеристика задания С3 Нацелено на проверку умения построить дерево игры по заданному алгоритму и обосновать выигрышную
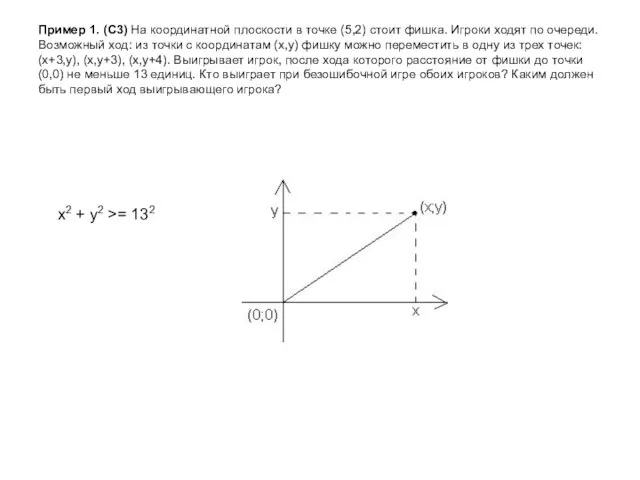
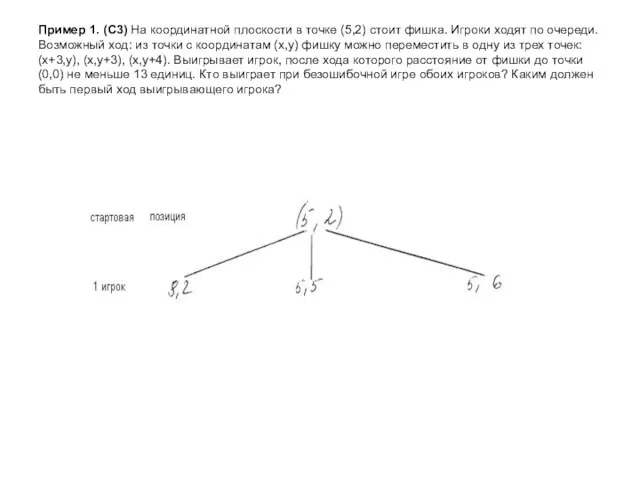
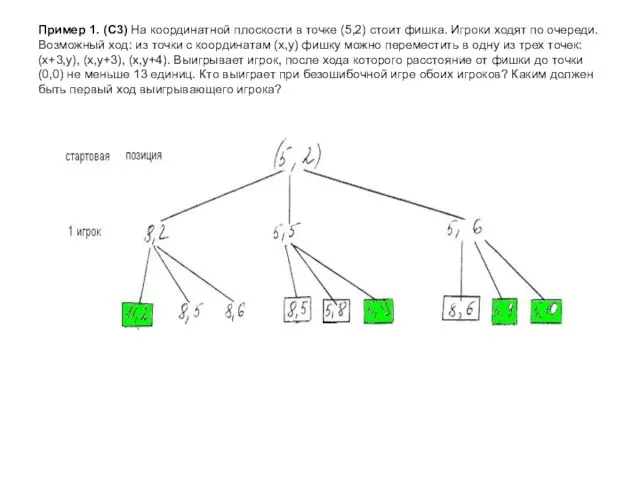
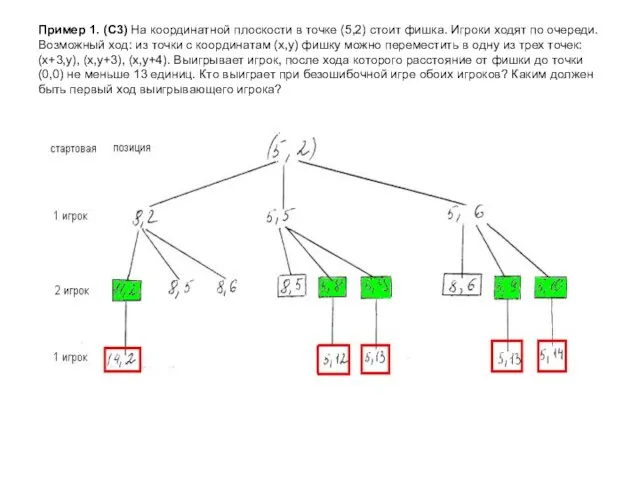
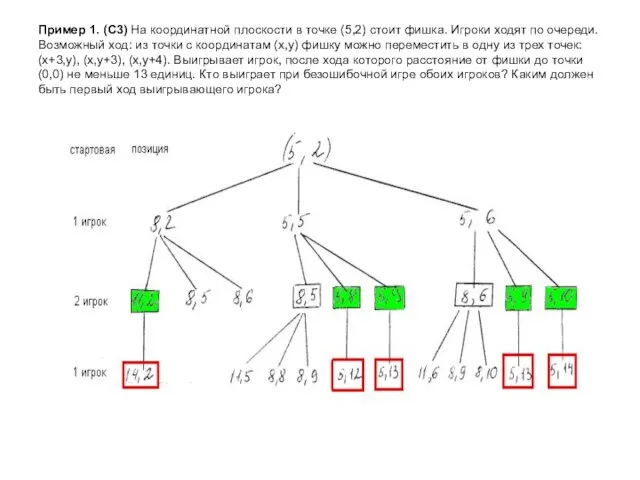
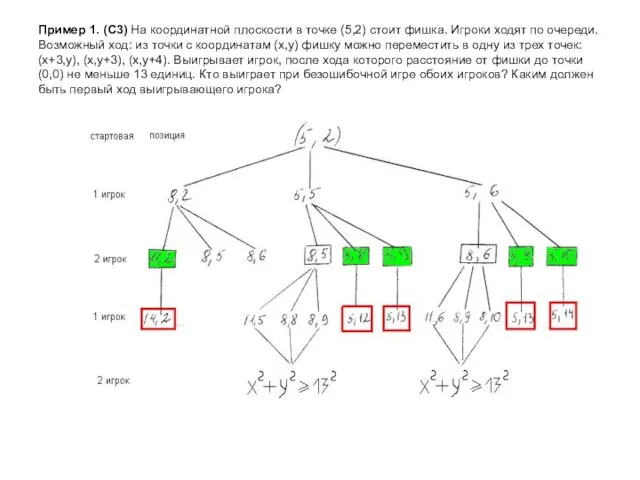
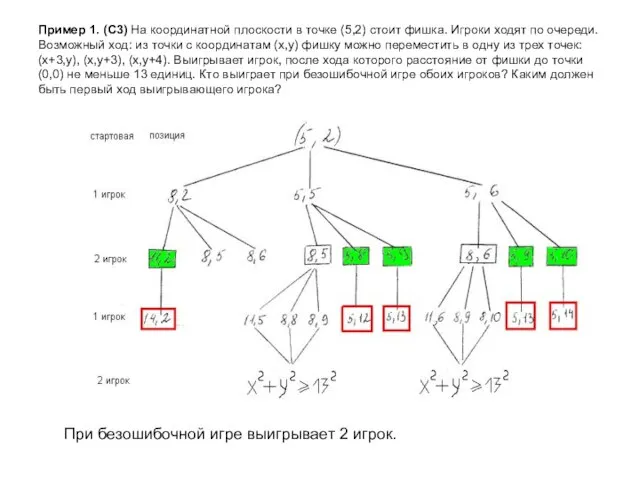
- 4. Пример 1. (С3) На координатной плоскости в точке (5,2) стоит фишка. Игроки ходят по очереди. Возможный
- 5. Пример 1. (С3) На координатной плоскости в точке (5,2) стоит фишка. Игроки ходят по очереди. Возможный
- 6. Пример 1. (С3) На координатной плоскости в точке (5,2) стоит фишка. Игроки ходят по очереди. Возможный
- 7. Пример 1. (С3) На координатной плоскости в точке (5,2) стоит фишка. Игроки ходят по очереди. Возможный
- 8. Пример 1. (С3) На координатной плоскости в точке (5,2) стоит фишка. Игроки ходят по очереди. Возможный
- 9. Пример 1. (С3) На координатной плоскости в точке (5,2) стоит фишка. Игроки ходят по очереди. Возможный
- 10. Пример 1. (С3) На координатной плоскости в точке (5,2) стоит фишка. Игроки ходят по очереди. Возможный
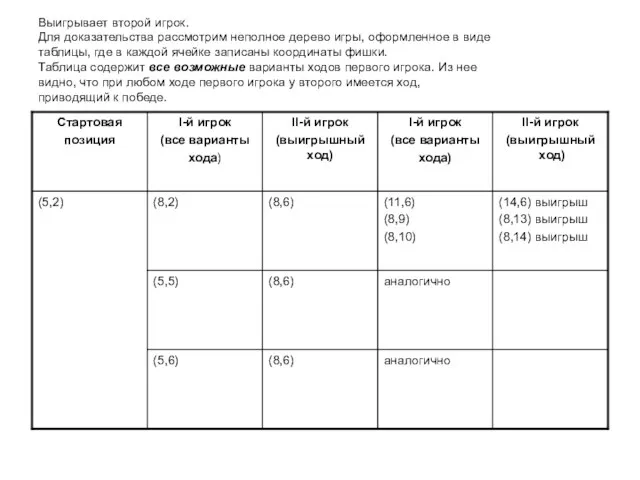
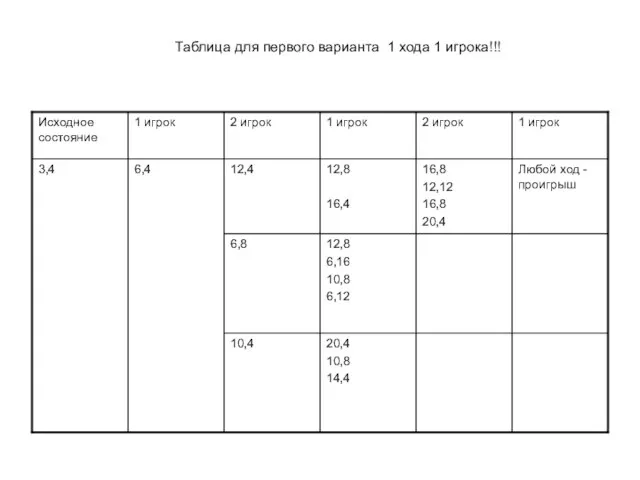
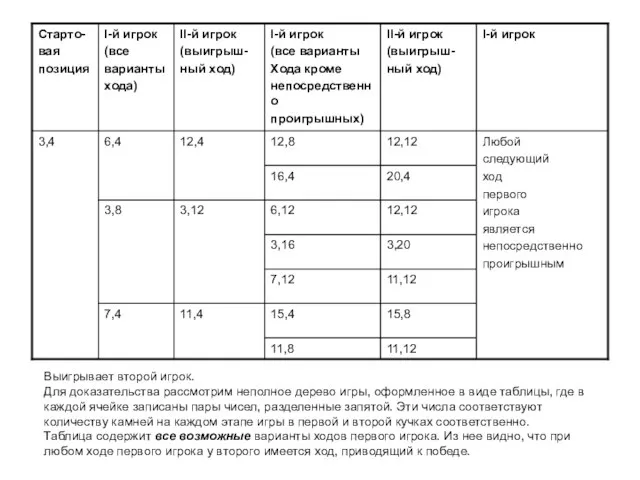
- 11. Выигрывает второй игрок. Для доказательства рассмотрим неполное дерево игры, оформленное в виде таблицы, где в каждой
- 12. Пример 2. (С3) Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в
- 13. Таблица для первого варианта 1 хода 1 игрока!!!
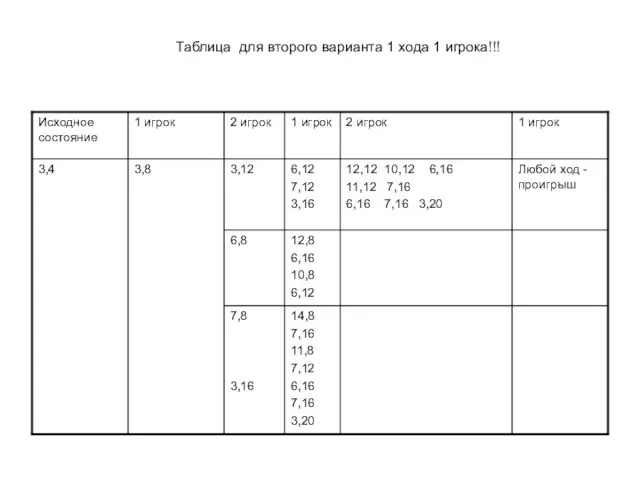
- 14. Таблица для второго варианта 1 хода 1 игрока!!!
- 15. Выигрывает второй игрок. Для доказательства рассмотрим неполное дерево игры, оформленное в виде таблицы, где в каждой
- 16. Характеристика задания С4 Нацелено на проверку умения создавать собственные программы для решения задач средней сложности. Проверяется
- 17. Типичная постановка задачи С4 содержит: Формат входных данных. Назначение программы, т.е. какую информацию программа должна извлечь
- 18. Пример задачи
- 19. Формат входных данных
- 20. Назначение программы: Формат выходных данных: Дополнительные условия и рекомендации :
- 24. Скачать презентацию










 Право Франции. Понятие и виды обязательств. Условия действительности договора
Право Франции. Понятие и виды обязательств. Условия действительности договора How to write a personal letter
How to write a personal letter Жилой комплекс комфорт-класса в центре города Чехов
Жилой комплекс комфорт-класса в центре города Чехов Abstrakcija 5.kl
Abstrakcija 5.kl Отчет группы учащихся 4 «А» класса об участии в проекте «Орфограмма в «Занковке»
Отчет группы учащихся 4 «А» класса об участии в проекте «Орфограмма в «Занковке» Природа Дальнего Востока
Природа Дальнего Востока Этапы разработки комплекса маркетинговых коммуникаций
Этапы разработки комплекса маркетинговых коммуникаций Шаблон презентации
Шаблон презентации Урок русского языка
Урок русского языка ИКТ в помощь учителю химии и биологии
ИКТ в помощь учителю химии и биологии Аргументация собственной позиции
Аргументация собственной позиции Контрактная система
Контрактная система  Субъекты политики. Правящая элита
Субъекты политики. Правящая элита Что такое темперамент. Узнай свой
Что такое темперамент. Узнай свой Слон в игре
Слон в игре Предложение Группы компаний SIS для СТАДИОНОВ
Предложение Группы компаний SIS для СТАДИОНОВ КОМПЛЕКСНЫЙ ПОДХОД К ОКАЗАНИЮ ОНКОЛОГИЧЕСКОЙ ПОМОЩИ НАСЕЛЕНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ
КОМПЛЕКСНЫЙ ПОДХОД К ОКАЗАНИЮ ОНКОЛОГИЧЕСКОЙ ПОМОЩИ НАСЕЛЕНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Бизнес проект Разведение пород крупного рогатого скота молочного направления
Бизнес проект Разведение пород крупного рогатого скота молочного направления Презентация на тему Текстовая и графическая информация
Презентация на тему Текстовая и графическая информация  Оранэль. Лесная колода
Оранэль. Лесная колода Мотивация персонала 2009
Мотивация персонала 2009 Анализ экологической политики в Казахстан е (применимо для ЦА)
Анализ экологической политики в Казахстан е (применимо для ЦА) Обзор производства стали
Обзор производства стали Комфортный микрорайон
Комфортный микрорайон Презентация12345
Презентация12345 практика
практика КАК МЫ ДУМАЕМ
КАК МЫ ДУМАЕМ Деловая игра «Выборы Президента Российской Федерации»
Деловая игра «Выборы Президента Российской Федерации»