Содержание
- 2. Электродинамические усилия (ЭДУ) в электрических аппаратах Электродинамические силы в режиме трехфазного КЗ содержат четыре составляющие: 1)
- 3. Электродинамические усилия (ЭДУ) в электрических аппаратах При КЗ развиваются значительные электродинамические силы (механические напряжения), которые могут:
- 4. Методы расчета электродинамических усилий ЭДУ определяется как результат взаимодействия проводника с током и магнитного поля (индукции)
- 5. Первый метод Направление ЭДУ, действующего на элемент с током dF = i dl х B =
- 6. Закон Био-Савара-Лапласа Индукция в точке М, создаваемая током, проходящим по всему проводнику l2
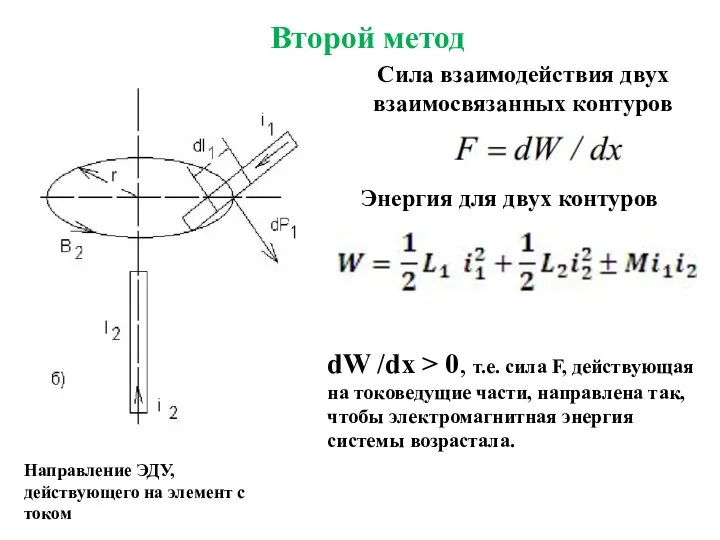
- 7. Второй метод Направление ЭДУ, действующего на элемент с током dW /dx > 0, т.е. сила F,
- 8. Электродинамические силы между параллельными проводниками бесконечной длины l – длина участка; а – расстояние между проводниками
- 9. ЭДУ между параллельными проводниками Если k = тогда
- 10. ЭДУ между параллельными проводниками Для 2-х проводников разной длины l1 ≠ l2 с любым сдвигом
- 11. Круглая и кольцевая формы сечения проводников не влияют на ЭДУ, т.к. магнитные силовые линии вокруг проводников
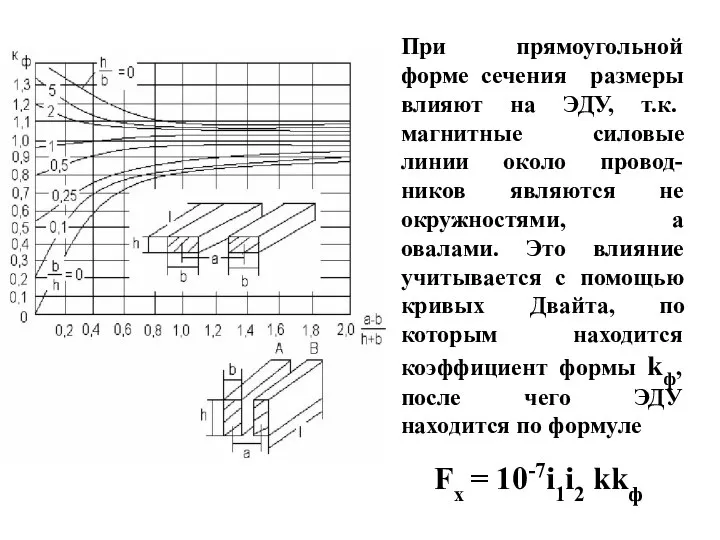
- 12. При прямоугольной форме сечения размеры влияют на ЭДУ, т.к. магнитные силовые линии около провод-ников являются не
- 13. ЭДУ, действующие на перемычку (900) При h → ∞ Сила, действующая на dx dFx = iBxdx
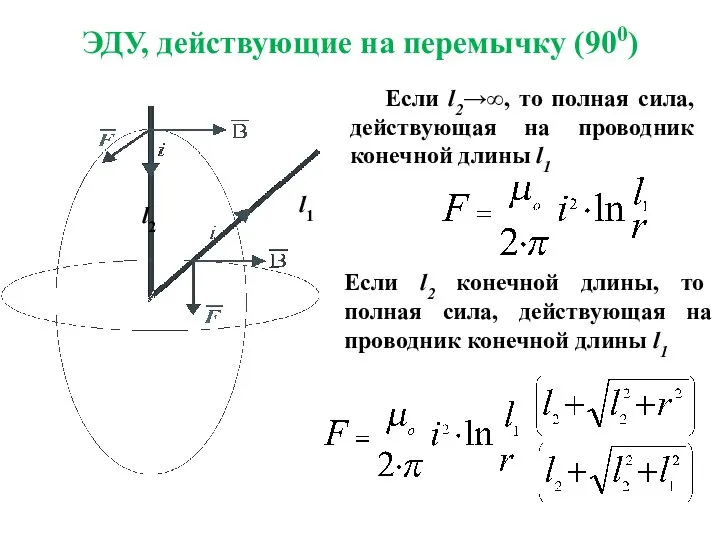
- 14. ЭДУ, действующие на перемычку (900) l1 l2 Если l2→∞, то полная сила, действующая на проводник конечной
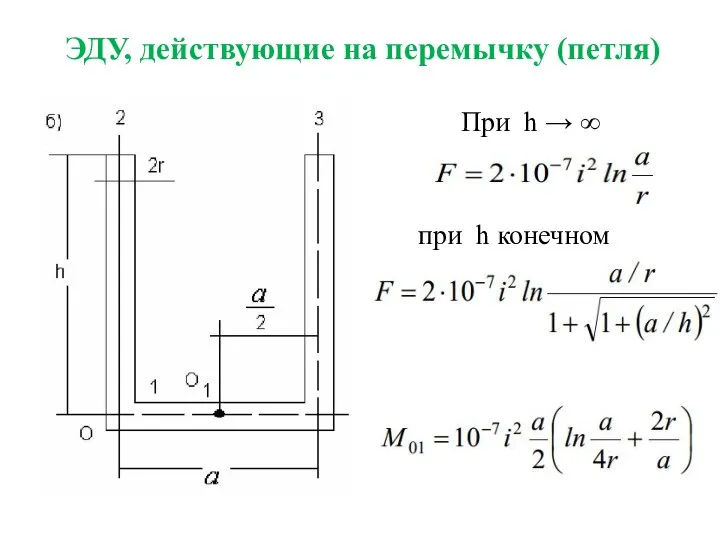
- 15. ЭДУ, действующие на перемычку (петля) При h → ∞ при h конечном
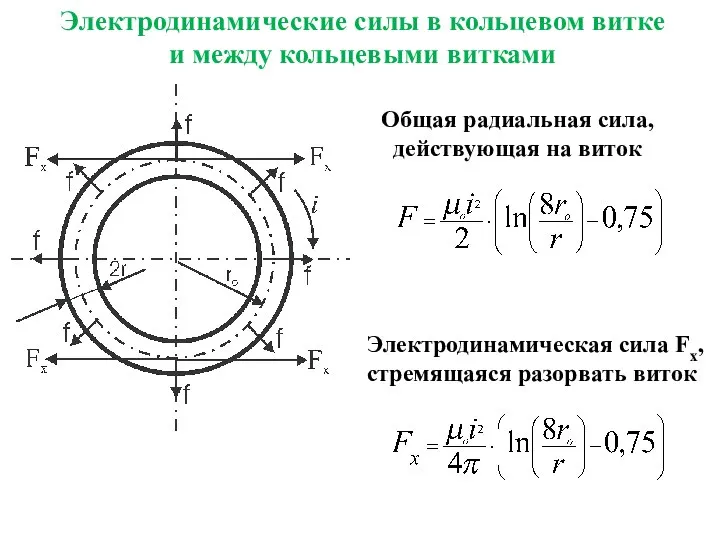
- 16. Электродинамические силы в кольцевом витке и между кольцевыми витками Общая радиальная сила, действующая на виток Электродинамическая
- 17. Для витка прямоугольного сечения Для витка круглого сечения, при R » r R
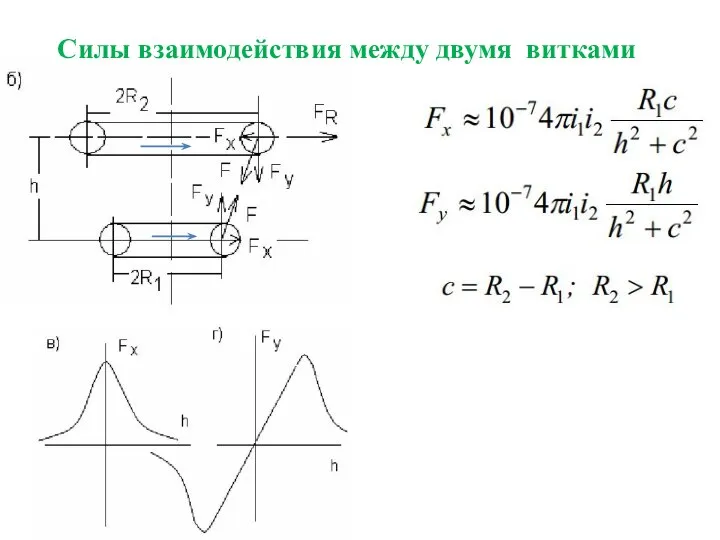
- 18. Силы взаимодействия между двумя витками
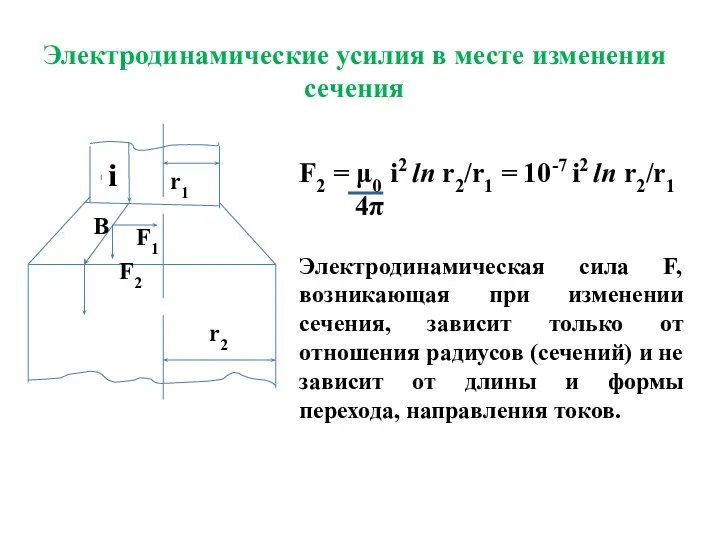
- 19. i r1 r2 F1 F2 B F2 = μ0 i2 ln r2/r1 = 10-7 i2 ln
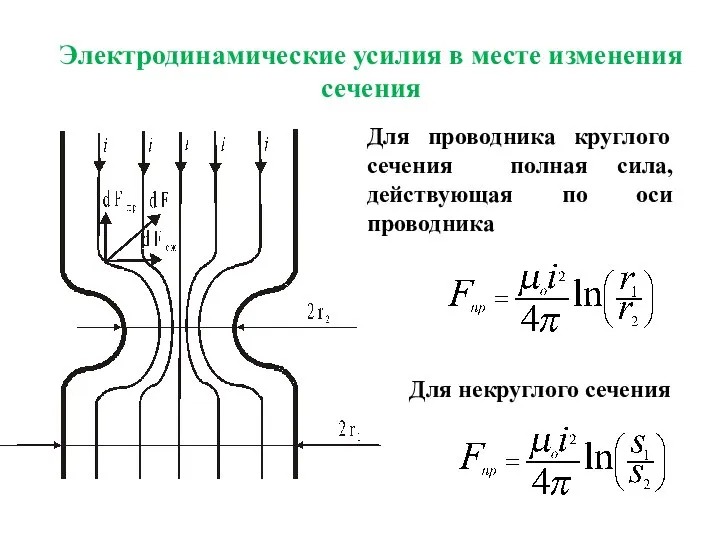
- 20. Электродинамические усилия в месте изменения сечения Для проводника круглого сечения полная сила, действующая по оси проводника
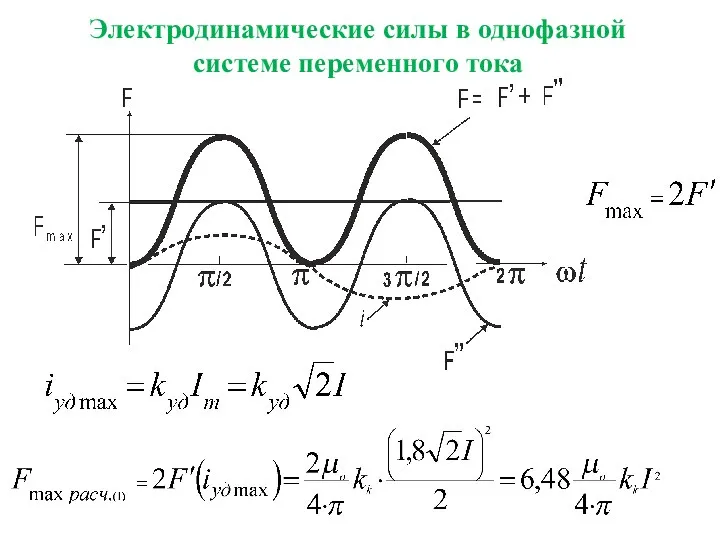
- 21. Электродинамические силы при переменном токе Однофазная система переменного тока. Ток изменяется по закону Iт – амплитудное
- 22. Электродинамические силы в однофазной системе переменного тока
- 24. Скачать презентацию












 Моделирование пенсионной системы России
Моделирование пенсионной системы России Образ Петра I в творчестве М.В. Ломоносова
Образ Петра I в творчестве М.В. Ломоносова Буквы о- а- в корнях рос раст ращ
Буквы о- а- в корнях рос раст ращ Urok_157-159_Napolnoe_soderzhanie_broylerov
Urok_157-159_Napolnoe_soderzhanie_broylerov План реализации проекта
План реализации проекта РАЗВИТИЕ ПАРТНЕРСКИХ ОТНОШЕНИЙ В ОБЛАСТИ ЖИЛИЩНОГО КРЕДИТОВАНИЯ
РАЗВИТИЕ ПАРТНЕРСКИХ ОТНОШЕНИЙ В ОБЛАСТИ ЖИЛИЩНОГО КРЕДИТОВАНИЯ Микрофлюидные МЭМС. Сенсоры для биологических и медицинских микросистем. Микронасосы. Персональный мониторинг здоровья
Микрофлюидные МЭМС. Сенсоры для биологических и медицинских микросистем. Микронасосы. Персональный мониторинг здоровья Welcome to Krasnoyarsk
Welcome to Krasnoyarsk Технология приготовления блинов и блинчиков
Технология приготовления блинов и блинчиков Елочные игрушки
Елочные игрушки Создание аксессуаров с использованием лоскутных техник
Создание аксессуаров с использованием лоскутных техник Презентация на тему Пресноводные рыбы
Презентация на тему Пресноводные рыбы Бабушка плюшевого медвежонка
Бабушка плюшевого медвежонка Памятники деревянного зодчества в Марийском крае.
Памятники деревянного зодчества в Марийском крае. Реализация профильного обучения математике в условиях сельской школы.
Реализация профильного обучения математике в условиях сельской школы. Презентация на тему Я талантлив
Презентация на тему Я талантлив Вакцины от ВПЧ. Конкурентная борьба и стратегия работы врача женской консультации.Нужна ли нам государственная программа вакцина
Вакцины от ВПЧ. Конкурентная борьба и стратегия работы врача женской консультации.Нужна ли нам государственная программа вакцина Курсы критического мышления. Школа лидерства
Курсы критического мышления. Школа лидерства Тренировка памяти
Тренировка памяти Правописание Н и НН в суффиксах имен прилагательных
Правописание Н и НН в суффиксах имен прилагательных Культура и мораль
Культура и мораль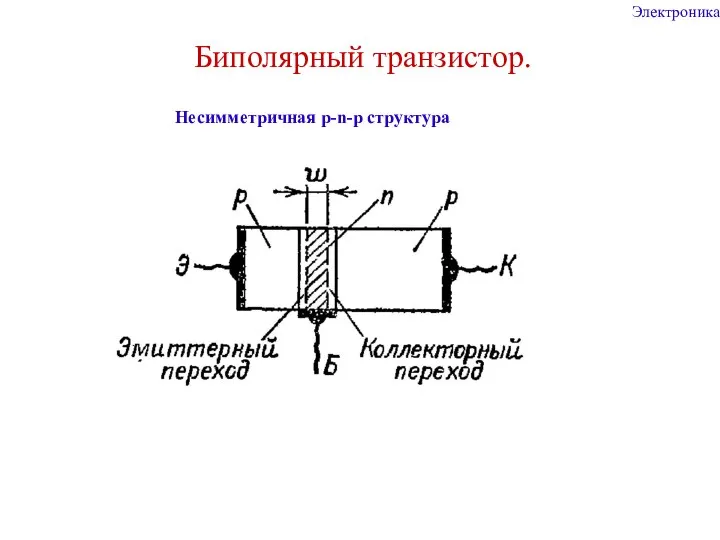 Электроника. Биполярный транзистор. Несимметричная p-n-p структура
Электроника. Биполярный транзистор. Несимметричная p-n-p структура Weihenstephan-Triesdorf University of Applied Sciences
Weihenstephan-Triesdorf University of Applied Sciences Стадии развития насекомого (3 класс)
Стадии развития насекомого (3 класс) Make up the names of animals tlephane kemony figrafe noli rohse xof tac lecrodico lowf reab regti ribtab ribd ogd.
Make up the names of animals tlephane kemony figrafe noli rohse xof tac lecrodico lowf reab regti ribtab ribd ogd. Основы организации локальных сетей Лекция 12 Тенденции развития локальных сетей Ethernet кандидат технических наук, доцент Новиков
Основы организации локальных сетей Лекция 12 Тенденции развития локальных сетей Ethernet кандидат технических наук, доцент Новиков  Пейзаж
Пейзаж РЕАЛИЗАЦИЯ ОРТОПЕДИЧЕСКИХ ИЗДЕЛИЙ В ПРЕМИАЛЬНОМ СЕГМЕНТЕ РЫНКА. - презентация
РЕАЛИЗАЦИЯ ОРТОПЕДИЧЕСКИХ ИЗДЕЛИЙ В ПРЕМИАЛЬНОМ СЕГМЕНТЕ РЫНКА. - презентация