Электромагнитное взаимодействие частиц с веществом

Физические процессы для заряженных частиц
Цель изучения – определить закономерности потерь энергии налетающих частиц в зависимости, как от характеристик самих частиц (энергия Т, скорость V, масса m, электрический заряд Z), так и от параметров среды, через которую они проходят (плотности ρ, массовое число А, заряд ядра Z, прозрачность для видимого света).
Такая детализация позволяет решать двуединую задачу:
эффективная регистрация падающего на вещество излучения;
оценка его проникающей способности с целью защиты от радиации.
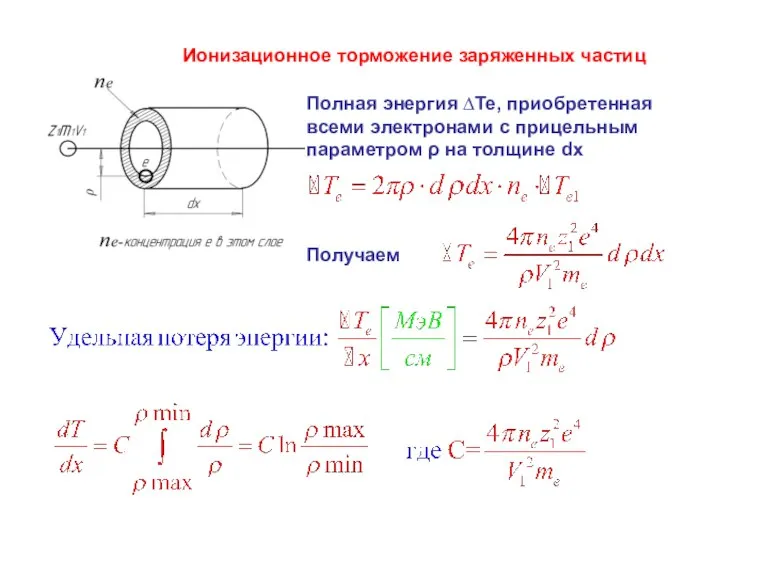
Задача решается с учетом толщины мишени (2), на которую падает частица (1): если мишень тонкая (dx), то вычисляются удельные потери энергии (dE/dx), если толстая – рассматривается процесс во всем объеме (по толщине).

Физические процессы для заряженных частиц
Упругое взаимодействие с атомными электронами (ионизационные потери заряженных частиц):
Z1 + e ? Z1 + e
2. Упругое рассеяние на ядрах (многократное рассеяние):
Z1 + Z ? Z1 + Z
3. Тормозное излучение, которое характерно только для электронов:
4. Черенковское излучение, которое возникает в прозрачной среде, если заряженная частица движется быстрее, чем скорость света (v > c/n, где n – оптический показатель преломления) .
Частица на своем пути кратковременно поляризует молекулы среды, которые при деполяризации испускают видимый свет.

Физические процессы для гамма- кванов
Упругое рассеяние на электронах среды (комптон-эффект):
Фотоэффект. Взаимодействие γ-кванта с нейтральным атомом. При этом γ-квант поглощается, выбивая из атома электрон:
Рождение электрон-позитронной пары, в электромагнитном поле ядра:
Образование каскадного ливня при попадании в вещество электрона или γ-кванта высокой энергии (больше критической). Последовательность процессов тормозного излучения и образования пар частиц в толстой мишени приводят к лавинообразному нарастанию числа вторичных частиц (е -, е+, γ) по глубине.

Ионизационное торможение заряженных частиц
Решение задачи вычисления dT/dx начнем с кулоновского взаимодействия тяжелой частицы (М1, Z1) со свободным электроном ( Т1 >> I). Частица М1 пролетает мимо е на расстоянии ρ (прицельный параметр).
Разложим силы F1 и F2 на перпендикулярные и параллельные составляющие. Эффективно действуют только перпендикулярные составляющие сил. Упрощение: заменим переменную силу, которая действует на участке 2ρ, на силу в точке перпендикулярной
Время действия силы на участке равно

Полная энергия ∆Te, приобретенная всеми электронами с прицельным параметром ρ на толщине dx
Ионизационное торможение заряженных частиц
Получаем

Учет диапазона прицельных параметров
Пусть
e
Z1
Атом вещества мишени

Ионизационное торможение заряженных частиц
Получаем формулу Бете-Блоха

График удельных ионизационных потерь энергии
dЕ/dx представляет собой потери энергии в тонком слое при фиксированной энергии Т1.
Минимум функции достигается при
или
1) - электрон связан. Энергия тратится на возбуждение атома.
2) . Здесь . Это обусловлено уменьшением эффективного времени столкновения с электронами .
3) – скорость V1 ≈ с, время столкновения мало меняется. Это приводит к минимуму dЕ/dx.
4) - начинают заметно действовать релятивистские эффекты. Вытягивание поперечного электрического поля налетающей частицы .
5) – начинается процесс экранирования поля частицы.

Ионизационное торможение заряженных частиц
На одном рисунке приведены качественные графики dЕ/dx для трех разных частиц: π±-мезона, р+- протона и α++- частицы. Кривые подобны, но смещены относительно друга, в зависимости от массы частиц и их зарядов.
С учетом эффекта
плотности
где δ – учитывает эффект плотности и имеет вид (при β → 1):
δ(β) = - ln(1 – β2) – 2ln(I/hνр) – 1, где νз – плазменная частота электронов.
Функция δ(β) компенсирует логарифмический рост dЕ/dx при высокой энергии. Практически, полное выполаживание функции dЕ/dx происходит при T1 ≈ 50 m1c2. Функция U(ß1) учитывает потери энергии на возбуждение атома.

Ионизационные потери энергии электронов
Механизм потерь энергии налетающего электрона при столкновении с электронами среды в целом аналогичен процессу взаимодействия тяжелых частиц. Особенности обусловлены малой массой налетающего электрона и обменными эффектами между тождественными частицами
Анализ этой формулы показывает, что в нерелятивистском пределе (β1<<1) при одинаковой скорости , удельные ионизационные потери протона и электрона отличаются незначительно.
Если их энергии будут одинаковы, то отношение удельных потерь в этой области будет сильно отличаться в отношении масс mр/mе.
В ультрарелятивистской области (T≈10 ГэВ) фактор зависимости от скорости (V1≈ c) пропадает, и ионизационные потери энергии выравниваются: (dЕ/dx)е/(dЕ/dx)р ≈ 2.