Содержание
- 2. Теория:
- 3. Область определения Областью определения D(y) функции y = f(x) называется множество значений аргумента х, для которого
- 4. Множество значений функции Множеством (областью) значений E(y) функции y = f(x) называется множество таких чисел y
- 5. Чётность и нечётность функции. Функция y = f(x) называется чётной, если её область определения D(f) симметрична
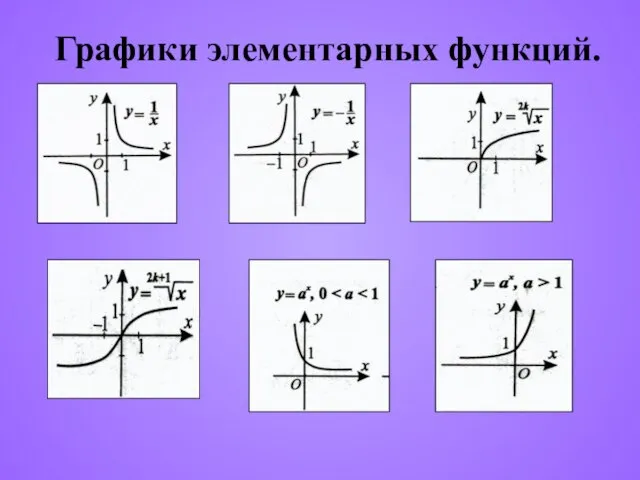
- 6. Графики элементарных функций.
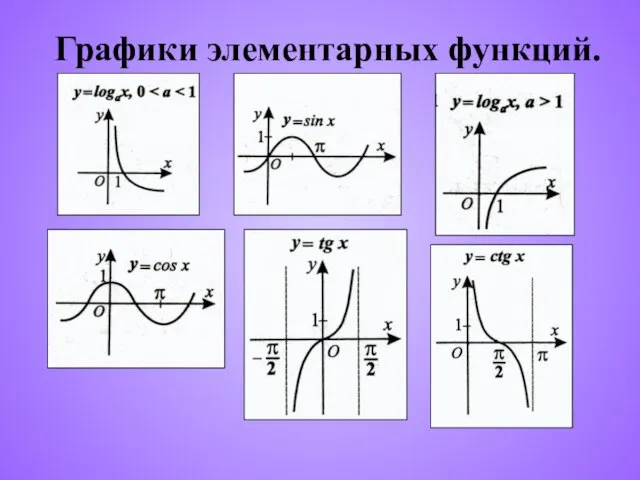
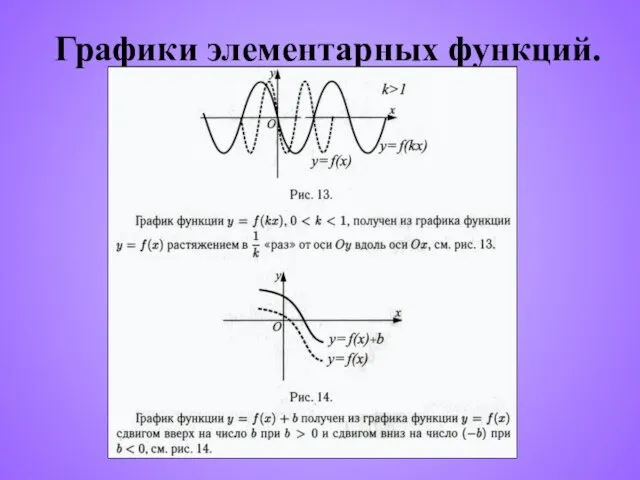
- 7. Графики элементарных функций.
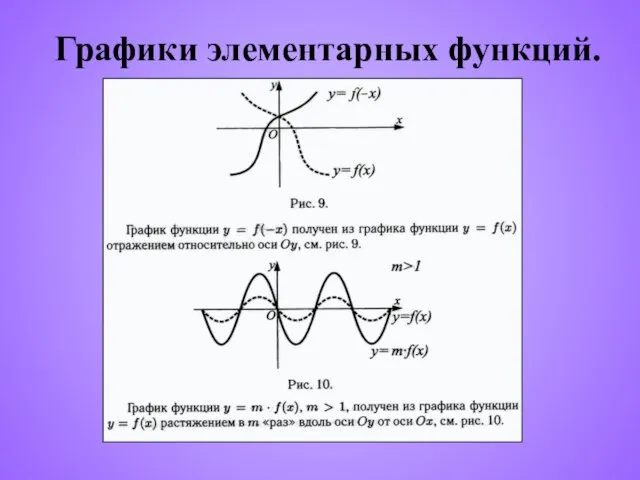
- 8. Графики элементарных функций.
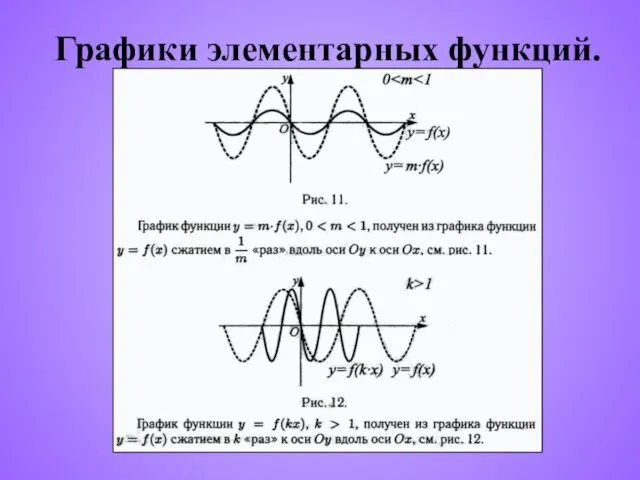
- 9. Графики элементарных функций.
- 10. Графики элементарных функций.
- 11. Таблица производных основных элементарных функций.
- 12. Геометрический смысл производной. f ’(x ) является угловым коэффициентом касательной к графику функции y = f(x)
- 13. Первообразная для основных элементарных функций.
- 14. неравенств Графическое решение
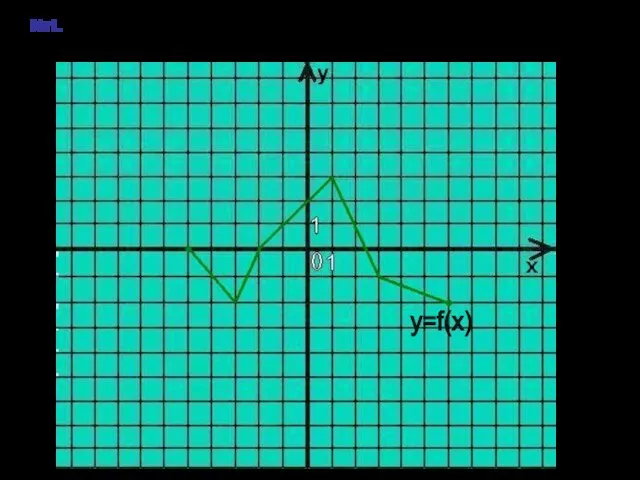
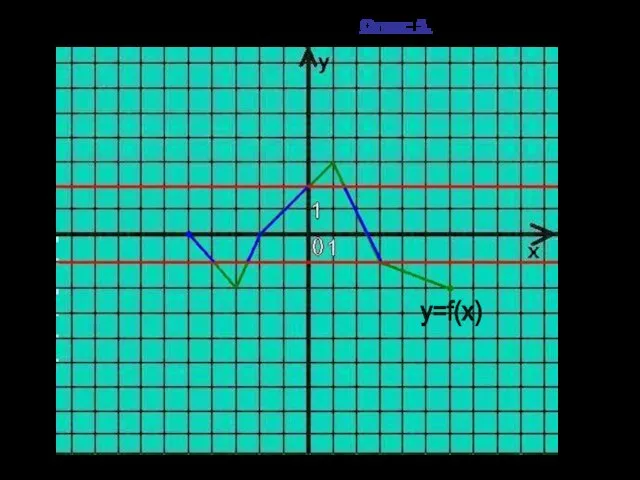
- 15. №1. На рисунке изображён график функции y=f(x). Укажите общую протяжённость отрезков, на которых выполнено условие -1
- 16. Решение:I-5-(-4)I + I-2,5-0I + I1,5-3I = 5. Ответ: 5. y=f(x)
- 17. №2. На рисунке изображён график функции y=f(x), заданной на проме- жутке [-5;5]. Укажите те значения Х,
- 18. Решение: Х с [-2;0) u (0;1] u [4;5]. - y=f(x)
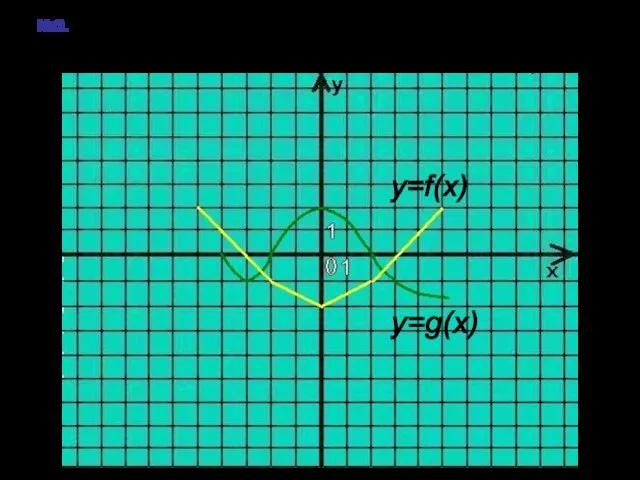
- 19. №3. На рисунке изображён график функции y=f(x) (ломаная линия) и y=g(x) (плавная линия), заданных на промежутке
- 20. Решение: f(x)>1+g(x); x c [-5;-4] u [3;5]. y=f(x) y=g(x) - y=g(x)+1
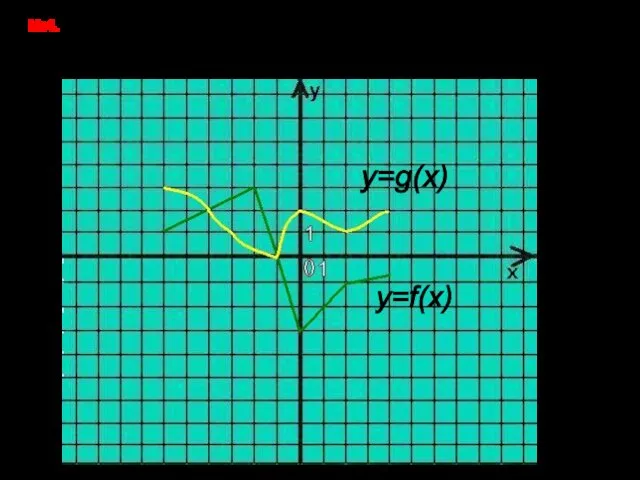
- 21. №4. На рисунке изображён график функции y=f(x) (ломаная линия) и y=g(x) (плавная линия), заданных на промежутке
- 22. Решение: Х с [-6;-4] u [2;3]. - y=g(x) y=If(x)I
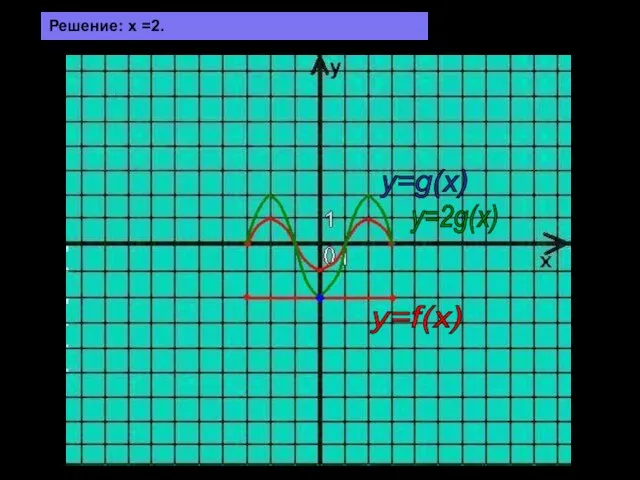
- 23. №5. На рисунке изображён график y=f(x) и y=g(x), заданные на промежутке [-3;3]. Укажите те значения х,
- 24. y=g(x) y=2g(x) y=f(x) Решение: х =2.
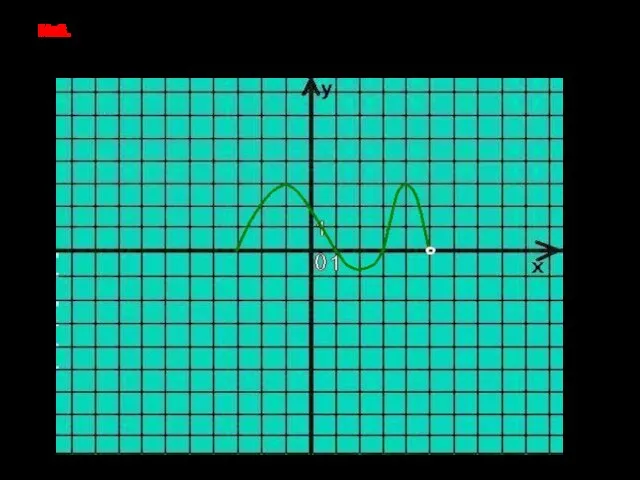
- 25. №6. На рисунке изображён график функции y=f(x). Укажите множество решений неравенства : f(x)
- 27. Скачать презентацию







![№2. На рисунке изображён график функции y=f(x), заданной на проме- жутке [-5;5].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/462949/slide-16.jpg)
![Решение: Х с [-2;0) u (0;1] u [4;5]. - y=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/462949/slide-17.jpg)
![Решение: f(x)>1+g(x); x c [-5;-4] u [3;5]. y=f(x) y=g(x) - y=g(x)+1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/462949/slide-19.jpg)
![Решение: Х с [-6;-4] u [2;3]. - y=g(x) y=If(x)I](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/462949/slide-21.jpg)
![№5. На рисунке изображён график y=f(x) и y=g(x), заданные на промежутке [-3;3].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/462949/slide-22.jpg)
 Infectious disease
Infectious disease Кто все эти люди?
Кто все эти люди? Атмосферное давление
Атмосферное давление Гигиенические требования к организации обучения детей 6-летнего возраста
Гигиенические требования к организации обучения детей 6-летнего возраста Реализация Бизнес-стратегии компании через системы управления деятельностью
Реализация Бизнес-стратегии компании через системы управления деятельностью Дорожная карта «Детство 2030»
Дорожная карта «Детство 2030» Презентация на тему Кукла из ниток
Презентация на тему Кукла из ниток Правило буравчика, левой и правой руки
Правило буравчика, левой и правой руки Vegetable Soup
Vegetable Soup All Eyes and Ears
All Eyes and Ears Радиостанции ТАКТ
Радиостанции ТАКТ Специальные налоговые режимы
Специальные налоговые режимы Число «Пи» вокруг нас
Число «Пи» вокруг нас Поэт Есенин
Поэт Есенин Атомная трагедия XX века
Атомная трагедия XX века Теоретические методы исследования
Теоретические методы исследования Формирование основных образовательных программ на основе ФГОС СПО и НПО нового поколения
Формирование основных образовательных программ на основе ФГОС СПО и НПО нового поколения Переход к предоставлению услуги «Предоставление информации об очередности предоставления жилых помещений на условиях социально
Переход к предоставлению услуги «Предоставление информации об очередности предоставления жилых помещений на условиях социально Кафедра географии, экологии и природопользования
Кафедра географии, экологии и природопользования Недвижимость как объект управления и оценки
Недвижимость как объект управления и оценки Информатика и информация
Информатика и информация «Стили детско-родительских отношений и формы личностной дезадаптации подростка».
«Стили детско-родительских отношений и формы личностной дезадаптации подростка». ИГРА
ИГРА Это надо знать
Это надо знать Презентация
Презентация Природные явления. Наводнения
Природные явления. Наводнения Становление герба Самарской губернии
Становление герба Самарской губернии Эрнест Миллер Хемингуэй
Эрнест Миллер Хемингуэй