Фильтр Винера

Учебные вопросы:
1. Постановка задачи фильтрации.
2. Интегральное уравнение
оптимального фильтра. 3. Коэффициент передачи
оптимального фильтра.
Радиотехнические цепи и сигналы. Лекция 16.

Радиотехнические цепи и сигналы. Лекция 16.
1. Постановка задачи фильтрации.
Например, пусть на вход приемника поступает смесь амплитудно-модулированного сигнала
и помехи n(t), т.е.
На вход некоторой системы (фильтра) поступает аддитивная смесь x(t) полезного сигнала s(t) и шума (помехи) n(t)
Желаемым выходом фильтра является, естественно, сигнал
Реакцией реального фильтра является оценка сигнала, т.е.
Требуется найти характеристики реального фильтра, выходное колебание которого y(t)=s*(t) отличалось бы от желаемого выхода y0(t)=s(t) с минимальной среднеквадратической погрешностью
(1)

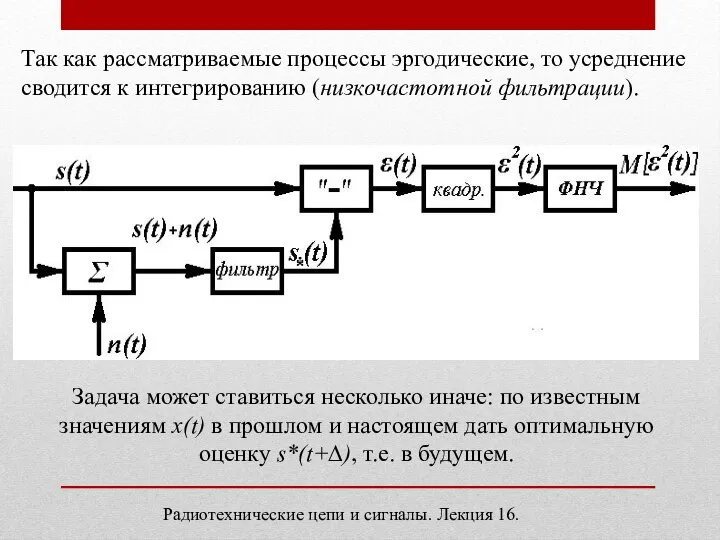
Радиотехнические цепи и сигналы. Лекция 16.
Так как рассматриваемые процессы эргодические, то усреднение сводится к интегрированию (низкочастотной фильтрации).
Задача может ставиться несколько иначе: по известным значениям x(t) в прошлом и настоящем дать оптимальную оценку s*(t+∆), т.е. в будущем.

Радиотехнические цепи и сигналы. Лекция 16.
2. Интегральное уравнение оптимального фильтра.
Более подробно рассмотрим выражение (1). При этом учтем, что выходной сигнал искомого реального фильтра определится интегралом Дюамеля
(2)
Где g(τ)- импульсная характеристика искомого реального фильтра.
Для нахождения этой характеристики определим квадрат ошибки
(3)
Усредняя левую и правую части выражения (3), получим
(4)

Радиотехнические цепи и сигналы. Лекция 16.
Учтем, что - энергия (дисперсия) сигнала s(t),
- взаимная корреляционная функция сигнала s(t) и принятого сигнала (принятой реализации) x(t),
- автокорреляционная функция принятого сигнала.
С учетом этого выражение (4) перепишется в виде
(5)
Пусть импульсная характеристика какого-то условного фильтра равна
(6)
Где h(t) - произвольная функция, не равная тождественно нулю;
Найдем среднеквадратическую ошибку фильтрации этого условного фильтра, для чего подставим в выражение (5) соотношение (6).
(7)

Радиотехнические цепи и сигналы. Лекция 16.
Очевидно, что при ошибка фильтрации минимальна, так как в этом случае g(t)=g0(t).
Перепишем формулу (7) в следующем виде
(8)
Согласно выражению (5)
(9)
Введем обозначения
(10)
(11)

Радиотехнические цепи и сигналы. Лекция 16.
Подставляя соотношения (9), (10), (11) в выражение (8), получим
(12)
Условие минимума
откуда следует
(13)
С другой стороны, как было отмечено ранее, для обеспечения минимума необходимо, чтобы . Из выражения (13) следует, что Q=0.
Преобразуем выражение (10) следующим образом, поменяв порядок интегрирования и приравняв Q=0
Так как функция h(t) - произвольная функция, не равная нулю, то, следовательно, нулю равно выражение в квадратных скобках, откуда следует:
(14)

Радиотехнические цепи и сигналы. Лекция 16.
3. Коэффициент передачи оптимального фильтра.
Применяя к обеим частям выражения (14) преобразование Фурье и используя свойства спектра свертки двух функций, получим
(15)
Где Sxs(ɷ) - взаимный энергетический спектр сигнала s(t) и принятой реализации x(t) (смеси сигнала и шума);
K0(ɷ) - коэффициент передачи мощности оптимального фильтра;
Kx(ɷ) - энергетический спектр принятой реализации x(t) (смеси сигнала и шума).
Из выражения (15) следует
(16)
Если сигнал s(t) и помеха n(t) не коррелированны между собой (что практически всегда выполняется), то