Содержание
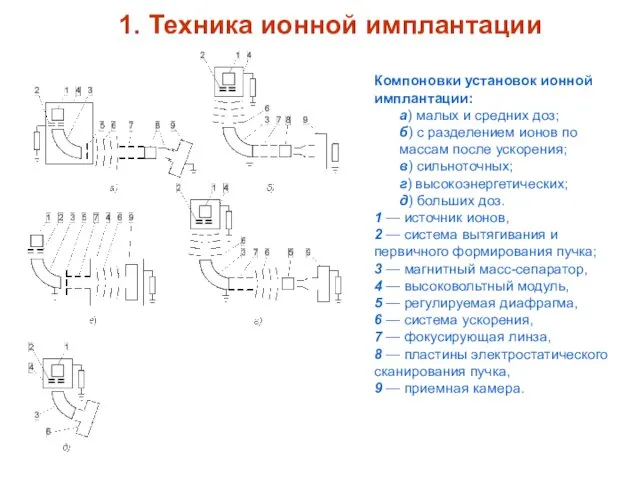
- 2. Компоновки установок ионной имплантации: а) малых и средних доз; б) с разделением ионов по массам после
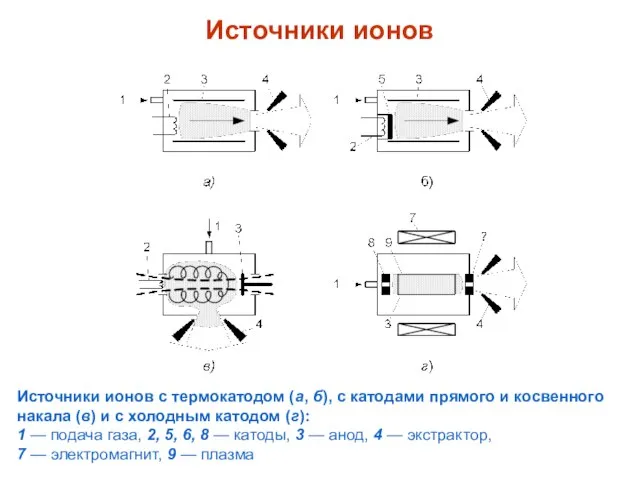
- 3. Источники ионов Источники ионов с термокатодом (а, б), с катодами прямого и косвенного накала (в) и
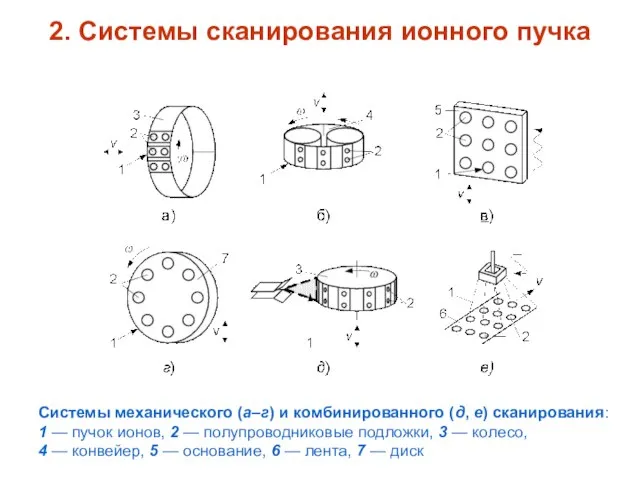
- 4. 2. Системы сканирования ионного пучка Системы механического (а–г) и комбинированного (д, е) сканирования: 1 — пучок
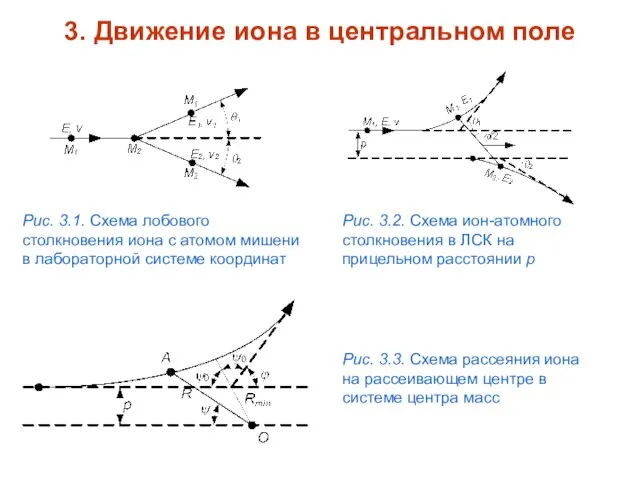
- 5. 3. Движение иона в центральном поле Рис. 3.1. Схема лобового столкновения иона с атомом мишени в
- 6. Исходя из законов сохранения энергии и момента количества движения для системы двух частиц, запишем: (3.1) (3.2)
- 7. Траектория частицы в поле неподвижного силового центра (рис. 3.3) симметрична относительно прямой, проведенной в ближайшую к
- 8. Здесь ϕ — угол отклонения частицы в силовом поле. Из (3.7) следует, что (3.9) Так как
- 9. Здесь Rmin — изображенное на рис. 3.3 минимальное расстояние, на которое частица приближается к рассеивающему центру,
- 10. Исходя из законов сохранения энергии и момента количества движения, а также геометрических соображений (рис. 3.1–3.3) можно
- 11. (3.16) Энергия атома отдачи мишени в ЛСК согласно (3.16) запишется (3.17) где параметр определяет максимально возможную
- 12. 4. Потенциалы ион-атомного взаимодействия (4.13) где Ф — функция экранирования для двухатомных систем, a — длина
- 13. Н. Бор для экранирования рассеивающего поля атомными электронами ввел эмпирический потенциал (4.16) где (4.17) (годится для
- 14. где n = 1, 2, …, Kn = const ≈ 1. При расчетах столкновений ионов с
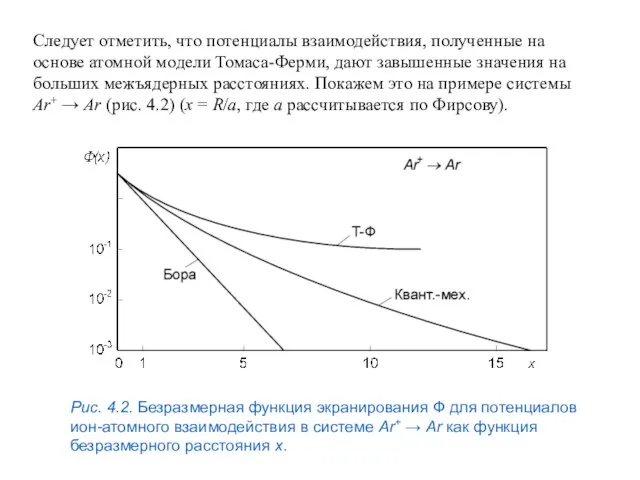
- 15. Следует отметить, что потенциалы взаимодействия, полученные на основе атомной модели Томаса-Ферми, дают завышенные значения на больших
- 16. Важной характеристикой процесса ион-атомного рассеяния является дифференциальное сечение рассеяния dσ. Если на рассеивающий центр (атом) подает
- 17. Так как имеется однозначная связь между p и ϕ,то частицы, прицельное расстояние для которых заключено между
- 18. или заменив ϕ на энергию, полученную атомом отдачи согласно (3.17) и предположив, что ϕ мало, получим
- 19. где λ′1/3 = 1,309; λ′1/2 = 0,327; λ′1 = 0,5. Потенциалы с m = 1/3 могут
- 20. Это важная формула для многих задач, в частности, при анализе материалов методом обратного резерфордовского рассеяния. Для
- 21. Поскольку ион, двигаясь в кристалле, может претерпевать столкновение с различными прицельными параметрами относительно атомов мишени p
- 22. Сечение упругого торможения (или иногда называют сечением ядерного торможения) запишется (5.1.2) (измеряется обычно в эВ·см2/атом). Учитывая
- 23. В литературе часто используется также выражение Sn(ε), которое связано с Sn(E). Учитывая (5.10) и (5.11), имеем
- 24. (5.1.7) (5.1.8) Для степенных потенциалов получим Для потенциала Томаса-Ферми
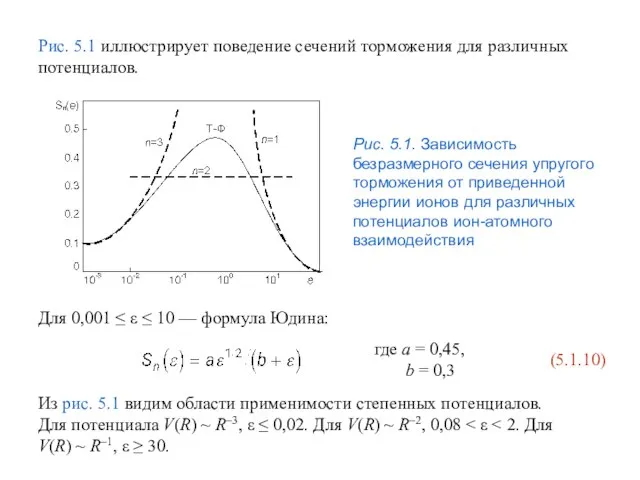
- 25. Рис. 5.1 иллюстрирует поведение сечений торможения для различных потенциалов. Рис. 5.1. Зависимость безразмерного сечения упругого торможения
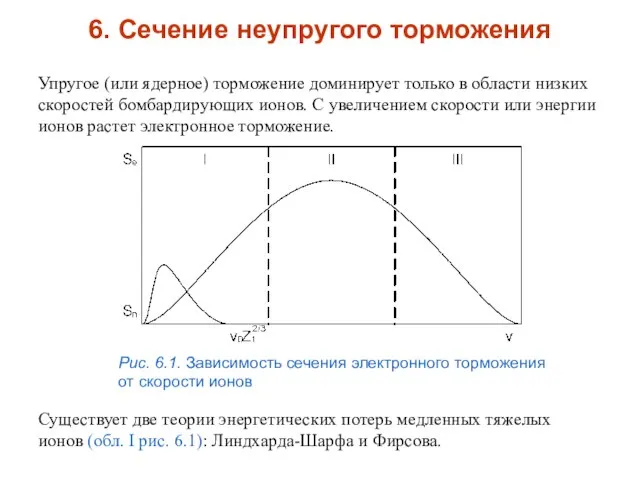
- 26. Упругое (или ядерное) торможение доминирует только в области низких скоростей бомбардирующих ионов. С увеличением скорости или
- 27. где v0 = 2,2·108 см/с — скорость электрона на первой Боровской орбите атома водорода, ξ =
- 28. Несколько иная модель электронного торможения была развита Фирсовым. В отличие от Линдхарда и Шарфа он считает,
- 29. Тогда согласно (6.3) сечение электронного торможения после интегрирования по p запишется как (6.5) или в удобном
- 30. Если скорость налетающей частицы существенно выше скорости любого атомного электрона мишени, то неупругие потери энергии описываются
- 31. При более низких скоростях тяжелый ион будет содержать определенное число связанных с ядром электронов и средний
- 32. Одной из важных характеристик, определяющих судьбу ускоренного иона, внедряемого в твердое тело, является его пробег, т.е.
- 33. Если сечение электронного и ядерного торможения известны, то суммарные потери энергии на единицу длины запишутся: (7.2)
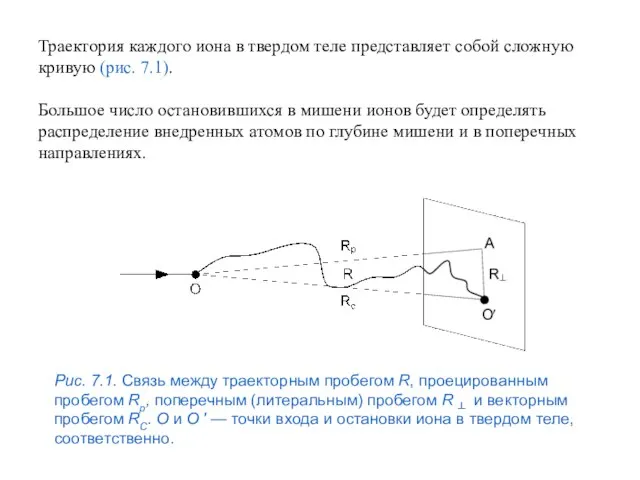
- 34. Траектория каждого иона в твердом теле представляет собой сложную кривую (рис. 7.1). Большое число остановившихся в
- 35. В настоящее время наиболее плодотворными для описания распределения внедренных атомов являются два теоретических подхода: а) метод
- 36. В рамках второго подхода исследуется процесс переноса внедряемых и выбитых из узлов кристалла атомов в каскадной
- 37. Рис. 7.2 иллюстрирует разбиение по сетке энергий и углов. Обычно используется 20–100 разбиений по энергии и
- 38. 8. Метод моментов распределений Исходя из уравнения Больцмана, Линдхард с сотрудниками получил уравнение переноса для F(E,
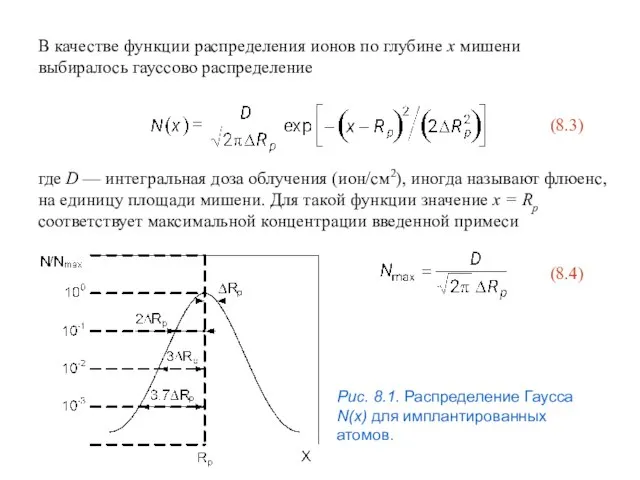
- 39. В качестве функции распределения ионов по глубине x мишени выбиралось гауссово распределение (8.3) где D —
- 40. Концентрация убывает: в два раза на глубине x ≈ Rp ± 1,2ΔRp; в десять раз x
- 41. Однако, во многих экспериментальных работах показан асимметричный (не гауссовый) вид распределений внедренных атомов. Поэтому для описания
- 42. Интегралы от вводимых функций по всему пространству задают их нормировку и поясняют их физический смысл. Функция
- 43. где — косинус угла между направлением влета ионов в мишень и направлением на рассматриваемую точку .
- 44. Соответствующие величины будем обозначать и — по аналогии со средним проективным пробегом. В наших таблицах параметров
- 45. Из-за цилиндрической симметрии нечетные степени при усреднении дают 0. Моменты второго порядка непосредственно связаны со среднеквадратичными
- 46. Смешанный момент третьего порядка типа определяет смешанную асимметрию Момент третьего порядка по X связан с продольной
- 47. Момент четвертого порядка по продольной координате x определяет эксцесс глубинного распределения (8.18) Для построения двух- и
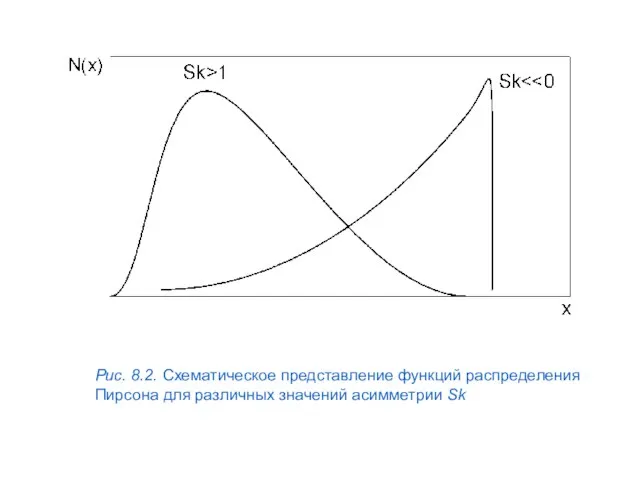
- 48. Рис. 8.2. Схематическое представление функций распределения Пирсона для различных значений асимметрии Sk
- 49. Для построения таких асимметричных профилей в наших работах применена функция Пирсона 4-го типа: Здесь K —
- 50. Здесь, как и ранее, D — доза внедряемых ионов, ион/см2. Концентрация примеси выразится в атомах на
- 51. Профиль распределения выделенной в упругих соударениях энергии (профиль радиационной поврежденности) также можно построить на основе распределения
- 52. Профиль первичных радиационных повреждений получим, разделив FD(x) на удвоенную энергию смещения Ed атома мишени из узла
- 53. Сравнивая средние глубины залегания примеси Rp со средней глубиной радиационно-поврежденного слоя RpD при ионной имплантации (см.
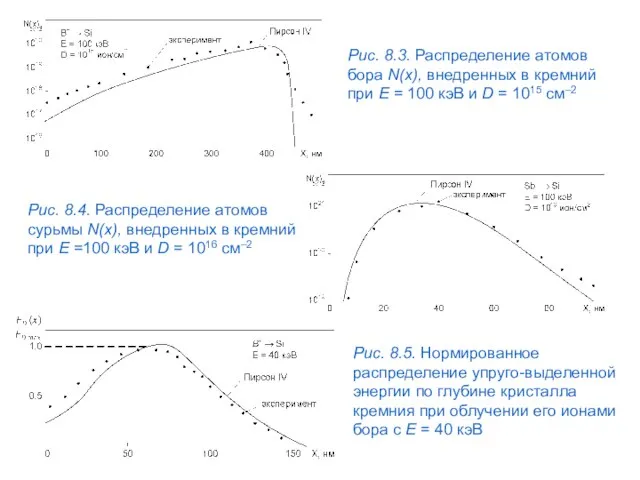
- 54. Рис. 8.3. Распределение атомов бора N(x), внедренных в кремний при E = 100 кэВ и D
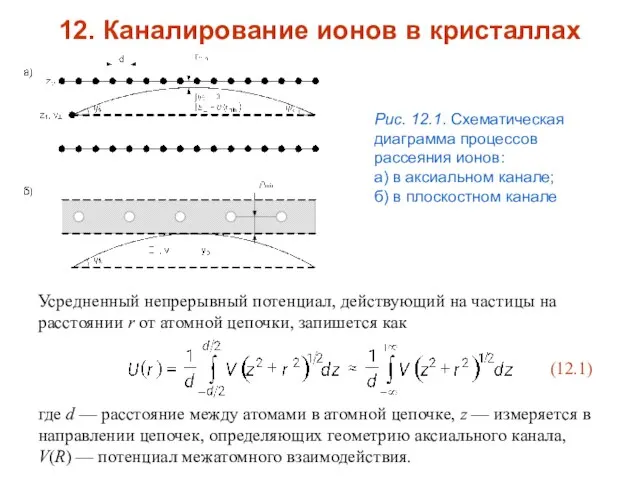
- 55. где d — расстояние между атомами в атомной цепочке, z — измеряется в направлении цепочек, определяющих
- 56. С учетом стандартного потенциала Линдхарда (4.20) для V(R) непрерывный потенциал цепочки примет вид: (12.2) где a
- 57. Приравнивая теперь E⊥ к потенциалу U(R) или U(y), можно рассчитать минимальное расстояние rmin или ρmin, на
- 58. Аналогично при плоскостном каналировании получим (12.8) Величина ψK зависит от энергии ионов и атомных номеров z1
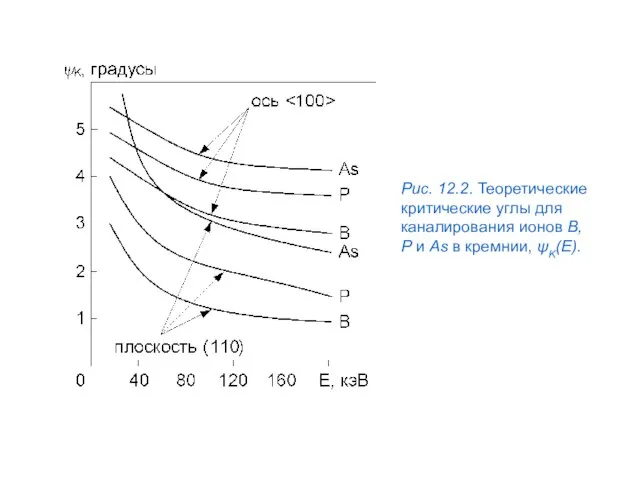
- 59. Рис. 12.2. Теоретические критические углы для каналирования ионов B, P и As в кремнии, ψK(E).
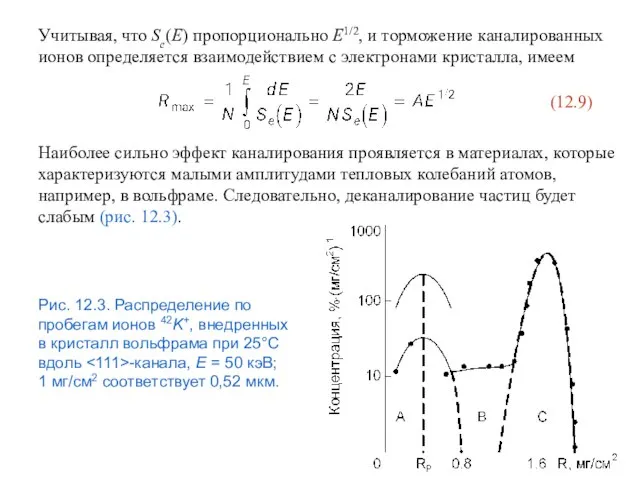
- 60. Наиболее сильно эффект каналирования проявляется в материалах, которые характеризуются малыми амплитудами тепловых колебаний атомов, например, в
- 61. Рис. 12.4. Траектории ионов при аксиальном каналировании в зависимости от положения точки входа иона относительно атомных
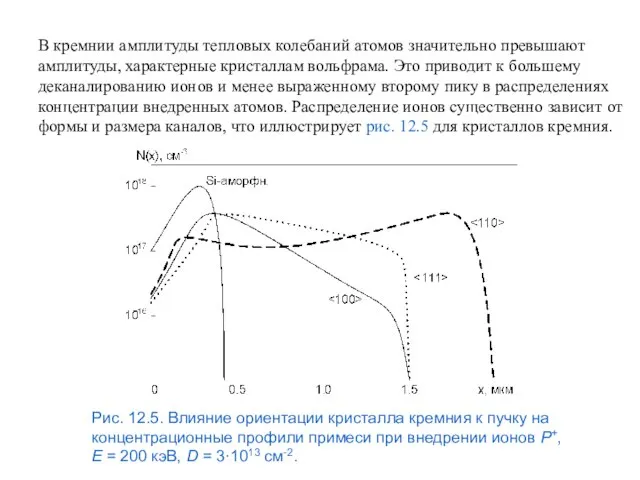
- 62. В кремнии амплитуды тепловых колебаний атомов значительно превышают амплитуды, характерные кристаллам вольфрама. Это приводит к большему
- 63. 13. Имплантация высоких доз ионов Изменение формы профиля с увеличением дозы ионов можно легко проследить теоретически
- 64. Интегрируя (13.1) с учетом (13.2) и перехода к системе координат, движущейся вместе с распыляемой поверхностью (x
- 65. При больших значениях S максимум в распределении может вообще отсутствовать, а концентрация внедренных атомов будет довольно
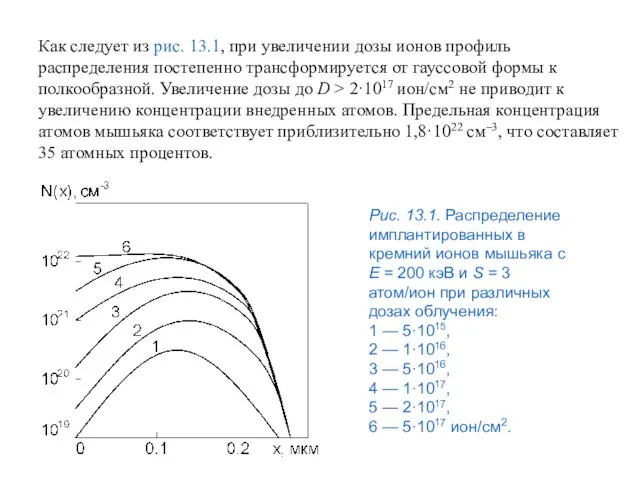
- 66. Как следует из рис. 13.1, при увеличении дозы ионов профиль распределения постепенно трансформируется от гауссовой формы
- 67. Распыление — это процесс, при котором атомы в твердом теле, лежащие близко к поверхности, получают от
- 68. где Δx — глубина, на которой переданная от иона энергия на упругие столкновения вносит вклад в
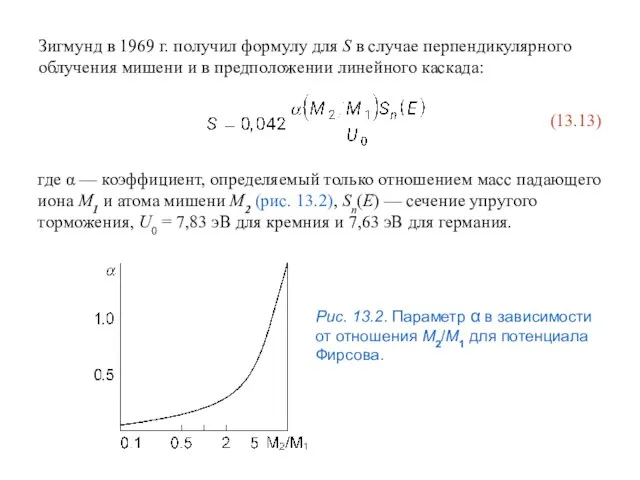
- 69. Зигмунд в 1969 г. получил формулу для S в случае перпендикулярного облучения мишени и в предположении
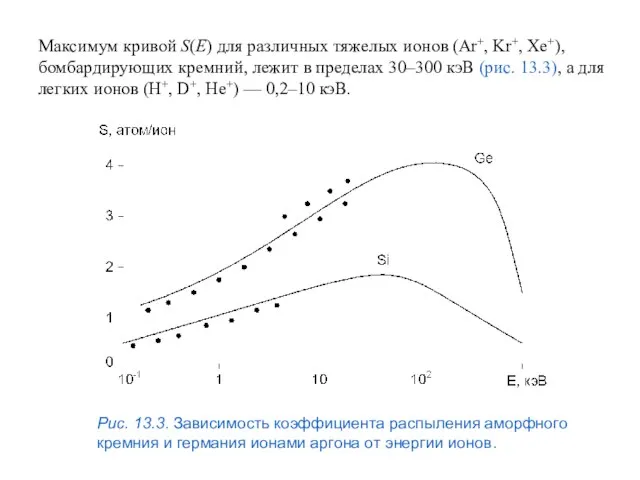
- 70. Максимум кривой S(E) для различных тяжелых ионов (Ar+, Kr+, Xe+), бомбардирующих кремний, лежит в пределах 30–300
- 71. Очень важным эффектом, часто сопутствующим ионной имплантации, наряду с таким чисто имплантационным процессом, как каналирование, является
- 72. При достаточно низких температурах, когда во время облучения нет заметной диффузии, выполняется условие: (13.21) (13.22) при
- 73. Если предположить, что коэффициент диффузии D* постоянен, т.е. не зависит от концентрации дефектов и примеси, времени
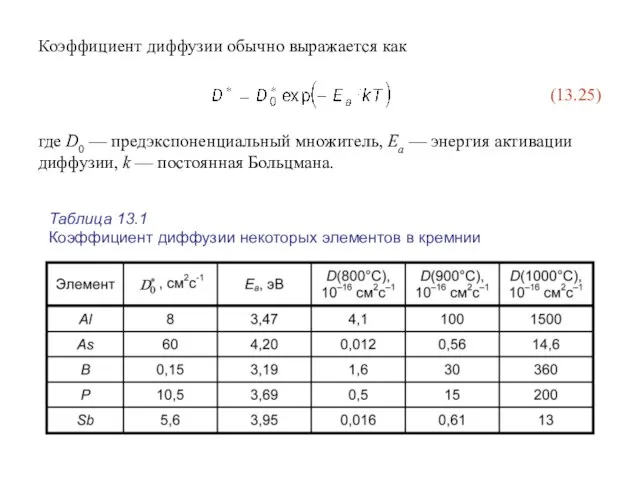
- 74. Коэффициент диффузии обычно выражается как (13.25) где D0 — предэкспоненциальный множитель, Ea — энергия активации диффузии,
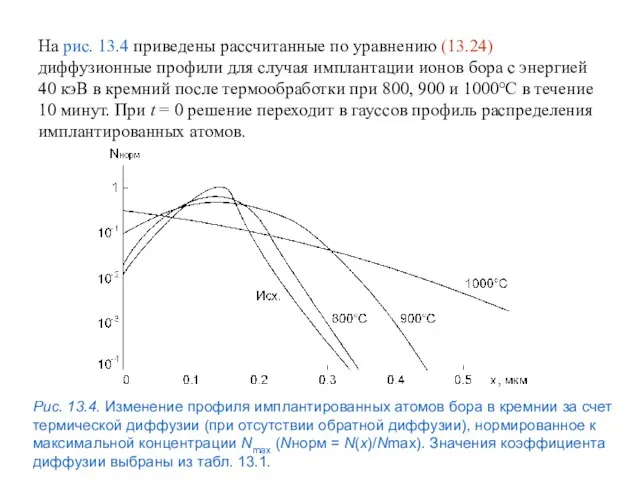
- 75. На рис. 13.4 приведены рассчитанные по уравнению (13.24) диффузионные профили для случая имплантации ионов бора с
- 76. 14. Каскады атомных смещений (14.1) где Ed — эффективная пороговая энергия смещения атома решетки. Для полупроводников
- 77. В линейных каскадах коэффициент распыления мишени линейно изменяется с ростом части энергии, выделенной в упругих столкновениях
- 78. Плотность выделенной на упругие столкновения энергии внутри каждого индивидуального каскада существенно зависит от M1, M2, E
- 79. В последующем (~10–12 с) часть дефектов ликвидируется путем спонтанной рекомбинации. Эффект спонтанной рекомбинации вакансий и междоузельных
- 81. Скачать презентацию


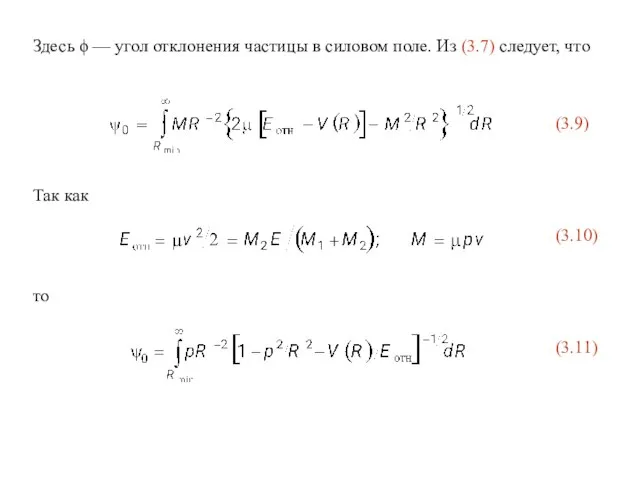























































 Київська Русь іграшка
Київська Русь іграшка Изображение человека в истории искусства
Изображение человека в истории искусства Multimedia Devices
Multimedia Devices Всероссийский съезд судей
Всероссийский съезд судей Наш друг спорт!
Наш друг спорт! Bruma Vera & Cotuc Mihaela
Bruma Vera & Cotuc Mihaela Автоматизации производственных процессов
Автоматизации производственных процессов  Особенности русского меркантилизма
Особенности русского меркантилизма ФАРМАКОЛОГИЧЕСКАЯ РЕГУЛЯЦИЯ гемостаза
ФАРМАКОЛОГИЧЕСКАЯ РЕГУЛЯЦИЯ гемостаза  Праздник Троица, обычаи и обряды
Праздник Троица, обычаи и обряды Олимпийские игры в сказочном лесу Открытый урок физкультуры во 2 классе Б МБОУ Гимназия №4 Города Новосибирска
Олимпийские игры в сказочном лесу Открытый урок физкультуры во 2 классе Б МБОУ Гимназия №4 Города Новосибирска Экономика потребителя §11
Экономика потребителя §11 Как стать налогоплательщиком налога на профессиональный доход
Как стать налогоплательщиком налога на профессиональный доход Закон Ома
Закон Ома Презентация на тему Доказательная медицина
Презентация на тему Доказательная медицина  Политические партии
Политические партии Новая книга для подростков Повесть на тему, о которой раньше молчали…
Новая книга для подростков Повесть на тему, о которой раньше молчали… Лики Чеченской войны
Лики Чеченской войны Международное гуманитарное право (МГП)
Международное гуманитарное право (МГП) АО Кокшетауские Минеральные Воды
АО Кокшетауские Минеральные Воды Производство стали
Производство стали Mayfair Developments are proud to present to you
Mayfair Developments are proud to present to you Роковой роман (М.А.Булгаков «Мастер и Маргарита»)
Роковой роман (М.А.Булгаков «Мастер и Маргарита»)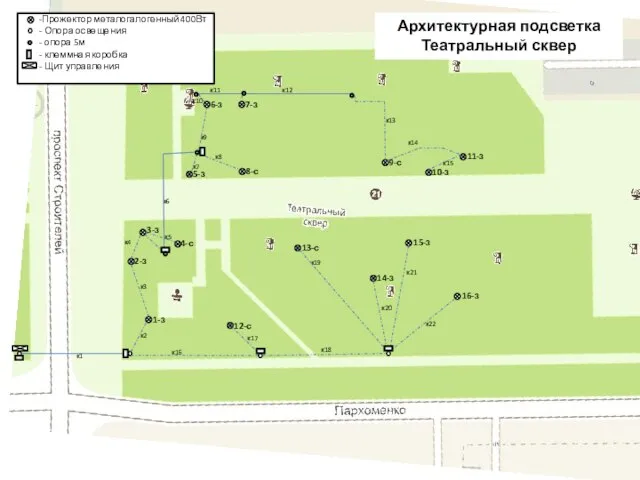 План растановки прожекторов. Архитектурная подсветка. Театральная площадь. Театральный сквер
План растановки прожекторов. Архитектурная подсветка. Театральная площадь. Театральный сквер БАЛАНС
БАЛАНС Однородные члены предложения
Однородные члены предложения Презентация на тему Портфолио (Миляхова Оксана Вячеславовна)
Презентация на тему Портфолио (Миляхова Оксана Вячеславовна)  По улицам родного города
По улицам родного города