Содержание
- 2. Элементы алгебры контактных схем
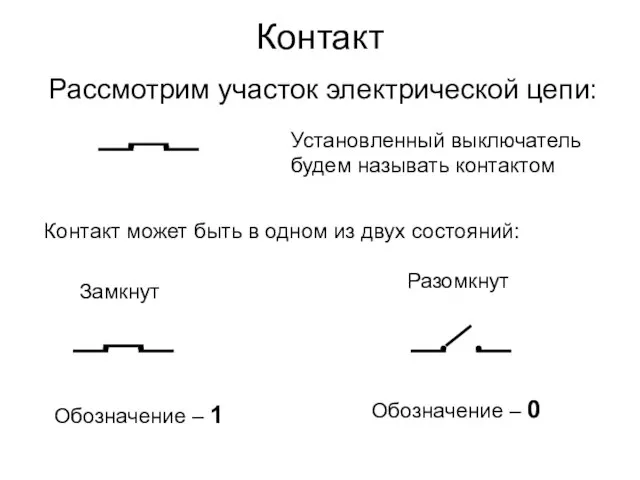
- 3. Контакт Рассмотрим участок электрической цепи: Установленный выключатель будем называть контактом Контакт может быть в одном из
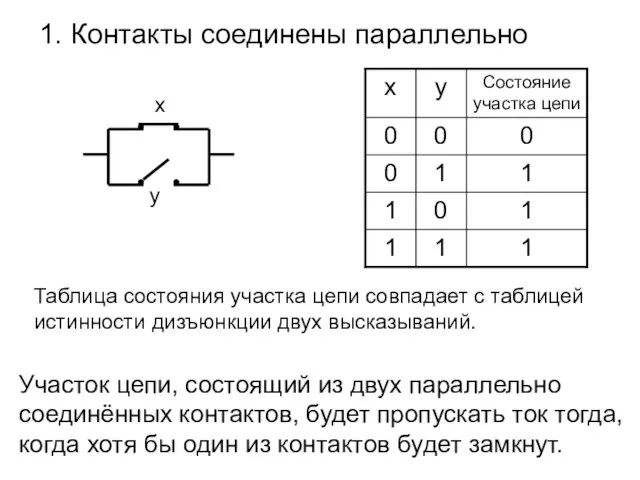
- 4. 1. Контакты соединены параллельно х Таблица состояния участка цепи совпадает с таблицей истинности дизъюнкции двух высказываний.
- 5. 2. Контакты соединены последовательно х y Таблица состояния участка цепи совпадает с таблицей истинности конъюнкции двух
- 6. 3. Электромагнитное реле Каждой контактной схеме, состоящей из параллельного, последовательного соединений, размыкающих и замыкающих контактов реле,
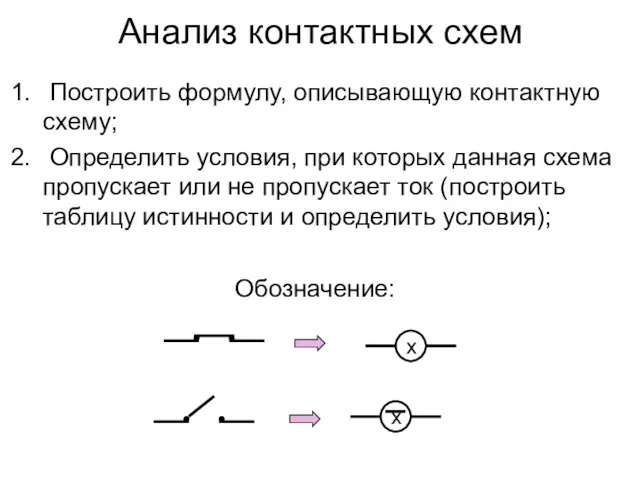
- 7. Анализ контактных схем Построить формулу, описывающую контактную схему; Определить условия, при которых данная схема пропускает или
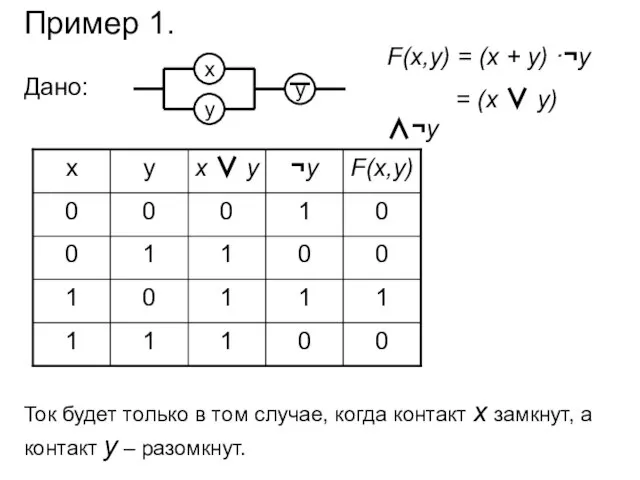
- 8. Пример 1. Дано: F(x,y) = (x + y) ·¬y = (x ∨ y) ∧¬y Ток будет
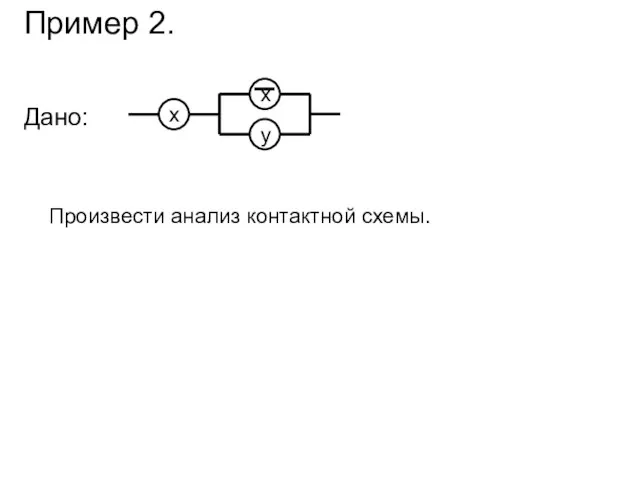
- 9. Пример 2. Дано: Произвести анализ контактной схемы.
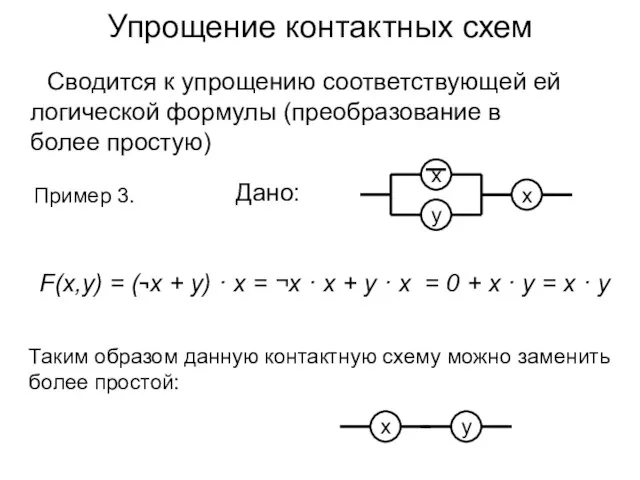
- 10. Упрощение контактных схем Сводится к упрощению соответствующей ей логической формулы (преобразование в более простую) Дано: Пример
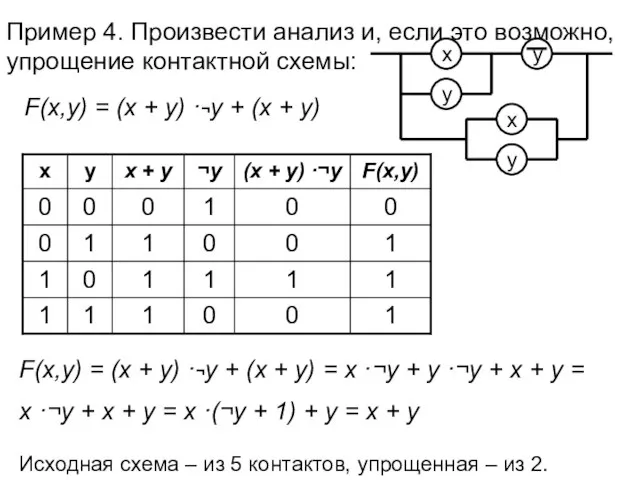
- 11. Пример 4. Произвести анализ и, если это возможно, упрощение контактной схемы: F(x,y) = (x + y)
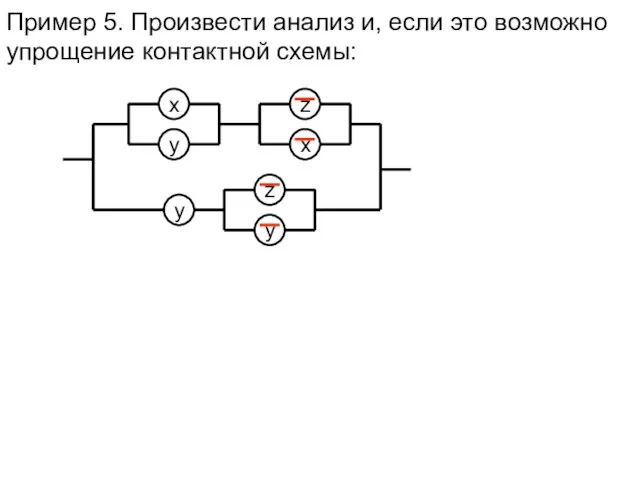
- 12. Пример 5. Произвести анализ и, если это возможно упрощение контактной схемы:
- 13. Синтез контактных схем Заключается в построении таблицы истинности по заданным условиям работы будущей схемы, в составлении
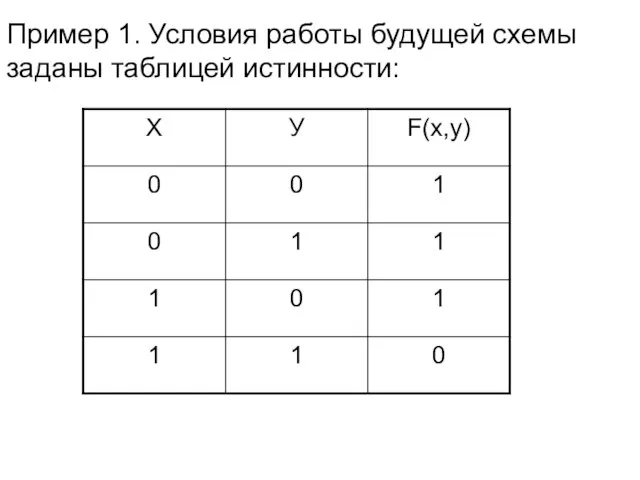
- 14. Пример 1. Условия работы будущей схемы заданы таблицей истинности:
- 15. Правило составления логической формулы по таблице истинности Для строки таблицы, где на выходе 1 записываем конъюнкцию
- 17. Скачать презентацию





 Метод фокальных объектов
Метод фокальных объектов ДОМЕННЫЕ ВОЙНЫ ПО-УКРАИНСКИ
ДОМЕННЫЕ ВОЙНЫ ПО-УКРАИНСКИ Продукция: Икра
Продукция: Икра Проблемно-поисковые образовательные технологии проблемное обучение метод проектов «мозговой штурм»
Проблемно-поисковые образовательные технологии проблемное обучение метод проектов «мозговой штурм» Конфликт и пути его решения
Конфликт и пути его решения Защита персональных данных в СКПК Председатель ВОСПКК «Вологда-Кредит» Петухова Надежда, к.э.н.14- 16 марта 2012 годаКонференци
Защита персональных данных в СКПК Председатель ВОСПКК «Вологда-Кредит» Петухова Надежда, к.э.н.14- 16 марта 2012 годаКонференци Банковское дело. Самарский Государственный Экономический Университет
Банковское дело. Самарский Государственный Экономический Университет Театр уж полон… Ложи блещут…
Театр уж полон… Ложи блещут… Инновативные технологии и цифровые трансформации в высшем образовании
Инновативные технологии и цифровые трансформации в высшем образовании Зрительные иллюзии
Зрительные иллюзии Актуальные вопросы функционирования розничных рынков электроэнергии
Актуальные вопросы функционирования розничных рынков электроэнергии Психологические особенности подросткового возраста
Психологические особенности подросткового возраста Презентация на тему Автомобильные семейки
Презентация на тему Автомобильные семейки  Женские образы в творчестве художников
Женские образы в творчестве художников Погода
Погода Intel
Intel Презентация на тему Моделирование ввода данных, разработка экспериментальных прогонов программы и её проверка
Презентация на тему Моделирование ввода данных, разработка экспериментальных прогонов программы и её проверка История русской одежды
История русской одежды Примеры постановки цели реализации целеполагания в компаниях, производящих газировку и соки
Примеры постановки цели реализации целеполагания в компаниях, производящих газировку и соки МОУ «Кужмарская средняя общеобразовательная школа» Звениговского района Республики Марий Эл
МОУ «Кужмарская средняя общеобразовательная школа» Звениговского района Республики Марий Эл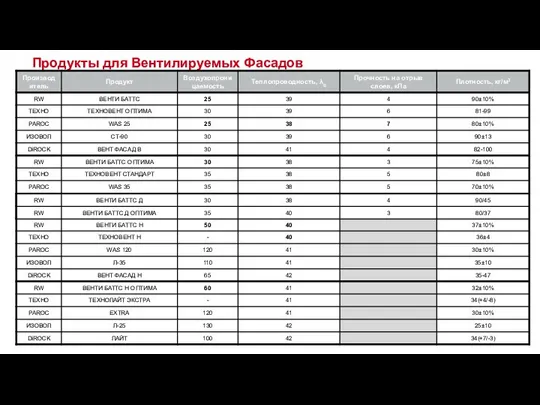 Продукты для Вентилируемых Фасадов
Продукты для Вентилируемых Фасадов Электронные образовательные ресурсы.Практика применения в учебно-воспитательном процессе
Электронные образовательные ресурсы.Практика применения в учебно-воспитательном процессе Индукционный лаг ИЭЛ-2М
Индукционный лаг ИЭЛ-2М Развитие рынка SaaS решений в телекоме
Развитие рынка SaaS решений в телекоме Компания ЧТУП БелТоргХолод поставщик торгового и технологического оборудования для компаний в сегменте Фаст-фуд
Компания ЧТУП БелТоргХолод поставщик торгового и технологического оборудования для компаний в сегменте Фаст-фуд Клубный час Как вести себя за столом? Основы столового этикета
Клубный час Как вести себя за столом? Основы столового этикета ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО П
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО П Совет сторонников Всероссийской политической партии Единая Россия Миасского городского округа. Моя любимая работа
Совет сторонников Всероссийской политической партии Единая Россия Миасского городского округа. Моя любимая работа