Формулы сокращенного умножения

Оглавление
Вокруг квадрата суммы
Небольшой рассказ про формулу
Формула полного квадрата
Вокруг куба суммы
Лжецы и рыцари (шуточная задача)
Вокруг разности квадратов
«краткий курс японского языка»
(шуточная головоломка)

Вокруг квадрата суммы
Новые сапоги всегда жмут.

Что такое формула?
Формулой
называется символьная запись, содержащая некоторые утверждения
Рассмотрим пример

Рассмотрим пример
Найдите квадрат двучлена
aa+a+b

Ответ
Начнем сначала: в этом задании вы встретились с тождеством
(a+b)² = a² + 2ab + b²
С точки зрения понятия формулы наше тождество содержит как минимум две формулы.
Первая формула (a+b)² = a² + 2ab + b² утверждает, что квадрат двучлена можно найти, не умножая каждый раз (a+b) на (a+b), а более приятным путем

Формула квадрата суммы
Ее вид
Ее имя
Ее прочтение
Ее схема

Вид формулы
(a+b)² = a² + 2ab + b²

Имя формулы
Формула квадрата суммы
Оно дано по виду левой части равенства.

Прочтение формулы
Квадрат суммы двух алгебраических выражений равен квадрату первого слагаемого плюс удвоенное произведение первого слагаемого на второе плюс квадрат второго слагаемого.

Схема формулы
( + )² = ² + 2 + 2
- b
- a

На основе этой формулы основаны формулы квадрата разности и квадрата трехчлена.
Квадрат разности
(a – b)² = a² - 2ab + b²
Квадрат трехчлена
(a + b + с)² = a² + b² + c² +2ab + 2bc + 2ac

Небольшой рассказ про формулу
Эту формулу усердно зубрили многие поколения школьников. Приведем отрывок из книги Б.Нушича.
- Где ты родился, Спира? – спрашивает учитель математики Спиру Найдановича.
Спира молчит, хлопает глазами и смотрит в потолок.
- Где ты родился, Спира? – повторяет учитель.
Спира молчит, хлопает глазами и смотрит в потолок.
- Бог ты мой, ты что, не знаешь, где родился?
- Я забыл.
- А что ты еще знаешь? Ну, скажи мне, что ты знаешь, если ты даже не знаешь, где родился?
-А плюс В в квадрате равно А в квадрате плюс два АВ плюс В в квадрате, - выпалил Спира, как из пулемета.

Знакомимся с формулой полного квадрата

Реши уравнение
(x + 3,5)² = 0
При решении уравнений
и при вычислений значений
выражений вы встретили выражение
a² ± 2 ab + b²

Это выражение называется формулой
ПОЛНОГО КВАДРАТА
Ее вид
Ее имя
Ее схема

Вид формулы
a² ± 2ab + b²

Имя формулы
ФОРМУЛА ПОЛНОГО КВАДРАТА

Схема формулы
² ± 2 + ² = ( ± )²
- это a
- это b

ВОКРУГ КУБА СУММЫ
Что есть лучшего? –
Сравнив прошедшее,
Свести его настоящим.

Рассмотри пример
Возведите в куб двучлен
aa+a+b

Это выражение решается таким образом
(a + b)³ = a³ + 3a²b + 3ab² + b³
Это формула куба суммы.
Из этой формулы можно создать аналогичную формулу куба разности
(a - b)³ = a³ - 3a²b + 3ab² - b³
нажмите

Это
ФОРМУЛЫ ПОЛНОГО КУБА
так называют их по аналогии с формулами полного квадрата

Лжецы и рыцари
(шуточная задача)
Предположим, вы попали на остров, жители которого делятся на две группы: группу рыцарей, всегда говорящих правду, и группу лжецов, говорящих только ложь... И вам при разговоре с островитянами всякий раз придется определять, верить ответу или нет.
Вы встречаете троих жителей острова: А, В и С. Желая выяснить, кто из них рыцарь, а кто лжец, вы задаете им вопросы.
Вопрос к А:
- Вы рыцарь или лжец?
А говорит что-то очень неразборчиво.
Вопрос к В:
- Что сказал А?
В:
- А сказал, что он лжец.
С:
- Не верьте В! В – лжец!
Ответ

Ответ
Ни рыцарь, ни лжец не могут сказать: «Я лжец» (высказав подобное утверждение, рыцарь солгал бы, а лжец изрек бы истину).
Следовательно, A, кем бы он ни был, не мог сказать о себе, что он лжец. Поэтому B, утверждая, будто A назвал себя лжецом, заведомо лгал. Значит, B – лжец. Так сказал С сказал, что B лгал, то С изрек истину. Следовательно С – рыцарь.
Таким образом B – лжец, а С – рыцарь. (Установить, кем был A, не представляется возможным).

Вокруг разности квадратов
Бросая в воду камешки,
смотри на круги,
ими образуемые;
иначе такое бросание
будет пустою забавою.

Выполните умножение
(2х + 3у) (2х +3у);
(3 - аb²) (3a - b²);
(z2 + z +2) (z + 2);
(а + b) (a – b);
(2a – 5) (2a – 5)2 ;
Оцените свою работу так:
11балов, если все примеры выполнялись только по правилу умножения многочленов;
(11 + п) баллов, где п – число произведений, которые вы нашли, используя формулы сокращенного умножения.
Умножив (a + b) на (a – b), вы тем самым доказали тождество
((a + b)(a + b)((a + b)(a – b)(a + b)(a – b) = (a + b)(a – b) = a² - b²

(a + b)(a – b) = a² - b²
Это выражение является
ФОРМУЛОЙ ПРОИЗВЕДЕНИЙ СУММЫ НА РАЗНОСТЬ
Ее прочтение
Ее схема

Прочтение формулы
Произведение суммы алгебраических выражений на их разность равно разности квадратов этих алгебраических выражений

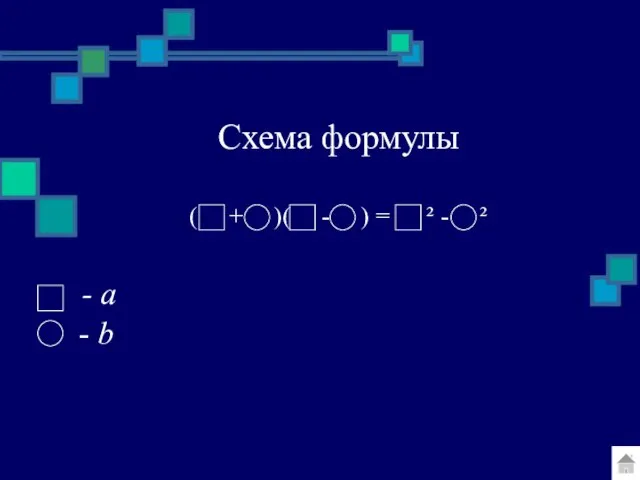
Схема формулы
( + )( - ) = ² - ²
- a
- b

«краткий курс японского языка»
(шуточная головоломка)
Даны фразы на японском языке с переводом на русский язык
1. Анохито-ва хон-о ёндэ нику-о табэта.
Он прочел книгу и съел мясо.
2. Сэйто-ва сюкудай-о манадэ хон-о ёндэ юсеку-о табэру.
Ученик выучит уроки, прочтет книгу и съест ужин.
3. Сэйто-ва мидзу-о нондэ дзасси-о акэта.
Ученик выпил воду и открыл журнал.
4. Анохито-ва то-то мадо-о акэтэ симбун-о ему.
Он откроет дверь и окно и прочитает газету.
5.Ину-ва хонэ-о каму.
Собака сгрызет кость.
6. Анохито-ва хон-то дзасси-о катаесэтэ цую-о нонда.
Он отложил книгу и журнал и выпил сок.
7. Мисуко-ва сюкудай-о катаесэру
Сын отложит уроки.
Переведи на японский язык:
1. Ученик откроет журнал и газету.
2. Он съел ужин и выучил уроки.
3. Собака сгрызет кость и выпьет воду

Сэйто-ва дзасси-о акэта ему

Анохито-ва нику-о табэру сюкудай-о манадэ