Содержание
- 2. «…подготовка к ЕГЭ стала сегодня основной целью работы учителя. А результаты ЕГЭ – основным мерилом его
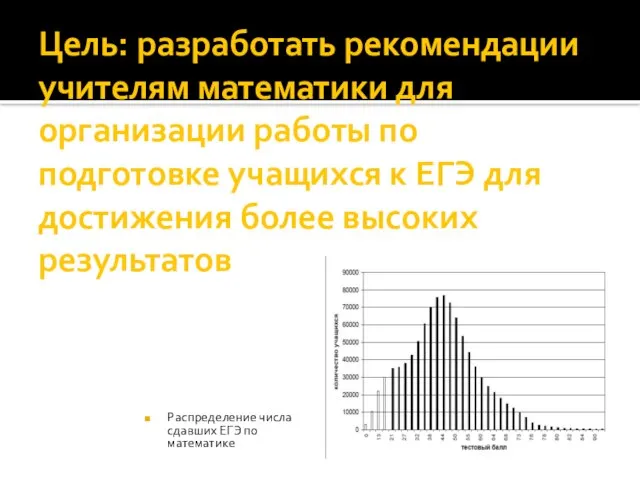
- 3. Цель: разработать рекомендации учителям математики для организации работы по подготовке учащихся к ЕГЭ для достижения более
- 4. Задачи: Проанализировать основные ошибки учащихся, допускаемые при выполнении КИМов ЕГЭ по математике, при этом найти наиболее
- 5. Основные трудности при подготовке учащихся к ЕГЭ Непредсказуемость содержания заданий ЕГЭ; Нетипичность и многообразие формулировок заданий
- 6. Основные трудности при подготовке учащихся к ЕГЭ Организация и планирование работы по подготовке учащихся к ЕГЭ
- 7. Педагогическая система подготовки учащихся к ЕГЭ по математике Подготовительный этап Практический этап Диагностический этап
- 8. Наиболее проблемные темы математики (по алгебре и началам анализа): 1. Свойства корня степени n. 2. Свойства
- 9. Наиболее проблемные темы математики (по геометрии): 1. Признаки равенства и подобия треугольников. 2. Решение треугольников. 3.
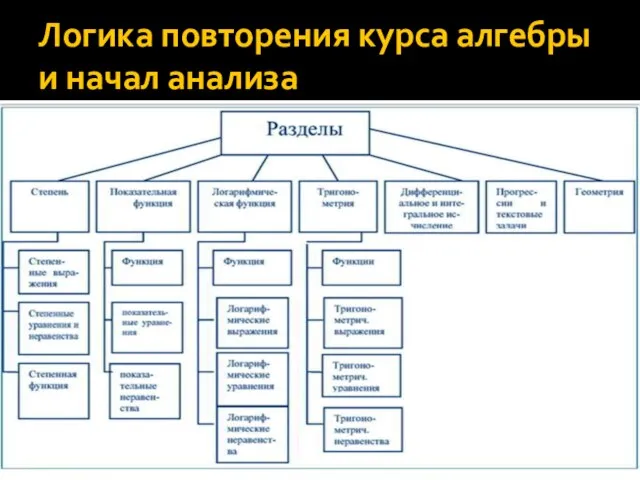
- 10. Логика повторения курса алгебры и начал анализа
- 11. Методы работы с тестами. Необходимо: внедрять в учебный процесс разноуровневые тематические тесты; обратить внимание на формулировки
- 12. Контроль как метод установления обратной связи «Чем интенсивнее и качественнее контроль, тем больше условий и возможностей
- 13. Для того чтобы узнать, как усвоили учащиеся тот или иной материал и не допустить пробелов в
- 14. Психологические аспекты подготовки к ЕГЭ
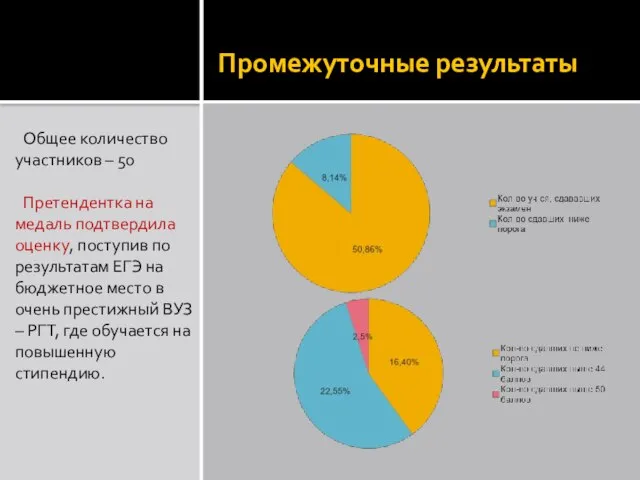
- 15. Промежуточные результаты Общее количество участников – 50 Претендентка на медаль подтвердила оценку, поступив по результатам ЕГЭ
- 16. Анализ ошибок: По уровню освоения учебных тем вызывают серьёзные затруднения свойства функций, решение логарифмических неравенств, решение
- 17. ЗАКЛЮЧЕНИЕ необходимо совершенствовать процесс преподавания: активнее включать в учебный процесс идеи дифференцированного обучения (дифференциация требований в
- 18. ЗАКЛЮЧЕНИЕ
- 19. СПАСИБО ЗА ВНИМАНИЕ
- 20. Ваше участие в итоговой атттестации!. А)готовлю учащихся к выпускным экзаменам Б) классный руководитель выпускного класса В)
- 21. 2. Ваше отношение к новой форме проведения итоговой аттестации А) приветствую Б) принимаю В) мне все
- 22. 3. Считаете ли Вы, что ЕГЭ и ГИА проверяют знания учащихся А) безусловно Б) частично В)
- 23. 4. КИМЫ А) соответствуют школьной программе Б) составлены корректно В) условия некоторых заданий составлены не корректно
- 25. Скачать презентацию



















 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут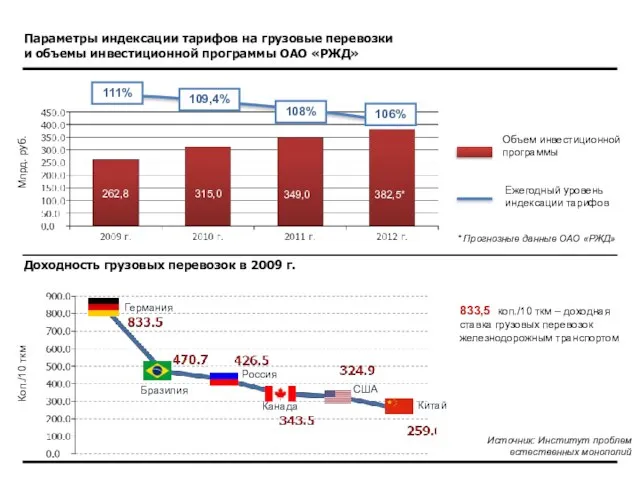 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе