Содержание
- 2. Функция – одно из основных математических и общенаучных понятий. Оно играет БОЛЬШУЮ роль в познании реального
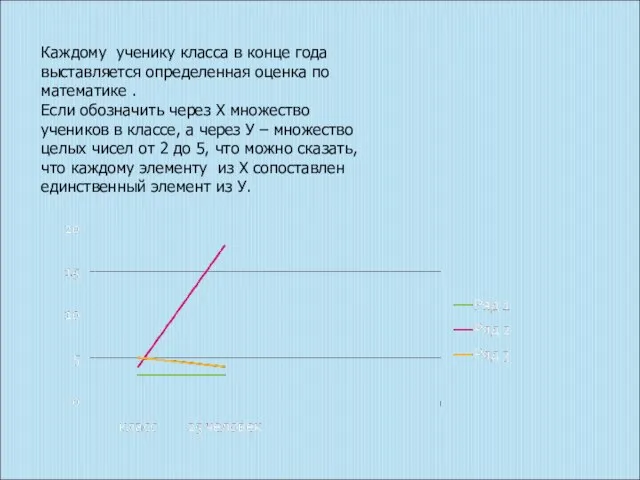
- 3. Каждому ученику класса в конце года выставляется определенная оценка по математике . Если обозначить через Х
- 4. Идея функциональной зависимости восходит к древности. Её содержание обнаруживается уже в первых математических выраженных соотношения между
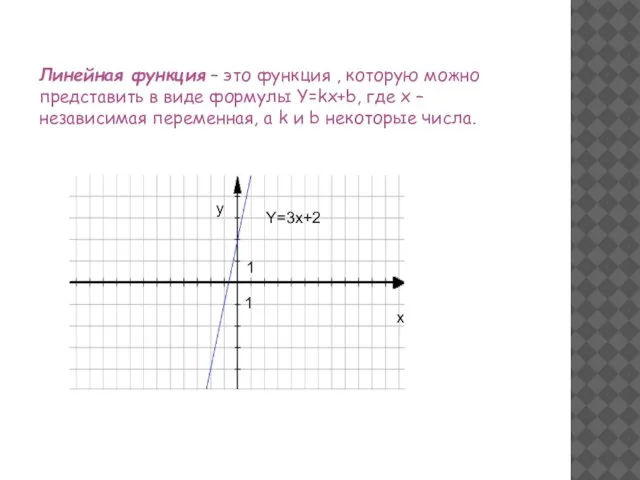
- 5. Линейная функция – это функция , которую можно представить в виде формулы Y=kx+b, где х –
- 6. Прямая графика линейной функции пересекает ось ординат в точке (0; b), А ось абсцисс в точке
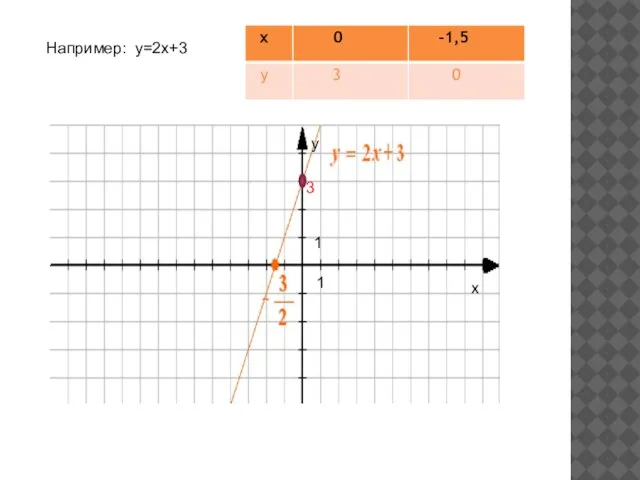
- 7. Например: y=2x+3 x y 1 1 3
- 8. Прямой пропорциональностью называется функция, которую можно задать формулой вида y=kx, где x – независимая переменная k
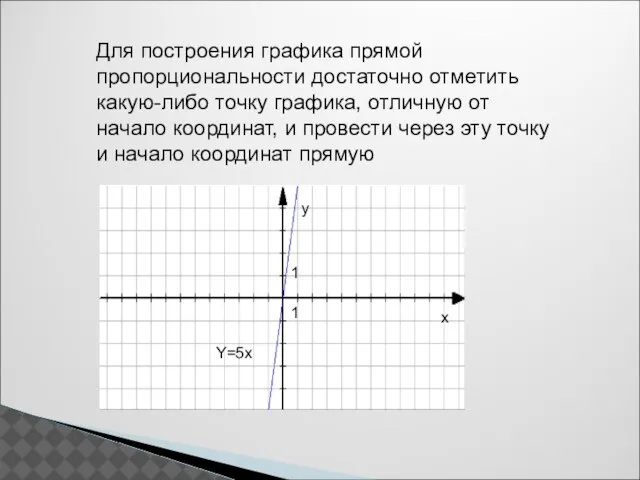
- 9. Для построения графика прямой пропорциональности достаточно отметить какую-либо точку графика, отличную от начало координат, и провести
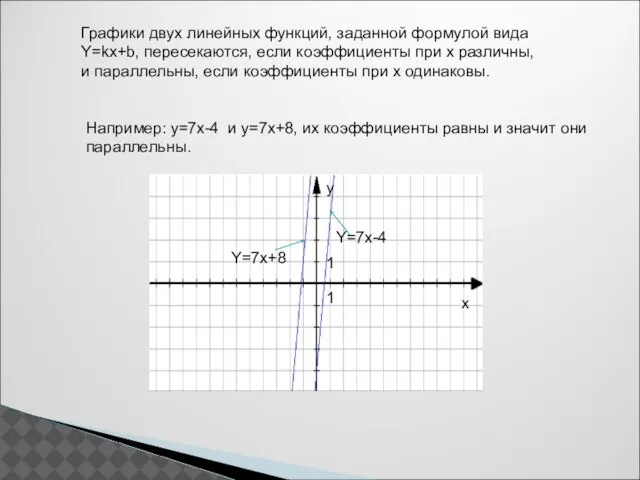
- 10. Графики двух линейных функций, заданной формулой вида Y=kx+b, пересекаются, если коэффициенты при x различны, и параллельны,
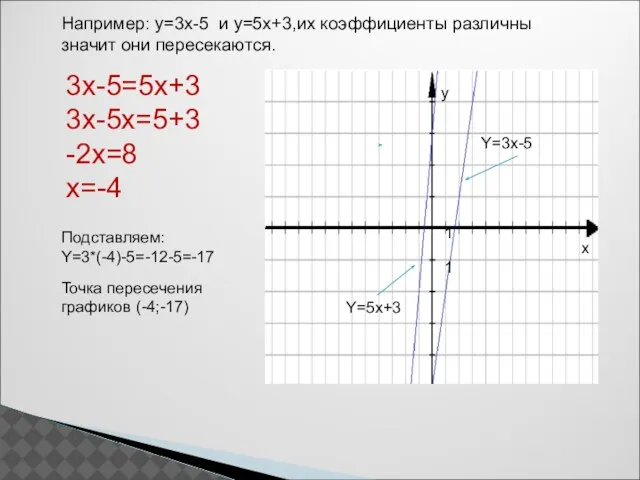
- 11. Например: y=3x-5 и y=5x+3,их коэффициенты различны значит они пересекаются. 3x-5=5x+3 3x-5x=5+3 -2x=8 x=-4 Подставляем: Y=3*(-4)-5=-12-5=-17 Точка
- 13. Скачать презентацию



 Координатная плоскость
Координатная плоскость СМП при кровотечениях
СМП при кровотечениях СПИД - наиболее опасное инфекционное заболевание.
СПИД - наиболее опасное инфекционное заболевание. ШУКШИН Василий Макарович (1927—1974), русский писатель, кинорежиссер, актер
ШУКШИН Василий Макарович (1927—1974), русский писатель, кинорежиссер, актер The computers in our life
The computers in our life ВОСПИТАТЕЛЬ: ТОЛМАЧЕВА РАИСА АНДРЕЕВНА ВОСПИТАТЕЛЬ: ГАЙДУК ОЛЬГА АЛЕКСАНДРОВНА.
ВОСПИТАТЕЛЬ: ТОЛМАЧЕВА РАИСА АНДРЕЕВНА ВОСПИТАТЕЛЬ: ГАЙДУК ОЛЬГА АЛЕКСАНДРОВНА. Национальная Интегрированная Информационная система Здравоохранения Республики Узбекистан
Национальная Интегрированная Информационная система Здравоохранения Республики Узбекистан Экономическое устройство России
Экономическое устройство России Гиподинамия
Гиподинамия Цифроаналоговые преобразователи
Цифроаналоговые преобразователи Динамика процентных выплат
Динамика процентных выплат Муниципальное дошкольное образовательное учреждение Старомазинский детский сад «Солнышко»
Муниципальное дошкольное образовательное учреждение Старомазинский детский сад «Солнышко» Русские народные праздники
Русские народные праздники Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии
Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии Замена старых оконных рам в библиотеке
Замена старых оконных рам в библиотеке ГОСУДАРСТВЕННОЕ УСТРОЙСТВО СОВРЕМЕННОЙ РОССИИ.Урок-практика.
ГОСУДАРСТВЕННОЕ УСТРОЙСТВО СОВРЕМЕННОЙ РОССИИ.Урок-практика. Итоги деятельности АОГидропроект за 2018 год
Итоги деятельности АОГидропроект за 2018 год Презентация на тему Мышечная деятельность
Презентация на тему Мышечная деятельность Информация и знания
Информация и знания УЧЕБНЫЕ ПРОГРАММЫ ДОПОЛНИТЕЛЬНЫХ ПЛАТНЫХ ОБРАЗОВАТЕЛЬНЫХ УСЛУГ:МОНИТОРИНГ КАЧЕСТВА
УЧЕБНЫЕ ПРОГРАММЫ ДОПОЛНИТЕЛЬНЫХ ПЛАТНЫХ ОБРАЗОВАТЕЛЬНЫХ УСЛУГ:МОНИТОРИНГ КАЧЕСТВА Коммерческое предложение. Оптовая торговля овощей
Коммерческое предложение. Оптовая торговля овощей Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Правила пожарной безопасности
Правила пожарной безопасности Обзор социальных сетей и продвижения в них
Обзор социальных сетей и продвижения в них Бампербол - футбол в шарах
Бампербол - футбол в шарах Обзорная лекция по формированию и развитию управления в РФ
Обзорная лекция по формированию и развитию управления в РФ «Анализ готовности школы к введению ФГОС второго поколения»
«Анализ готовности школы к введению ФГОС второго поколения» Презентация
Презентация