Функция арифметического квадратного корня

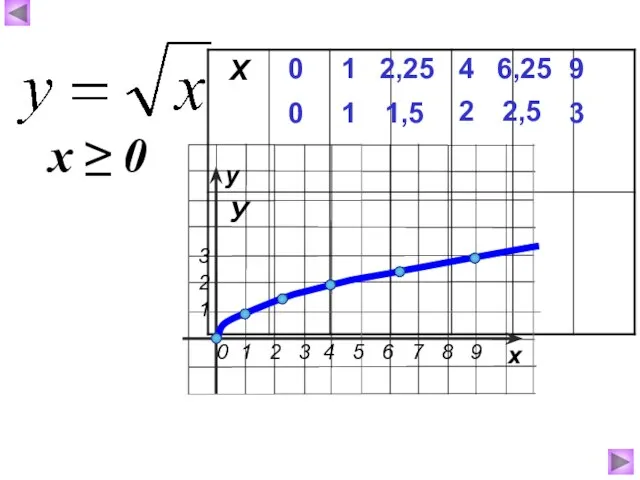
0
0
1
1
4
2
6,25
2,5
9
3
2,25
1,5
х ≥ 0

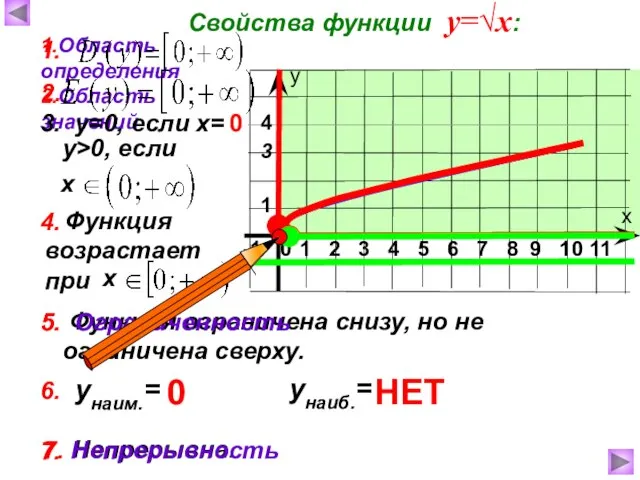
7.
Непрерывна.
Функция возрастает при
Функция ограничена снизу, но не ограничена сверху.
Свойства функции у=√х:
1.Область определения
2.Область значений
3. у=0, если х=
0
у>0, если
4.
5. Ограниченность
1.
2.
5.
6. унаим.=
унаиб.=
НЕТ
0
7. Непрерывность

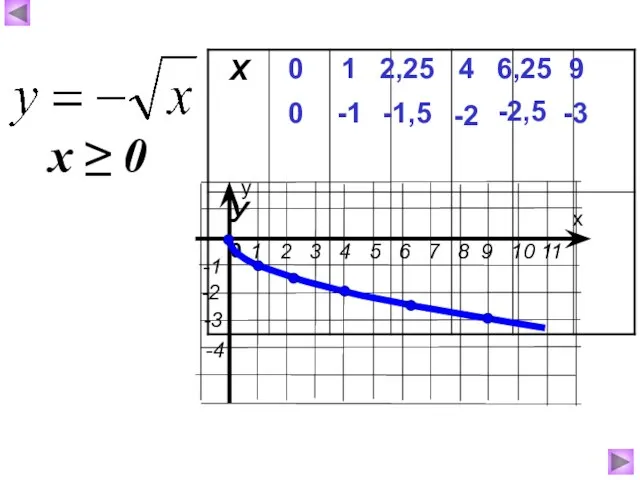
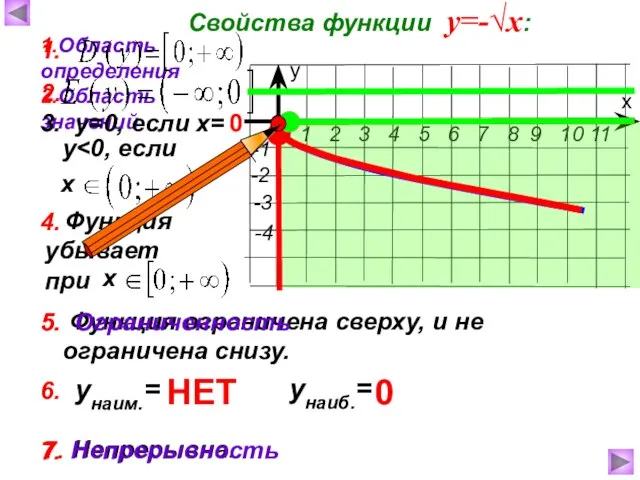
0
0
1
-1
4
-2
6,25
-2,5
9
-3
2,25
-1,5
х ≥ 0

7.
Непрерывна.
Функция убывает при
Функция ограничена сверху, и не ограничена снизу.
Свойства функции у=-√х:
1.Область определения
2.Область значений
3. у=0, если х=
0
у<0, если
4.
5. Ограниченность
1.
2.
5.
6. унаим.=
унаиб.=
0
НЕТ
7. Непрерывность

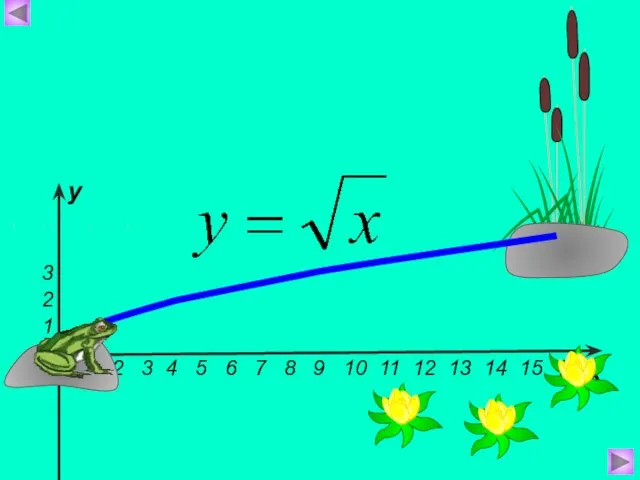
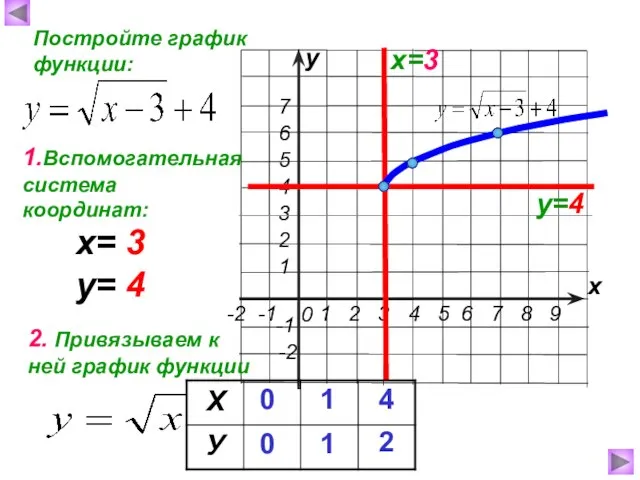
х
у
Постройте график функции:
х=3
у=4
1.Вспомогательная система координат:
2. Привязываем к ней график функции
х= 3
у= 4
0
0
1
1
4
2

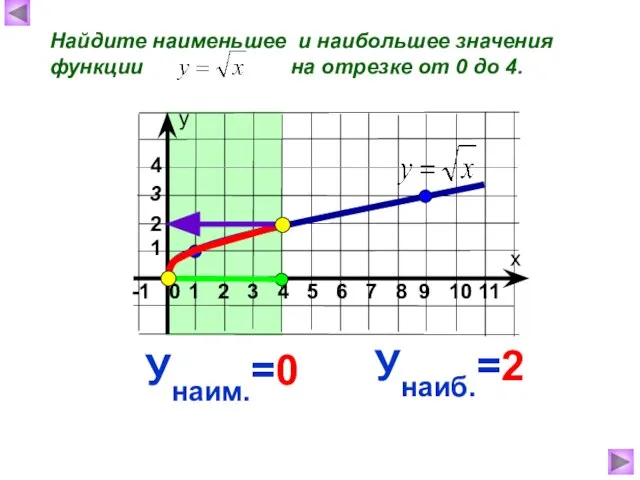
Найдите наименьшее и наибольшее значения функции на отрезке от 0 до 4.
Унаиб.=2
Унаим.=0
2

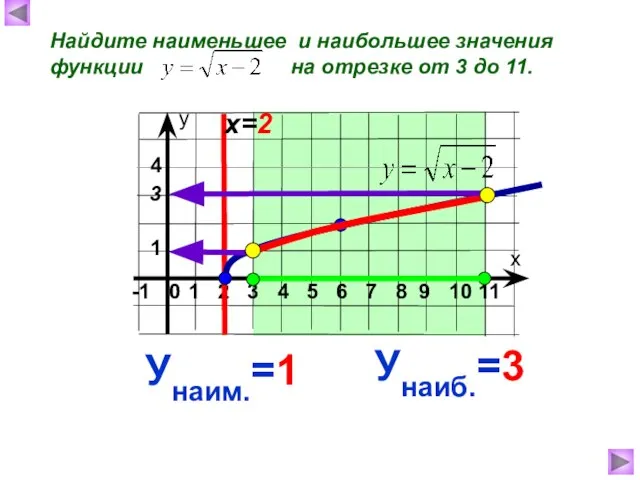
Найдите наименьшее и наибольшее значения функции на отрезке от 3 до 11.
х=2
Унаиб.=3
Унаим.=1

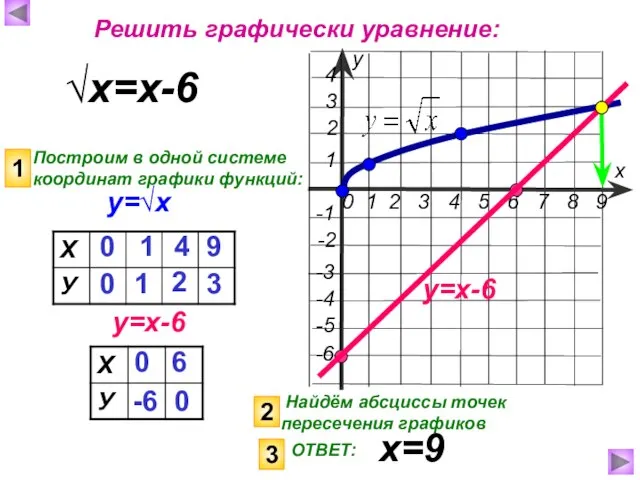
у=√х
√х=х-6
Построим в одной системе координат графики функций:
у=х-6
1
0
-6
6
0
2
Найдём абсциссы точек пересечения графиков
3
ОТВЕТ:
х=9
Решить графически уравнение:
у=х-6
0
0
1
1
4
9
2
3

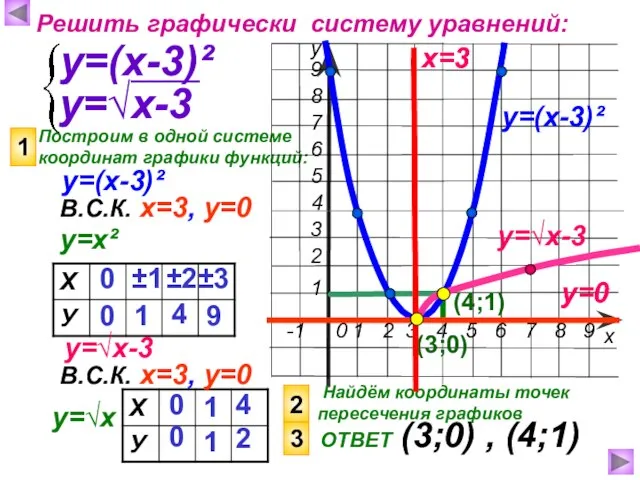
Построим в одной системе координат графики функций:
х
у
Решить графически систему уравнений:
у=(х-3)²
у=(х-3)²
1
у=(х-3)²
у=√х-3
Найдём координаты точек пересечения графиков
ОТВЕТ
(3;0) , (4;1)
х=3
у=0
(3;0)
0
0
±1
1
±2
±3
4
9
у=х²
В.С.К. х=3, у=0
0
0
1
4
2
В.С.К. х=3, у=0
у=√х
1
(4;1)
х=3
у=0
у=√х-3
2
3

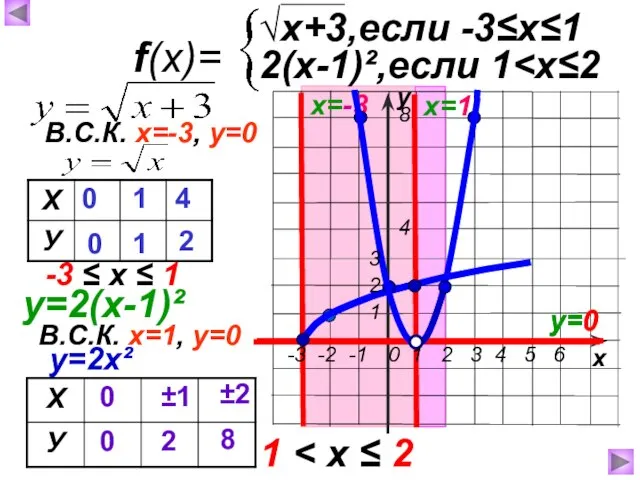
f(x)=
Постройте график функции
и опишите её свойства.
√x+3,если -3≤х≤1
2(х-1)²,если 1<х≤2

у
х
f(x)=
√x+3,если -3≤х≤1
2(х-1)²,если 1<х≤2
х=-3
0
0
1
1
4
2
В.С.К. х=-3, у=0
у=0
у=2(х-1)²
-3 ≤ х ≤ 1
В.С.К. х=1, у=0
х=1
у=0
у=2х²
0
0
±1
2
±2
8
1 < х ≤ 2