Содержание
- 3. Многопрофильная гимназия №79 ОТКРЫТЫЙ УРОК «ГЕОМЕТРИЧЕСКАЯ ПИРАМИДА И ЕЁ ПРОЕКЦИЯ» Учитель: Волкова Лидия Николаевна 2009г. Город
- 4. Презентацию готовили Дасиева Роза, Набоко Михаил, Ибрагимова Карина, Егизбаева Айнура, Асанова Эльвира, Ускенбаева Мадия.
- 5. О слове пирамида. Пирамида. Слово «пирамида» в геометрию ввели греки, которые, как полагают, заимствовали его у
- 6. Пирамида- многогранник, у которого основание- многоугольник, боковые грани- треугольники, имеющие общую вершину. Что же такое пирамида?
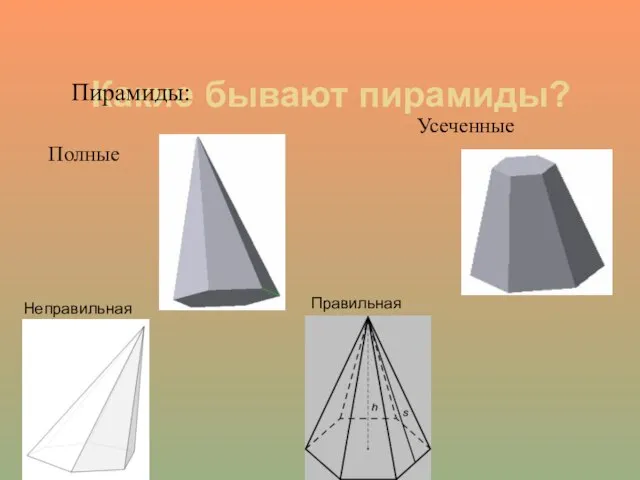
- 7. Какие бывают пирамиды? Пирамиды: Полные Усеченные Неправильная Правильная
- 8. От чего зависит вид пирамиды? Вид пирамиды зависит от многоугольника, который лежит в основании.
- 9. Проекция пирамиды Пирамида треугольная
- 11. О полной (не усечённой) пирамиде.
- 12. Пирамида – это многогранник, одна из граней которого – произвольный n – угольник A1A2…An, а остальные
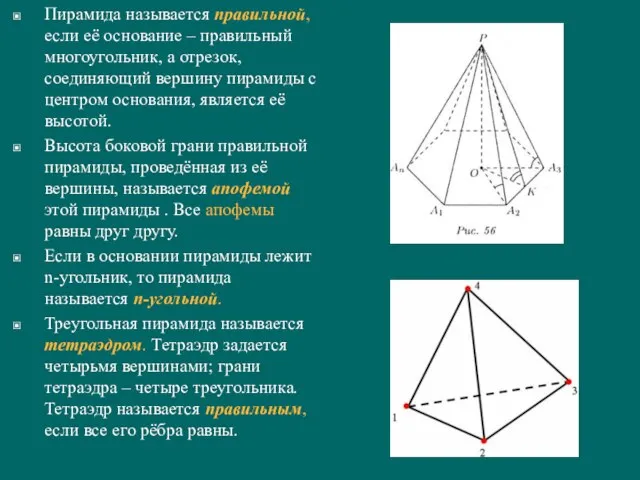
- 13. Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром
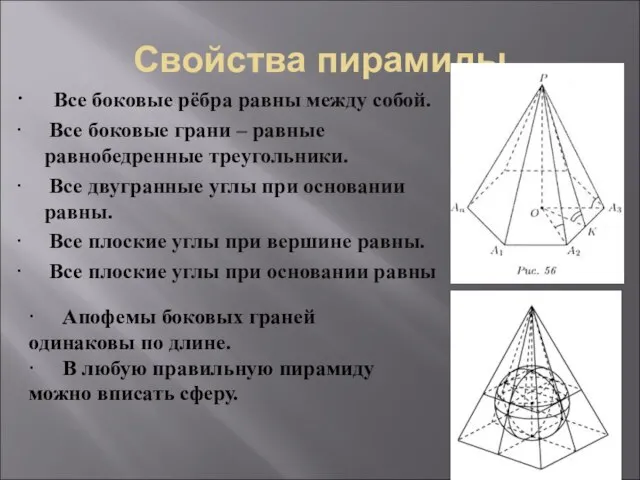
- 14. Свойства пирамиды · Все боковые рёбра равны между собой. · Все боковые грани – равные равнобедренные
- 15. Площадь пирамиды Площадью полной поверхности пирамиды называется сумма площадей всех её граней. Sполн=Sбок+Sосн Площадь боковой поверхности
- 16. Обьём пирамиды Объём пирамиды V=(1/3)*Sосн*h, где S – площадь основания, h – высота пирамиды.
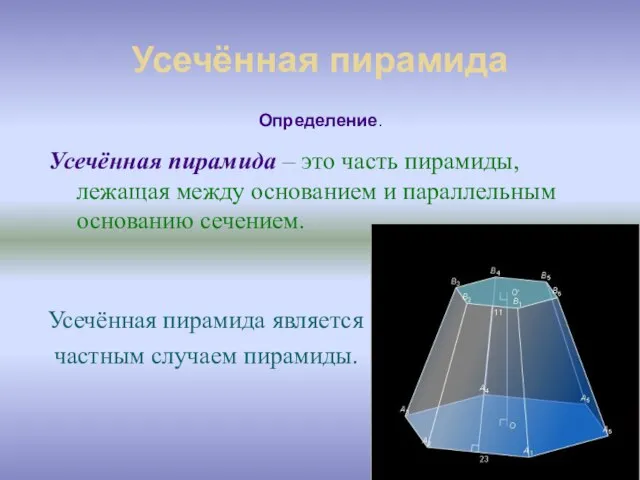
- 17. Усечённая пирамида Усечённая пирамида – это часть пирамиды, лежащая между основанием и параллельным основанию сечением. Усечённая
- 18. Основания усечённой пирамиды – основание исходной пирамиды и многоугольник, полученный при пересечении её плоскостью (A1A2…An и
- 19. Свойства усечённой пирамиды. 1. Боковые рёбра и высота пирамиды делятся секущей плоскостью на пропорциональные отрезки. 2.
- 20. Площадь поверхности правильной усечённой пирамиды: S=(1/2)*m*(P+P1), где m – апофема, P- периметр оснований, P1- периметр боковой
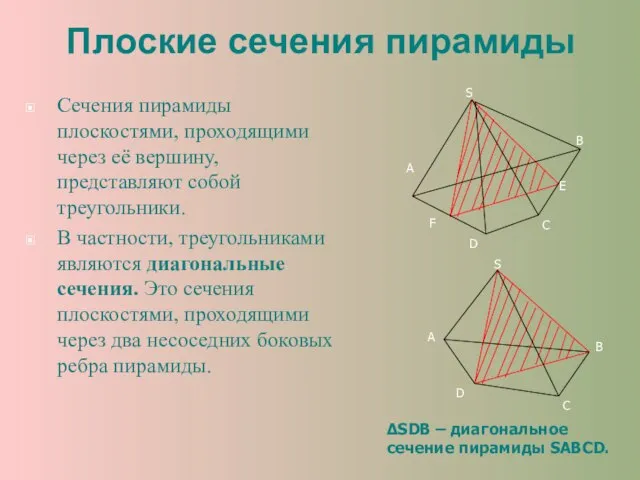
- 21. Плоские сечения пирамиды Сечения пирамиды плоскостями, проходящими через её вершину, представляют собой треугольники. В частности, треугольниками
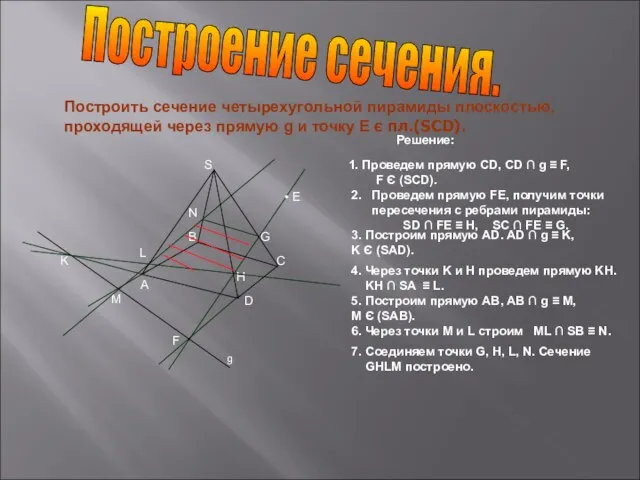
- 22. Построить сечение четырехугольной пирамиды плоскостью, проходящей через прямую g и точку Е є пл.(SCD). 1. Проведем
- 23. Построить сечение четырехугольной пирамиды плоскостью, проходящей через прямую g и точку Е є пл.(SCD). 1. Проведем
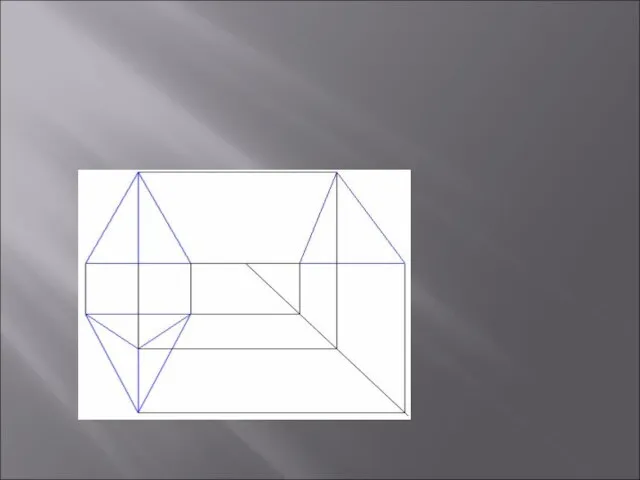
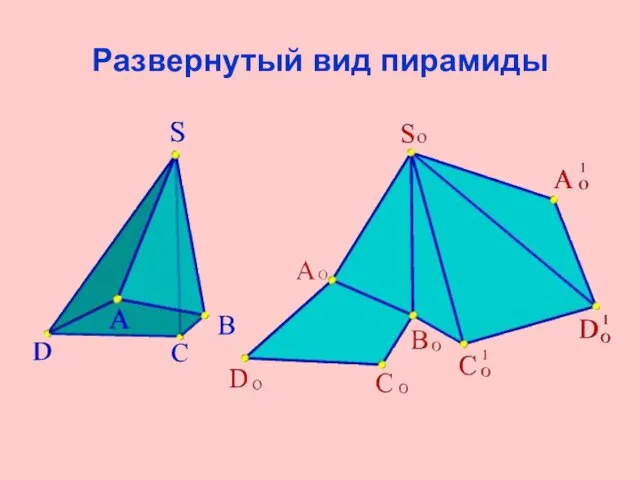
- 24. Развернутый вид пирамиды
- 26. Скачать презентацию















 Нормативно- правовая база по организациипредшкольного образования
Нормативно- правовая база по организациипредшкольного образования Макет
Макет Стоматологическая клиника Стомато-Дент. Шаблон
Стоматологическая клиника Стомато-Дент. Шаблон История развития психопатологии
История развития психопатологии Создание торговой марки Принц Пирогов
Создание торговой марки Принц Пирогов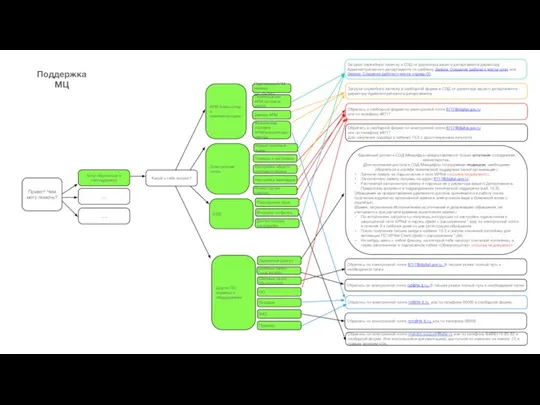 для бота2_2 (3)
для бота2_2 (3) Презентация на тему Система оценивания в соответствии с ФГОС
Презентация на тему Система оценивания в соответствии с ФГОС Теория построения инфокоммуникационных систем и сетей
Теория построения инфокоммуникационных систем и сетей Органы местного самоуправления. Схемы управления муниципальным образованием
Органы местного самоуправления. Схемы управления муниципальным образованием Презентация на тему Доказательства эволюции животных Урок 7 класс
Презентация на тему Доказательства эволюции животных Урок 7 класс Архитектура современных информационных систем. Введение
Архитектура современных информационных систем. Введение Первыми изобретателями прыгучих ходуль считаются калифорнийские акробаты Билл Гаффни и Том Уивер, которые использовали их в свои
Первыми изобретателями прыгучих ходуль считаются калифорнийские акробаты Билл Гаффни и Том Уивер, которые использовали их в свои ТРАДИЦИОННАЯ ПРОГРАММА (под ред. А.Плешакова) «ШКОЛА РОССИИ»
ТРАДИЦИОННАЯ ПРОГРАММА (под ред. А.Плешакова) «ШКОЛА РОССИИ» Системно-деятельностный подход
Системно-деятельностный подход Французская компания Clavel является одним из мировых лидеров по производству декоративных покрытий. Свой путь на российском рынке к
Французская компания Clavel является одним из мировых лидеров по производству декоративных покрытий. Свой путь на российском рынке к Черное и белое духовенство
Черное и белое духовенство Соедините части предложения
Соедините части предложения Presentation_4
Presentation_4 Sweet Box. Про компанію
Sweet Box. Про компанію «Как потратить»
«Как потратить» Причины влияющие на климат
Причины влияющие на климат Международные стандарты финансовой отчетности
Международные стандарты финансовой отчетности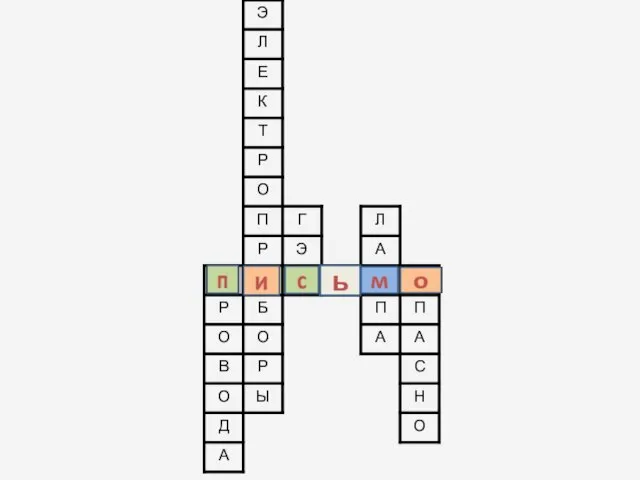 ь
ь Комунальний заклад Гуманітарна гімназія №1 ім. М.І. Пирогова Вінницької міської ради. Кабінет економіки
Комунальний заклад Гуманітарна гімназія №1 ім. М.І. Пирогова Вінницької міської ради. Кабінет економіки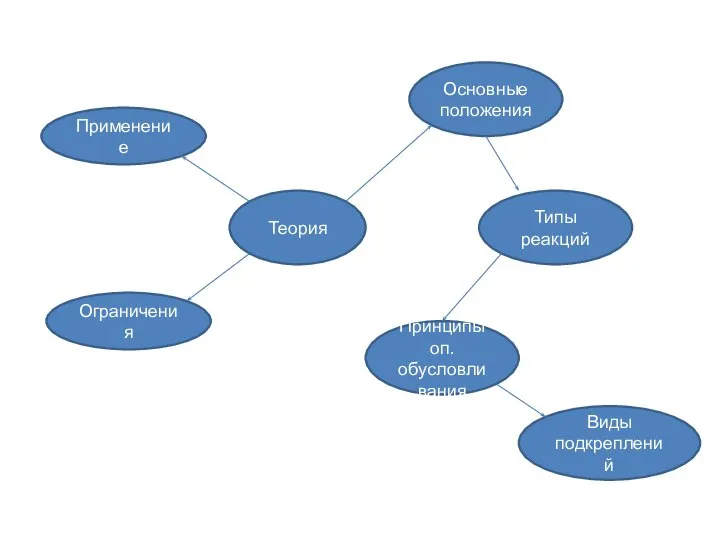 Оперантное обусловливание Б.Ф. Скиннера
Оперантное обусловливание Б.Ф. Скиннера Королева С.В
Королева С.В Шары-гиганты Airbeauty balloons
Шары-гиганты Airbeauty balloons