Содержание
- 2. Содержание: 1) Давайте вспомним. 2)Подобные фигуры 3)Определение подобных треугольников 4)Признаки подобия треугольника 5) Это интересно. 6)
- 3. Давайте вспомним Треугольник- это геометрическая фигура состоящая из трех точек не лежащие на прямой и трех
- 4. Подобные фигуры Чем похожи фигуры? ФОРМОЙ!
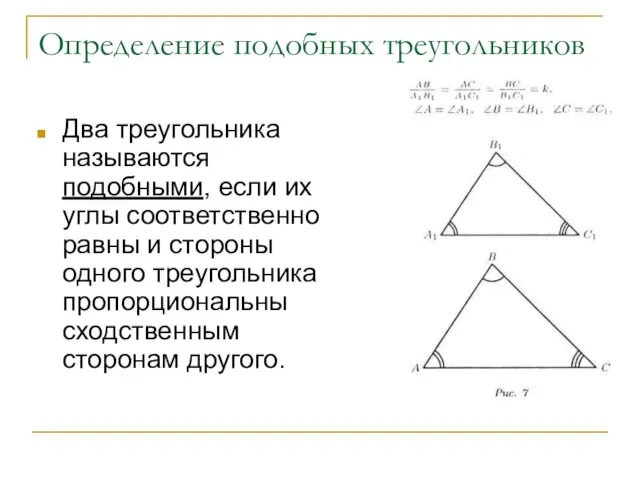
- 5. Определение подобных треугольников Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника
- 6. Признаки подобия треугольников 1 Если два угла одного треугольника соответственно равны двум углам другого, то такие
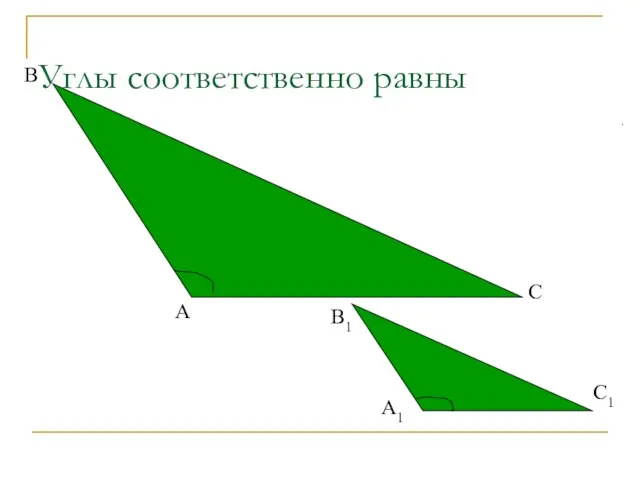
- 7. Углы соответственно равны А В С В1 А1 С1
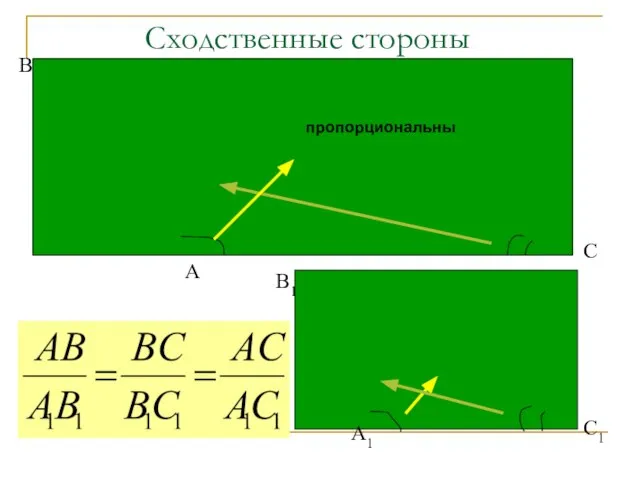
- 8. Сходственные стороны В А С В1 А1 С1 пропорциональны
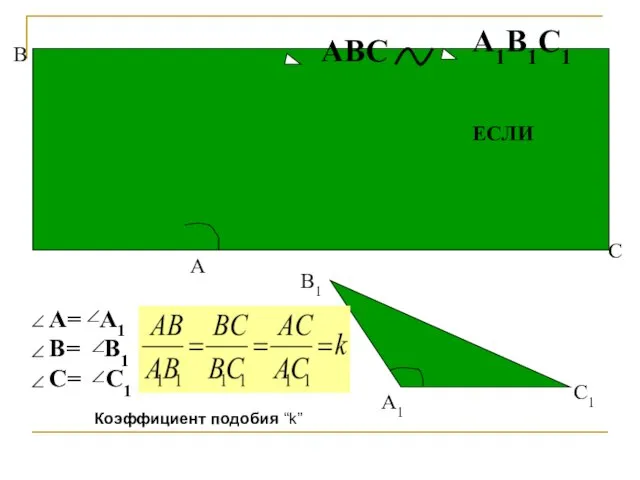
- 9. АВС А1В1С1 ЕСЛИ А= А1 В= В1 С= С1 А В С А1 В1 С1 Коэффициент
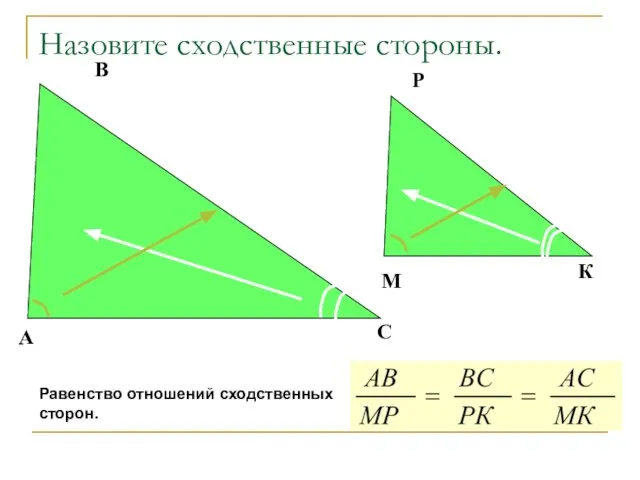
- 10. Назовите сходственные стороны. А С В М К Р Равенство отношений сходственных сторон.
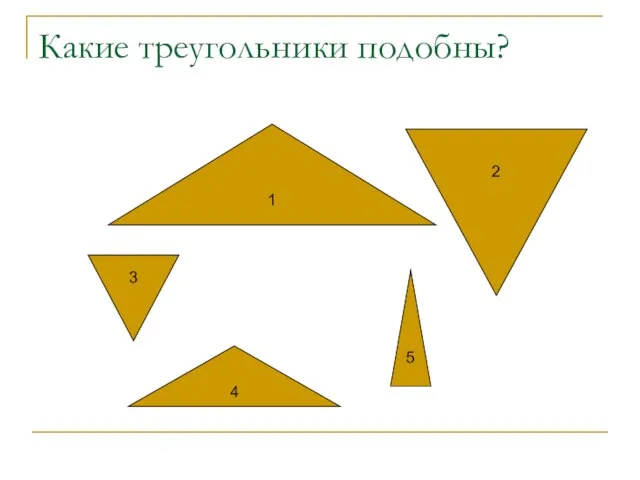
- 11. Какие треугольники подобны? 1 4 2 3 5
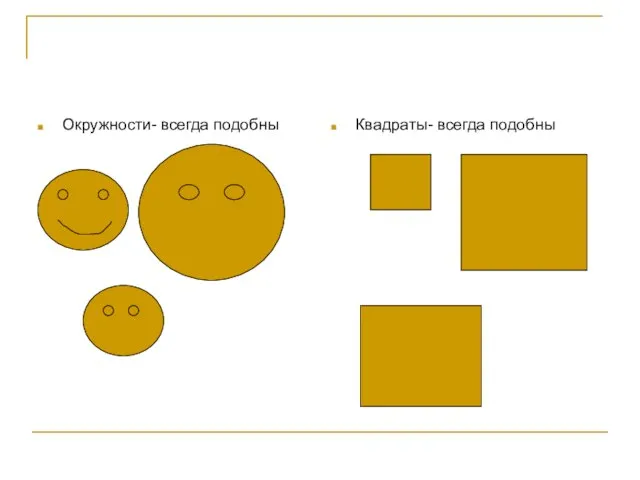
- 12. Окружности- всегда подобны Квадраты- всегда подобны
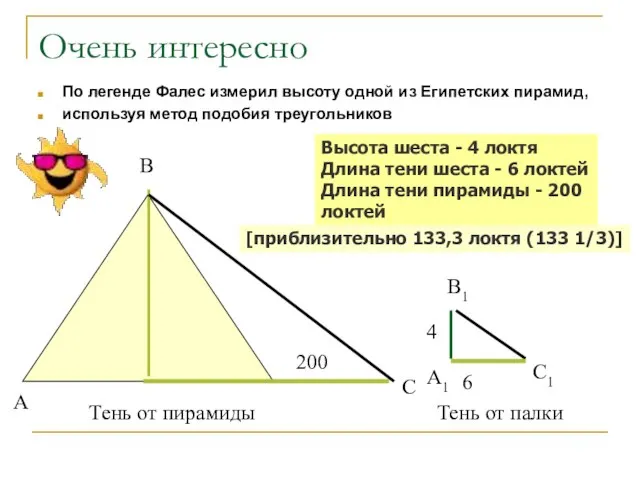
- 13. Очень интересно По легенде Фалес измерил высоту одной из Египетских пирамид, используя метод подобия треугольников 200
- 14. Еще немного о треугольниках.
- 15. Пропорциональные отрезки в треугольнике Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам
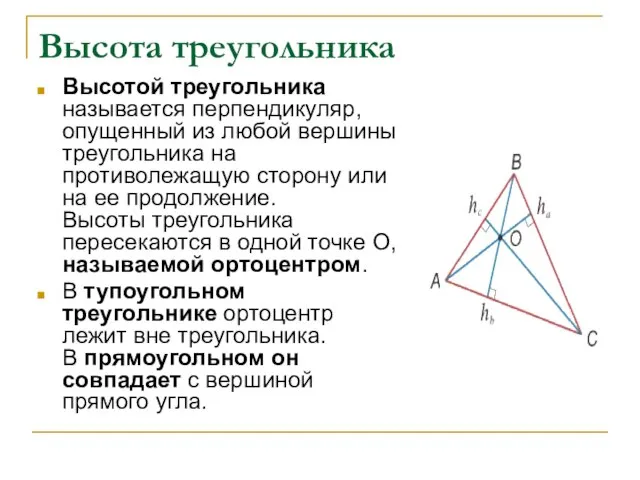
- 16. Высота треугольника Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на
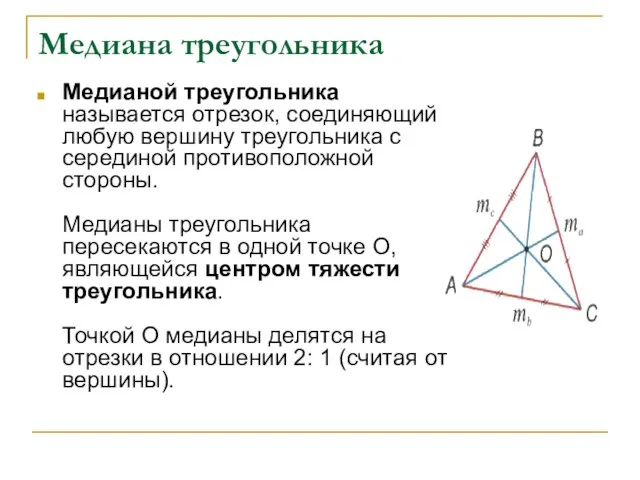
- 17. Медиана треугольника Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Медианы треугольника
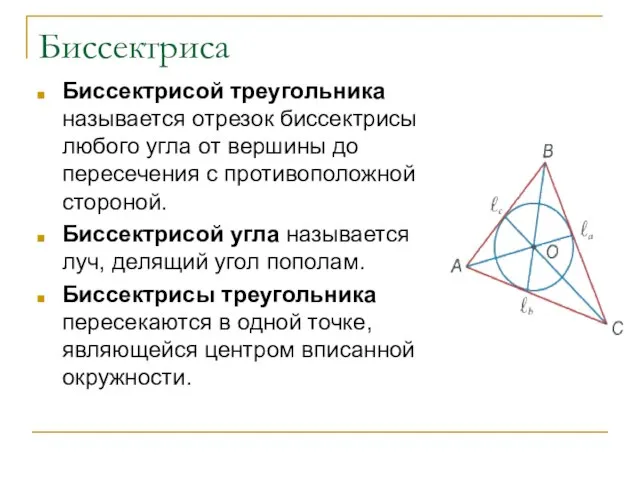
- 18. Биссектриса Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной. Биссектрисой
- 20. Скачать презентацию





 Научно-исследовательская работа «Влияние наращивания на структуру и здоровье ногтей»
Научно-исследовательская работа «Влияние наращивания на структуру и здоровье ногтей»  Цифровые носители информации
Цифровые носители информации Остаться в живых
Остаться в живых Презентация на тему горы Южной Сибири
Презентация на тему горы Южной Сибири 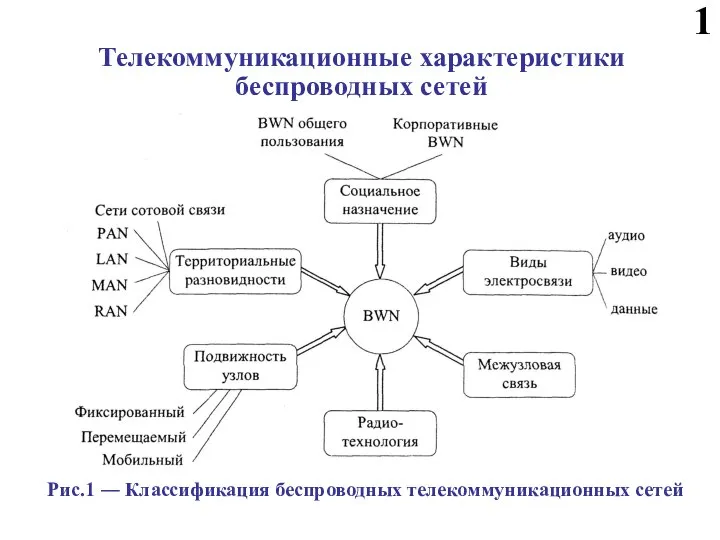 Идеология управления сетью в UMTS. Телекоммуникационные характеристики беспроводных сетей (часть 1)
Идеология управления сетью в UMTS. Телекоммуникационные характеристики беспроводных сетей (часть 1) Быт Японии
Быт Японии Испанская барочная живопись
Испанская барочная живопись Этот удивительный мир
Этот удивительный мир Презентация на тему Князья Киевской Руси
Презентация на тему Князья Киевской Руси  Православный храм
Православный храм Утилизация попутного нефтяного газа при освоении месторождений ООО «Нарьянмарнефтегаз». Проблемы и пути их решения.
Утилизация попутного нефтяного газа при освоении месторождений ООО «Нарьянмарнефтегаз». Проблемы и пути их решения. Презентация на тему Механизм разработки и установления вывозных таможенных пошлин
Презентация на тему Механизм разработки и установления вывозных таможенных пошлин  Региональная академия делового образования
Региональная академия делового образования Развлекательная программа на январь в рамках города Воронежа
Развлекательная программа на январь в рамках города Воронежа НИИ Спецвузавтоматика (Минобрнауки России)
НИИ Спецвузавтоматика (Минобрнауки России) Познай свой характер
Познай свой характер Гончарный промысел
Гончарный промысел «Дети и война»
«Дети и война» Презентация на тему Объект и диагностический инструментарий мониторинга результативности освоения детьми ООП дошкольного образ
Презентация на тему Объект и диагностический инструментарий мониторинга результативности освоения детьми ООП дошкольного образ МОУ Рождественская ООШ Карасукского района НСО Баязитов Алексей Андреевич Преподавание математики в классе с различным уровнем п
МОУ Рождественская ООШ Карасукского района НСО Баязитов Алексей Андреевич Преподавание математики в классе с различным уровнем п Басня
Басня Извлеченные уроки
Извлеченные уроки Советск – экологическая бомба? Насколько безопасно жить в городе Советске?
Советск – экологическая бомба? Насколько безопасно жить в городе Советске? Фалес
Фалес Презентация на тему Разнообразие и распространение организмов на Земле
Презентация на тему Разнообразие и распространение организмов на Земле Презентация на тему Н и НН в страдательных причастиях прошедшего времени
Презентация на тему Н и НН в страдательных причастиях прошедшего времени Метод круговой тренировки для повышения функциональных способностей боксеров
Метод круговой тренировки для повышения функциональных способностей боксеров Государственная (итоговая) аттестация выпускников 9 классов по алгебре и русскому языку в новой форме.
Государственная (итоговая) аттестация выпускников 9 классов по алгебре и русскому языку в новой форме.