ГЕОМЕТРИЯ

ТЕМА:
ТРАПЕЦИЯ

Выполнил: ученик 10 “Б” класса
Средней школы № 1143
Галкин Владимир

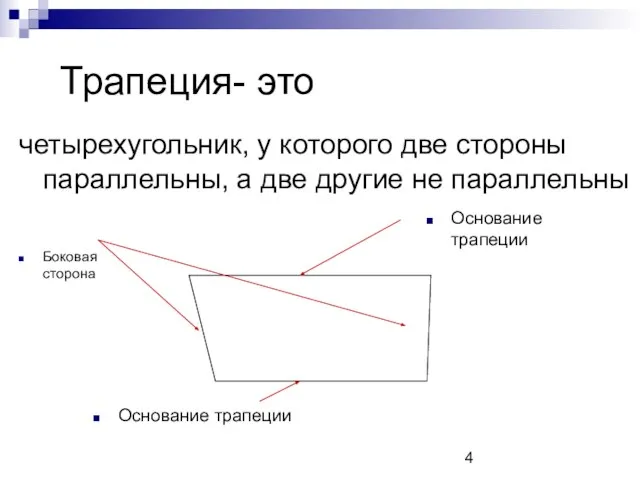
Трапеция- это
четырехугольник, у которого две стороны параллельны, а две другие не параллельны
Основание трапеции
Основание трапеции
Боковая сторона

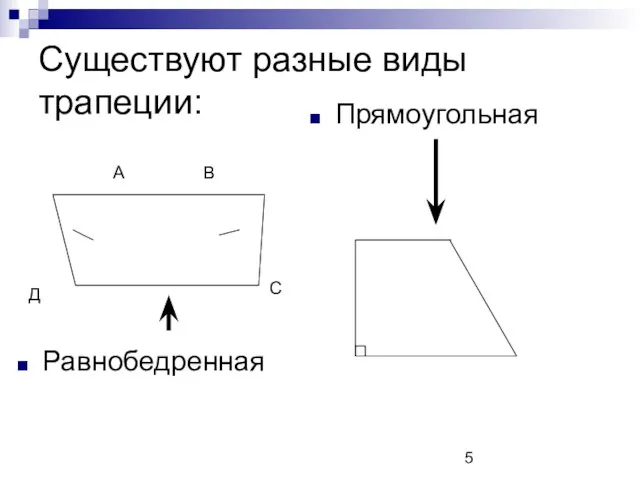
Существуют разные виды трапеции:
Равнобедренная
Прямоугольная
А
В
С
Д

Задачи
Часть А:

Задача 1:Найдите углы B и D трапеции ABCD с основаниями AD и ВС, если А=36, С=117.
Дано:ABCD-трапеция ; А=36; C=117
Найти: В, D
Решение:
А+ В=180, значит В=144.
С+ В=180, значит D=63.
D
А
В
С

Задача 2:Один из углов равнобедренной трапеции равен 68.Найдите остальные углы трапеции.
Дано: трапеция, 1=68.
Найти: 2, 3, 4.
Решение:
1= 2 (углы при основании равны)
3=180- 1=112.
4= 3=112.
2=68.
1
2
3
4

Задача 3: Основания прямоугольной трапеции равны 4 и 7, один из углов равен 60.Найти большую боковую сторону трапеции.
Дано:ABCD-трапеция. D=60.
BC=4,AD=7.
Найти: CD-?
Решение:
Проведем высоту СН.
Тогда HD=AD-BC=3.
Применим теорему синусов
HD = CH Отсюда CH= 3 корня из 3
Sin 30 sin 60
CD2=9+27=36 (Теорема Пифагора)
CD=6.
А
D
B
C
Н

Задача 4: Найти площадь прямоугольной трапеции, у которой две меньшие стороны равны 6, а больший угол равен 135о.
Дано:ABCD-трапеция, А=90;AB=BC=6;
BCD=1350
Найти: S-?
Решение:
HCD=135-90=45; CDH=45.
DH = CH Отсюда DH=6
sin45 sin 45
S=0,5 ( BC+AD) CH=0,5(5+12)6=54
А
D
B
C
Н

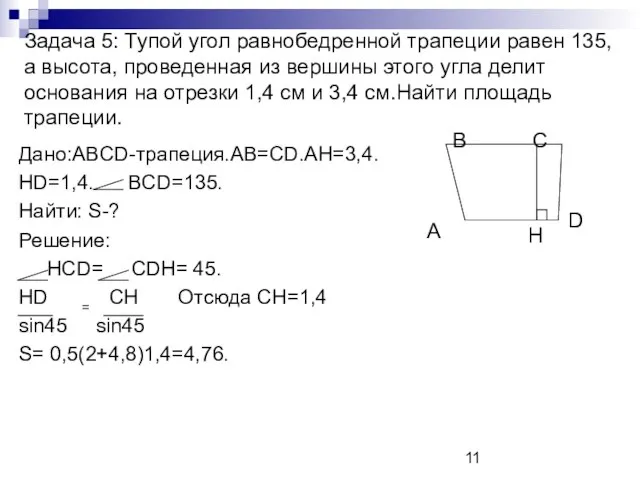
Задача 5: Тупой угол равнобедренной трапеции равен 135, а высота, проведенная из вершины этого угла делит основания на отрезки 1,4 см и 3,4 см.Найти площадь трапеции.
Дано:ABCD-трапеция.AB=CD.AH=3,4.
HD=1,4. BCD=135.
Найти: S-?
Решение:
HCD= CDH= 45.
HD = CH Отсюда СН=1,4
sin45 sin45
S= 0,5(2+4,8)1,4=4,76.
D
А
В
С
H

Задача 6: Основания трапеции относятся как 2:3, а средняя линия равна 5. Найти основания.
Дано: трапеция АDCD.MN=5.
BC:AD=2:3.
Найти: AD;CD.
Решение:
Пусть х- коефиециент пропорциональности. Тогда ВС=2х,AD=3x. MN=0,5(AD+BC)
2,5x=5
X=2.
Значит АD=6, a BC=4.
D
А
В
С
М
N

Задача 7: Дана равнобокая трапеция. Средняя линия равна боковой стороне. Основания равны 8 и 16. Найти площадь трапеции.
Дано: АBCD- трапеция.AB=CD;MN=AB;
BC=8;AD=16.
Найти: S
Решение: MN=0,5(BC+AD)=12.Значит AB=12.AH=4
BH2=AB2-AH2;
BH2= 144-16
BH=8 корней из 2ж
S=MN BH=96 корней из 2
D
А
В
С
М
N

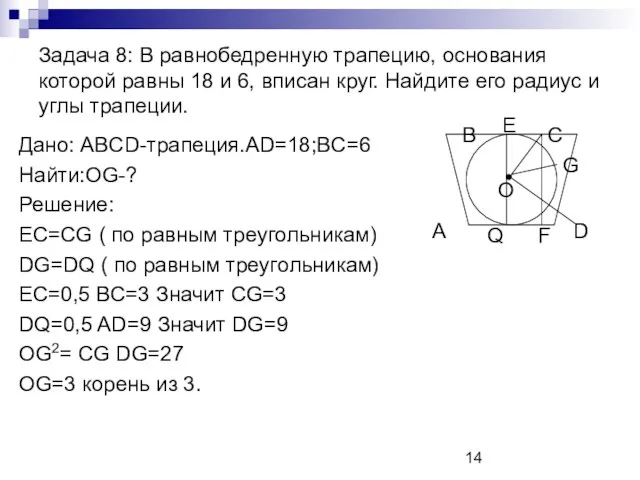
Задача 8: В равнобедренную трапецию, основания которой равны 18 и 6, вписан круг. Найдите его радиус и углы трапеции.
Дано: ABCD-трапеция.AD=18;BC=6
Найти:ОG-?
Решение:
EC=CG ( по равным треугольникам)
DG=DQ ( по равным треугольникам)
EC=0,5 BC=3 Значит СG=3
DQ=0,5 AD=9 Значит DG=9
OG2= CG DG=27
OG=3 корень из 3.
А
В
С
D
E
F
G
О
Q

Часть Б

Задача 1: Площадь равнобокой трапеции равна S, угол между ее диагоналями, противолежащий боковой стороне, равен а. Найти высоту трапеции.
Дано:ABCD- трапеция; S- её площадь
а .ВС и AD основания.
Найти:CK-?
Решение:
Пусть О – точка пересечения диагоналей данной трапеции ABCD, AB=CD, AOB=a.
Т.к АОВ- внешний угол AOD, AO=OD,то CAD= a2 .
Пусть СК=Н- высота трапеции
Из АКС ( АКС=90); АК=Н ctg 2a
Тогда площадь трапеции S = 0,5(AD+BC)CK=AK CK= H2 ctg 2a
H=корень из S tg 2a
D
А
В
С
K
a
О

Задача 2: Большее основание вписанной в круг трапеции равно диаметру круга, а угол при основании равен а. В каком отношении точка пересечения диагоналей трапеции делит её высоту?
Дано: ABCD- трапеция.
Найти:
Решение:
Пусть основание AD равнобокой трапеции ABCD есть диаметр круга, описанного около трапеции, тогда центр О круга – середина AD.
Высота КО трапеции проходит через точку L пересечения диагоналей, BLC подобен ALD,
KL:LO=LC:LD.
D
А
В
С
о
К
L

ACD- вписанный, опирающийся на диаметр , поэтому
ACD=90. ACD и AOL- прямоугольные с общим острым углом при вершине А.Отсюда, ALO= ADC=a.
Тогда KLC= OLD=a, CLD=180-2a,из DLCD
( LCD=90);
LC:LD=cos CLD=cos (180-2a)=-cos2a.

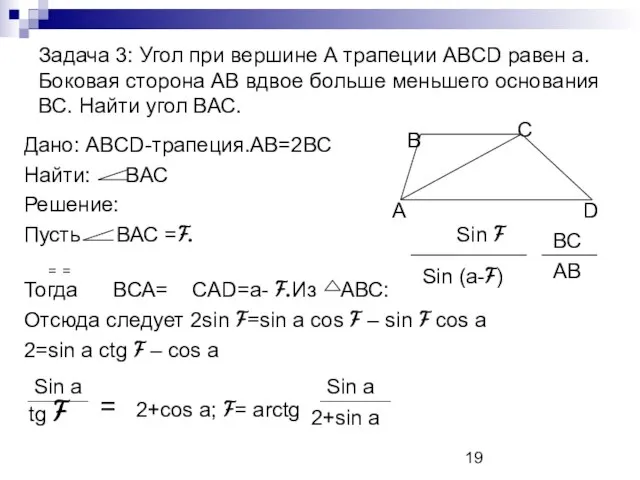
Задача 3: Угол при вершине А трапеции ABCD равен а.
Боковая сторона АВ вдвое больше меньшего основания ВС. Найти угол ВАС.
Дано: ABCD-трапеция.АВ=2ВС
Найти: ВАС
Решение:
Пусть ВАС =F. Sin F = =
Тогда ВСА= СAD=a- F.Из АВС:
Отсюда следует 2sin F=sin a cos F – sin F cos a
2=sin a ctg F – cos a
2+cos a; F= arctg
А
В
С
D
Sin (a-F)
ВС
АВ
Sin a
tg F
=
Sin a
2+sin a

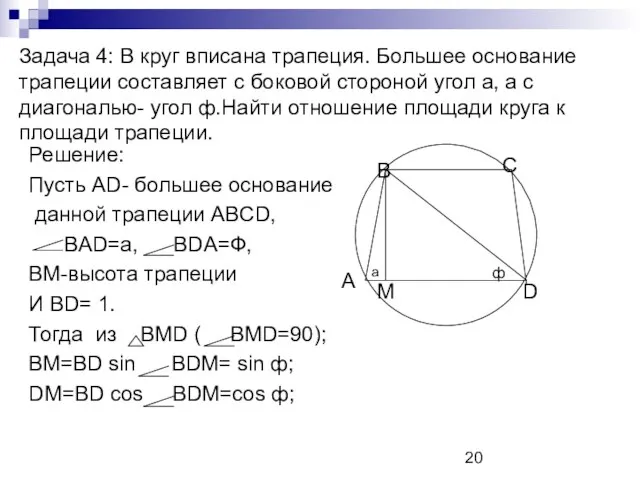
Задача 4: В круг вписана трапеция. Большее основание трапеции составляет с боковой стороной угол а, а с диагональю- угол ф.Найти отношение площади круга к площади трапеции.
Решение:
Пусть АD- большее основание
данной трапеции ABCD,
BAD=a, BDA=Ф,
BM-высота трапеции
И BD= 1.
Тогда из BMD ( BMD=90);
BM=BD sin BDM= sin ф;
DM=BD cos BDM=cos ф;
А
В
С
D
M
a
ф

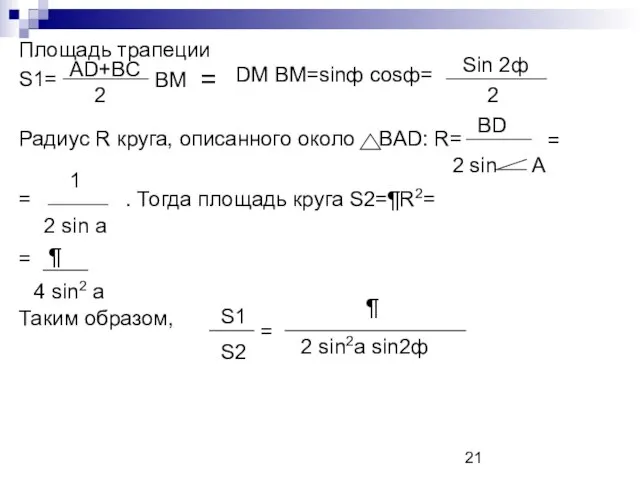
Площадь трапеции
S1=
Радиус R круга, описанного около BAD: R=
= . Тогда площадь круга S2=¶R2=
=
Таким образом,
AD+BC
2
=
BM
DM BM=sinф cosф=
Sin 2ф
2
BD
2 sin A
=
1
2 sin a
¶
4 sin2 a
S1
S2
=
¶
2 sin2a sin2ф

ЧАСТЬ С

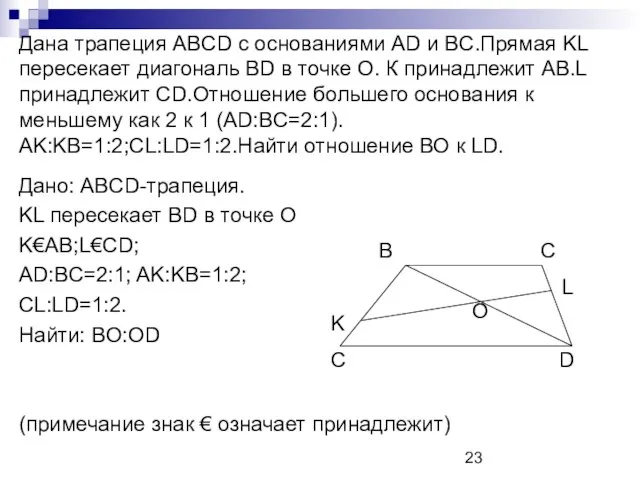
Дана трапеция ABCD с основаниями AD и BC.Прямая KL пересекает диагональ BD в точке О. К принадлежит AB.L принадлежит CD.Отношение большего основания к меньшему как 2 к 1 (AD:BC=2:1).
AK:KB=1:2;CL:LD=1:2.Найти отношение ВО к LD.
Дано: ABCD-трапеция.
KL пересекает BD в точке О
K€AB;L€CD;
AD:BC=2:1; AK:KB=1:2;
CL:LD=1:2.
Найти: BO:OD
(примечание знак € означает принадлежит)
B C
L
K
C D
O

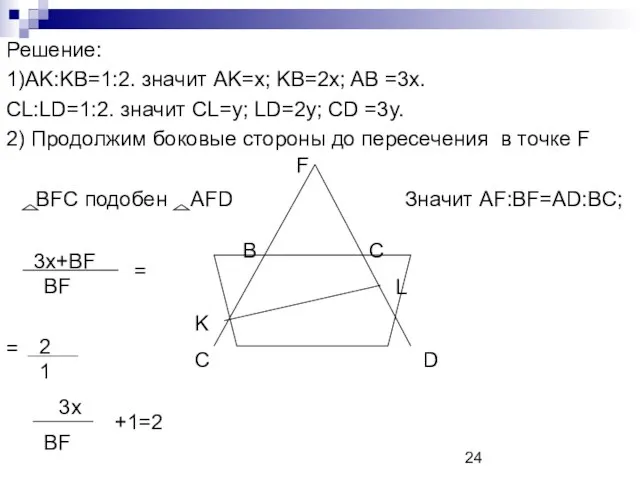
Решение:
1)AK:KB=1:2. значит АK=x; KB=2x; AB =3x.
CL:LD=1:2. значит СL=y; LD=2y; CD =3y.
2) Продолжим боковые стороны до пересечения в точке F
BFC подобен AFD Значит AF:BF=AD:BC;
=
B C
L
K
C D
F
3x+BF
BF
=
2
1
3x
BF
+1=2

BF=3x
AF=6x
Аналогично
FC=3y; FD=6y.
3)По теореме Менелая BFD и секущая KL
BO:OD=4:5.
FL DO BK
LD BO KF
=1
4y DO 2x
2y BO 5x
=1
DO
BO
=
5
4

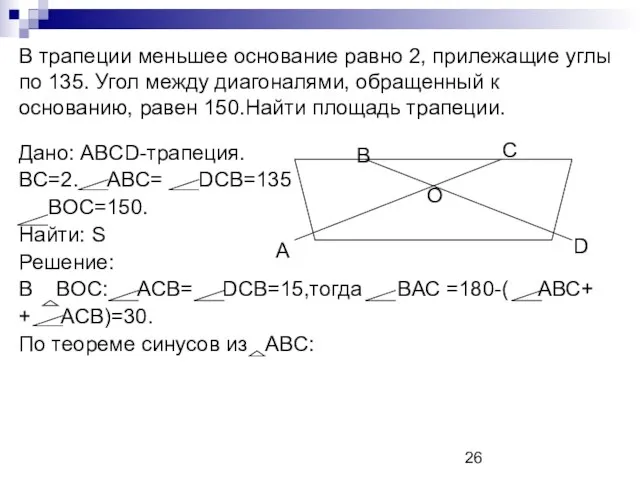
В трапеции меньшее основание равно 2, прилежащие углы по 135. Угол между диагоналями, обращенный к основанию, равен 150.Найти площадь трапеции.
Дано: ABCD-трапеция.
BC=2. ABC= DCB=135
BOC=150.
Найти: S
Решение:
В BOC: ACB= DCB=15,тогда ВАС =180-( АВС+
+ АСВ)=30.
По теореме синусов из АВС:
А
В
С
D
O

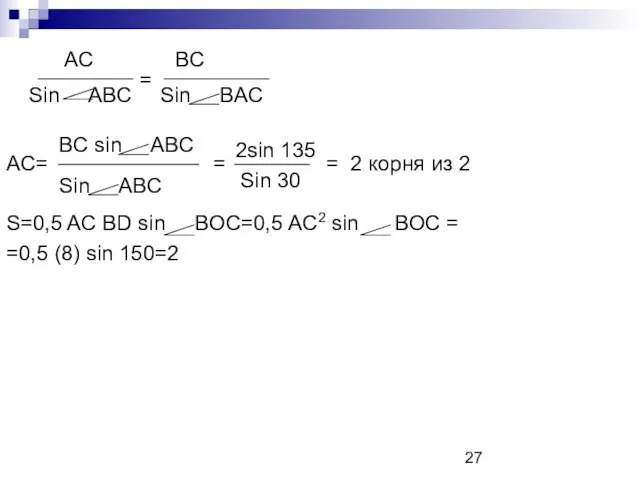
AC= = = 2 корня из 2
S=0,5 AC BD sin BOC=0,5 AC2 sin BOC =
=0,5 (8) sin 150=2
2sin 135
AC
Sin ABC
=
BC
Sin BAC
BC sin ABC
Sin ABC
Sin 30

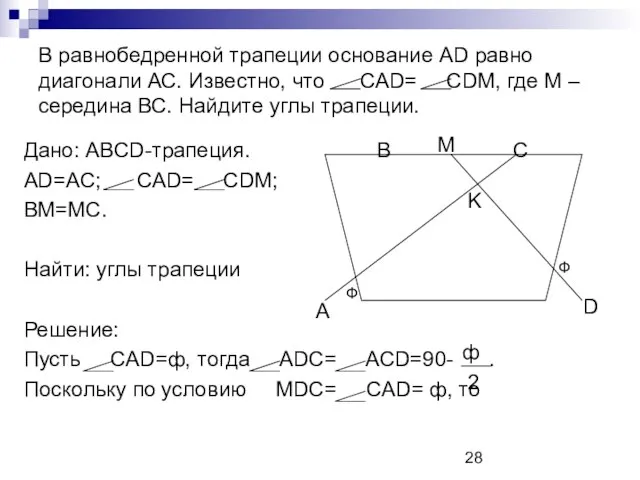
В равнобедренной трапеции основание AD равно диагонали АС. Известно, что САD= СDM, где М –
середина ВС. Найдите углы трапеции.
Дано: ABCD-трапеция.
AD=AC; CAD= CDM;
BM=MC.
Найти: углы трапеции
Решение:
Пусть СAD=ф, тогда ADC= ACD=90- .
Поскольку по условию MDC= CAD= ф, то
A
B
C
D
M
K
Ф
Ф
ф
2

CMD= MDA= ADC- MDC=90- ф,
МDC=90+
По теореме синусов для треугольника MDC надем
,
MD=CD
Но М- середина ВС. Следовательно, проекция МD на AD равна 0,5AD, т.е
AD=2MD cos(90 - )=2CD
3
2
ф
2
MD CD
Sin ( 90+ )
ф
2
=
Sin ( 90- )
3
2
ф
cos
2
ф
cos
3
2
ф
2
3
ф
cos
ф
2
Sin
3
2
ф
cos
2
3
ф

Из равнобедренного треугольника ACD найдем
AD=
Приравнивая два выражения для AD, получим уравнение
Можно доказать,что cos ф = сos (2cos ф - 1) ,
2sin ф sin ==cos ф-cos2ф
CD
2sin
ф
2
2cos
ф
2
sin
3
2
ф
cos
3
2
ф
=
1
2sin
2
ф
3
2
ф
2
3
2
ф
2

Сократив теперь в числителе и знаменателе левой части уравнения ,освободившись от знаменателя, придем к уравнению 2 cos 2ф=1, т.е 2ф=60, ф=30.
Таким образом, два угла трапеции равны 75, два оставшихся 105.
cos
ф
2