Графический подход к решению задач при подготовке к ЕГЭ

Устная работа
Задания типа В8

Ответить на вопросы:
В каких заданиях ЕГЭ по математике используются графики функций?
Что такое область определения функции, область значений функции?
Как определить по графику производной функции промежутки возрастания и убывания?
Чему равно значение производной функции в точках экстремума?

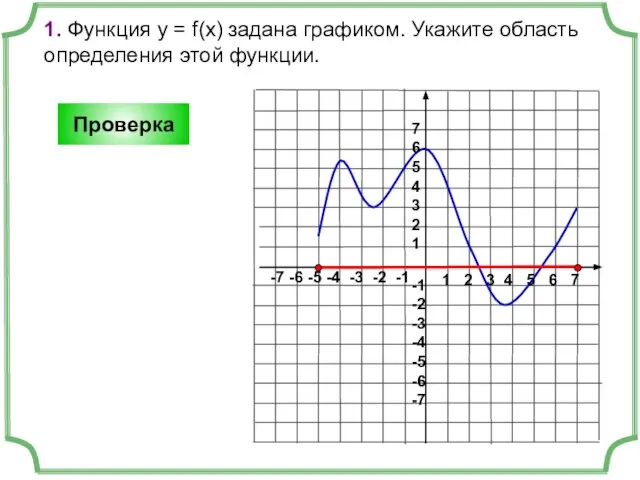
1. Функция у = f(x) задана графиком. Укажите область определения этой функции.
Проверка
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7

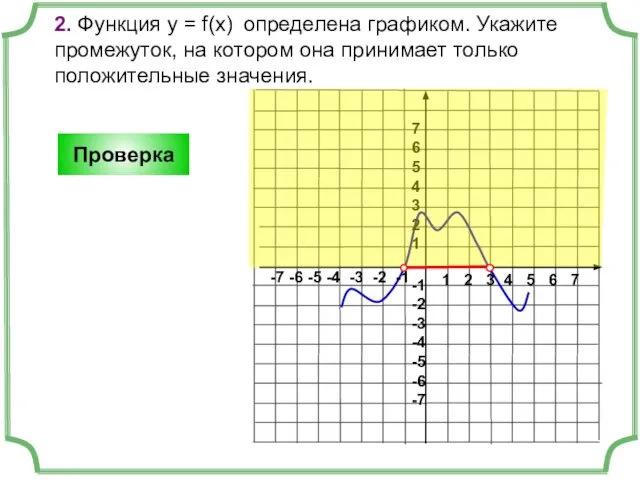
2. Функция у = f(x) определена графиком. Укажите промежуток, на котором она принимает только положительные значения.
Проверка
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7

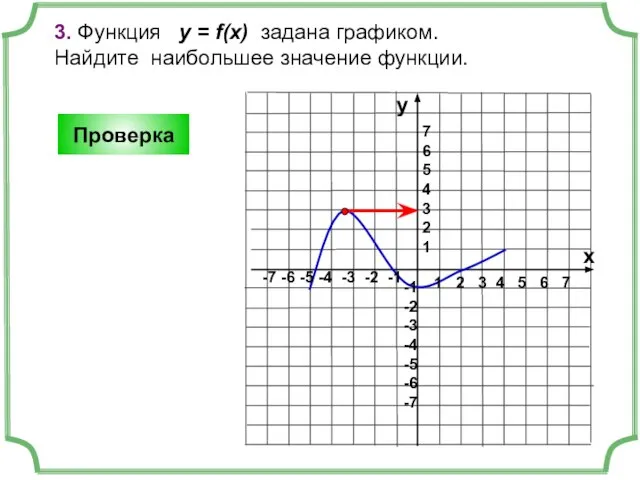
3. Функция у = f(x) задана графиком.
Найдите наибольшее значение функции.
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
у
х
Проверка

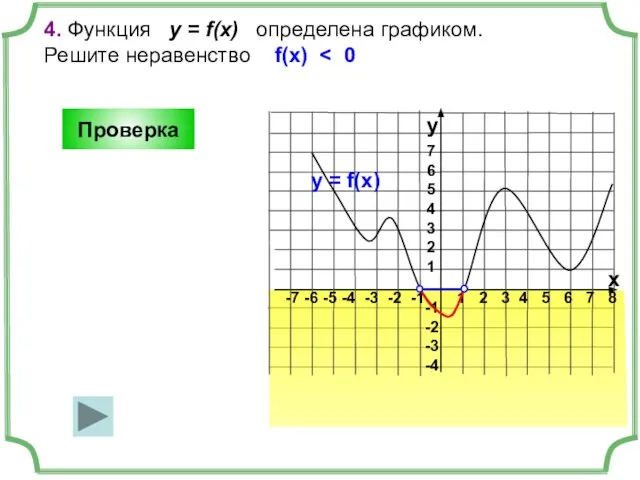
1 2 3 4 5 6 7 8
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
4. Функция у = f(x) определена графиком.
Решите неравенство f(x) < 0
y
x
у = f(x)
Проверка

Работа в тетрадях
Задания типа В8

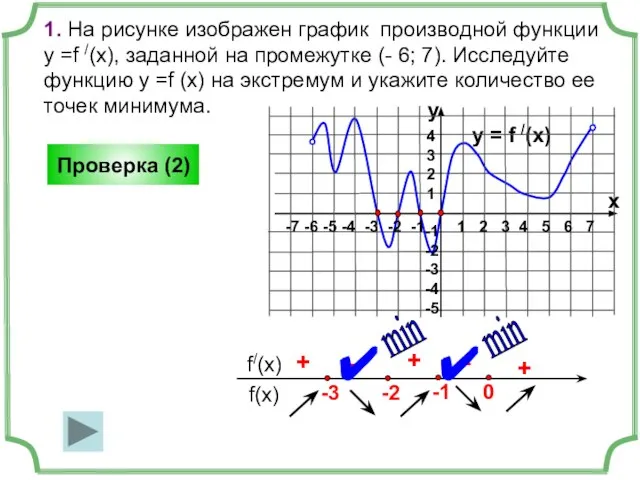
1. На рисунке изображен график производной функции
у =f /(x), заданной на промежутке (- 6; 7). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
Проверка (2)
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x

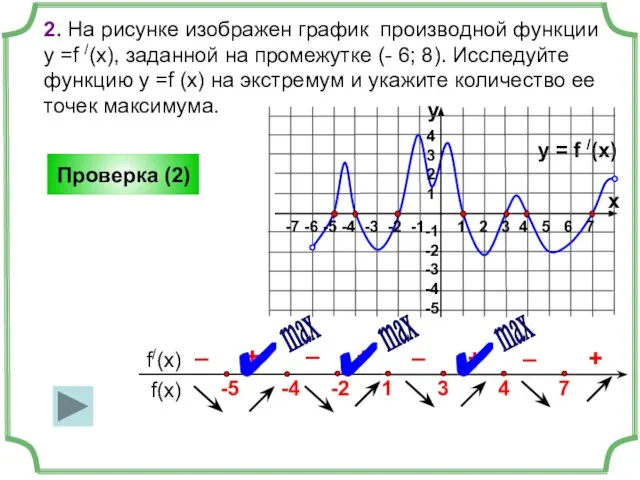
2. На рисунке изображен график производной функции
у =f /(x), заданной на промежутке (- 6; 8). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек максимума.
Проверка (2)
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x

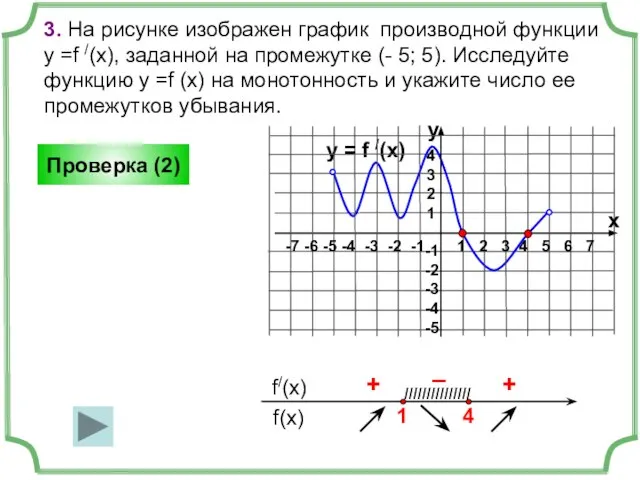
3. На рисунке изображен график производной функции
у =f /(x), заданной на промежутке (- 5; 5). Исследуйте функцию у =f (x) на монотонность и укажите число ее промежутков убывания.
Проверка (2)
+
–
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
IIIIIIIIIIIIIII

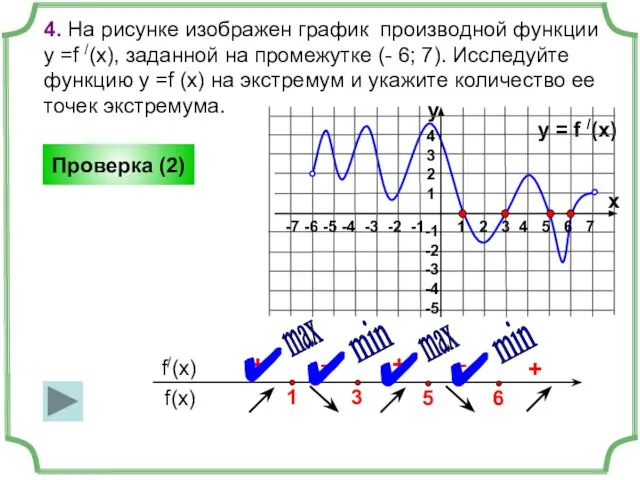
4. На рисунке изображен график производной функции
у =f /(x), заданной на промежутке (- 6; 7). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек экстремума.
Проверка (2)
+
–
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
+

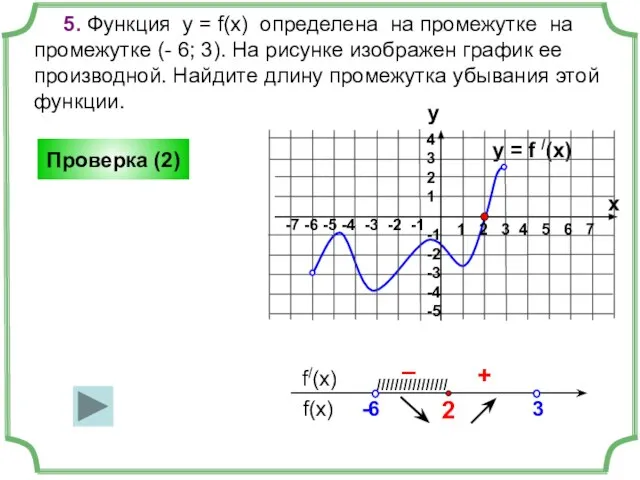
y = f /(x)
5. Функция у = f(x) определена на промежутке на промежутке (- 6; 3). На рисунке изображен график ее производной. Найдите длину промежутка убывания этой функции.
+
–
Проверка (2)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
IIIIIIIIIIIIIIII
y
x

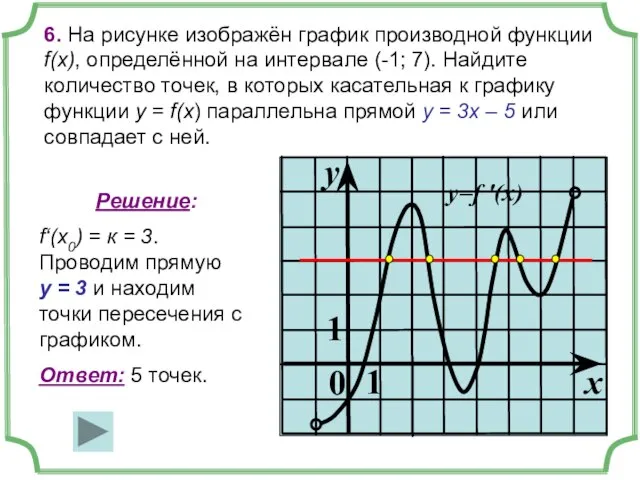
6. На рисунке изображён график производной функции f(x), определённой на интервале (-1; 7). Найдите количество точек, в которых касательная к графику функции y = f(x) параллельна прямой у = 3х – 5 или совпадает с ней.
Решение:
f‘(x0) = к = 3. Проводим прямую у = 3 и находим точки пересечения с графиком.
Ответ: 5 точек.

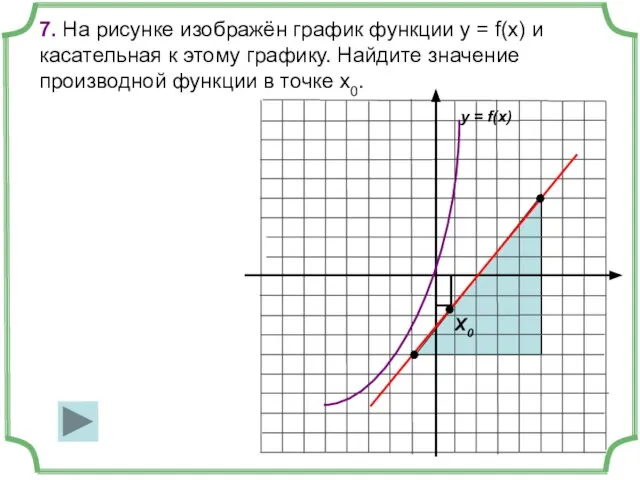
7. На рисунке изображён график функции y = f(x) и касательная к этому графику. Найдите значение производной функции в точке х0.
Х0
y = f(x)

Работа в тетрадях
Задания типа С5

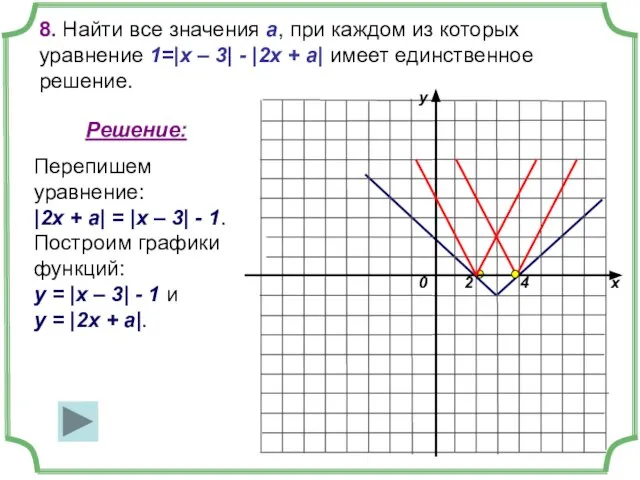
8. Найти все значения а, при каждом из которых уравнение 1=|x – 3| - |2x + a| имеет единственное решение.
Решение:
Перепишем уравнение: |2x + a| = |x – 3| - 1. Построим графики функций: у = |x – 3| - 1 и у = |2x + a|.
2
4
0

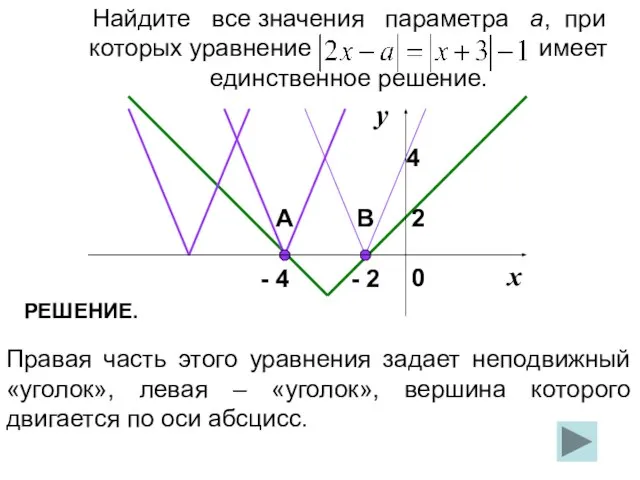
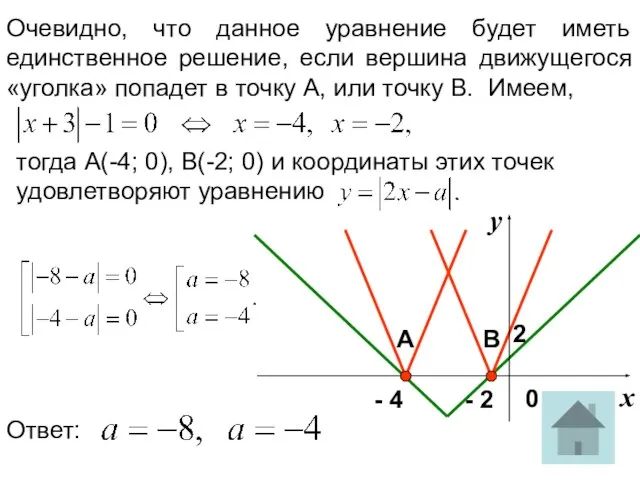
Очевидно, что данное уравнение будет иметь единственное решение, если вершина движущегося «уголка» попадет в точку с координатами (2; 0) или (4; 0). Следовательно, координаты этих точек удовлетворяют уравнению у = |2x + a|. Значит,
0 = |4 + a| или 0 = |8 + a|
а = - 4 а = - 8.
Ответ: - 8 или – 4.
9. Найти все значения а, при каждом из которых уравнение |2x – а| = |x + 3| - 1 имеет единственное решение.

Найдите все значения параметра а, при которых уравнение имеет единственное решение.
Правая часть этого уравнения задает неподвижный «уголок», левая – «уголок», вершина которого двигается по оси абсцисс.
2
А
В
РЕШЕНИЕ.

2
х
у
- 2
- 4
0

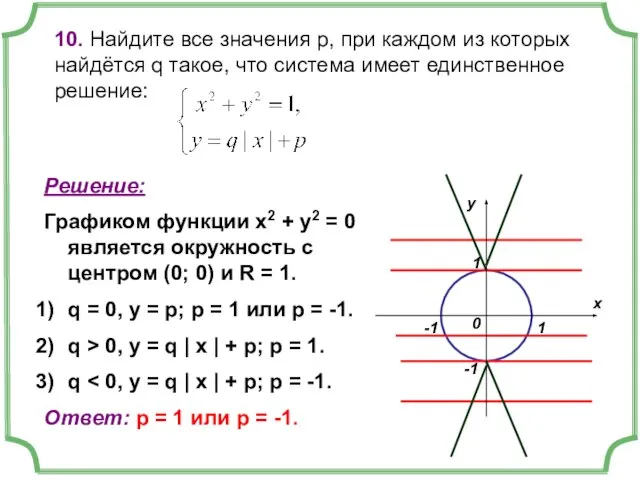
10. Найдите все значения р, при каждом из которых найдётся q такое, что система имеет единственное решение:
Решение:
Графиком функции х2 + у2 = 0 является окружность с центром (0; 0) и R = 1.
q = 0, у = р; р = 1 или р = -1.
q > 0, y = q | x | + p; p = 1.
q < 0, y = q | x | + p; p = -1.
Ответ: р = 1 или р = -1.
0