Гравитационное поле Земли

Гравитационная карта Земли
Гравитационные аномалии нашей планеты: желтые участки - самая высокая сила тяжести, красные высокая сила тяжести, синие и голубые участки - пониженная сила тяжести Картинки продемонстрировали специалисты из Института астрономической физики и физической геодезии Технического университета Мюнхена Точную форму Земли удалось определить с помощью данных, полученных с помощью спутника GОСЕ (Gravity Field and Steady-State Ocean Circulation Explorer) Европейского космического агентства. Он был запущен в марте 2009 года, летает на высоте порядка 250 километров - ниже, чем другие аппараты. И улавливает малейшие гравитационные аномалии.
В Евразии и Африке в основном попадаются участки с повышенным притяжением (обозначены красным и желтым). А вот в Северной Америке сила тяжести меньше (синие участки). Разница в силе тяжести между США и Россией может достигать 0,04 процента.

Наличие всемирного тяготения приводит к представлению о гравитационном поле (как особой формы материи), в пределах которого на каждое тело действует сила, прямо пропорциональная массе этого тела.
Гравитационное поле представляет собой разновидность силового поля: на частицы, помещённые в каждой точке такого поля, действуют силы, прямо пропорциональные определённому физическому свойству этих частиц – массе.
Земля также окружена гравитационным полем (или полем тяготения), в котором на тело действуют силы, пропорциональные их массам.
Гравитационное поле Земли

Яковлева Т.Ю.
В каждой точке поля Земли можно определить отношение силы, действующей на точечное тело, к массе этого тела; это отношение не зависит от вещества тела, и равно ускорению, сообщаемому силой тяготения в данной точке поля:
Гравитационное поле Земли

Яковлева Т.Ю.
Напряженность поля g представляет собой векторную величину, направление которой определяется направлением гравитационной силы F, а численное значение — формулой ускорения свободного падения.
Напряженность гравитационного поля совпадает по величине, направлению и единицам измерения с ускорением свободного падения, хотя по своему физическому смыслу, это совершенно разные физические величины. В то время, как напряженность поля характеризует состояние пространства в данной точке, сила и ускорение появляются только тогда, когда в данной точке находится пробное тело.

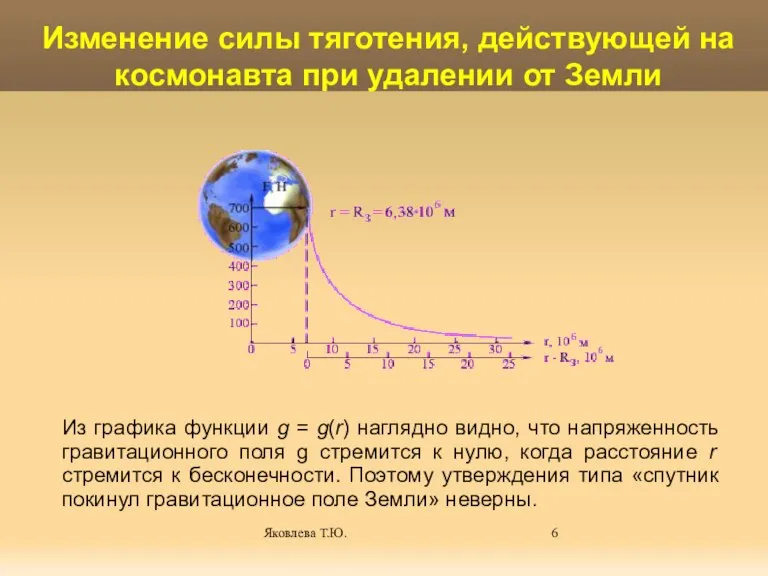
Яковлева Т.Ю.
Изменение силы тяготения, действующей на космонавта при удалении от Земли
Из графика функции g = g(r) наглядно видно, что напряженность гравитационного поля g стремится к нулю, когда расстояние r стремится к бесконечности. Поэтому утверждения типа «спутник покинул гравитационное поле Земли» неверны.

Яковлева Т.Ю.
Расстояние от Земли до Луны
Гравитационные поля небесных тел перекрываются. Если двигаться вдоль прямой, соединяющей центры Земли и Луны, то, начиная с определенного места, будет преобладать напряженность гравитационного поля Луны.

Яковлева Т.Ю.
Средний радиус Земли RЗ ≈ 6,37·106 м. Луна находится от центра Земли на расстоянии rЛ ≈ 3,84·108 м. Следовательно, ускорение aЛ, обусловленное земным притяжением, на орбите Луны равно:
aл = g(Rз/rл)2 = 9,81·(6,37·106 / 3,84·108)2 = 9,81·602 = 0,0027 м/с2.
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является нормальным ускорением, которое можно рассчитать по кинематической формуле для нормального ускорения:
aл = v2/rл = (2πrл/Т)2 / rл = (2πrл /Т)2 / rл =4π2rл / Т 2 = 0,0027 м/с2,
где T – период обращения Луны вокруг Земли (27,3 сут).
Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.
Гравитационное поле Луны

Яковлева Т.Ю.
Одним из проявлений силы взаимного тяготения является сила тяжести, т. е. сила притяжения тел к Земле.
Если на тело действует только сила тяжести, то оно совершает свободное падение. Свободное падение – это движение тела в безвоздушном пространстве (вакууме) под действием только силы тяжести.
Ускорение свободного падения (ускорение силы тяжести) – ускорение, которое приобретает свободная материальная точка под действием силы тяжести. Такое ускорение имел бы центр тяжести любого тела при падении тела на Землю с небольшой высоты в безвоздушном пространстве.
Сила тяжести

Яковлева Т.Ю.
Если сила притяжения в точности пропорциональна массе, то два тела с разной массой должны одинаково изменять свою скорость в поле тяготения. Опыты с ядрами, сброшенными с «Падающей башни» в Пизе в конце XVI в., подтвердили с доступной для того времени точностью, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же.
Опыты Галилея с падающими телами

Яковлева Т.Ю.
Пизанская падающая башня

Яковлева Т.Ю.
Опыты Галилея с падающими телами
Галилео Галилей (1564 — 1642 гг.)

Яковлева Т.Ю.
Кинематические характеристики свободного падения

Яковлева Т.Ю.
Движение тела, брошенного вертикально вверх с начальной скоростью v0

Яковлева Т.Ю.
Тело, вертикально брошенное вверх с уровня Земли (y = 0) со скоростью v0, возвращается на Землю (y = 0) через время
следовательно, время подъёма и время падения одинаковы. Во время падения на Землю скорость тела равна –v0, т. е. тело падает на Землю с такой же по модулю скоростью, с какой оно было брошено вверх.
Движение тела, брошенного вертикально вверх с начальной скоростью v0

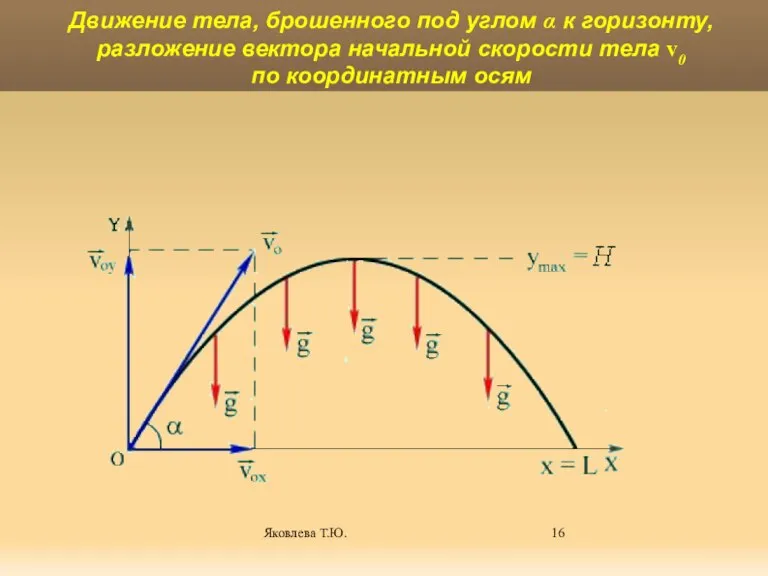
Яковлева Т.Ю.
Движение тела, брошенного под углом α к горизонту, разложение вектора начальной скорости тела v0
по координатным осям

Яковлева Т.Ю.
Движение тела, брошенного под углом α к горизонту
градусов)

Яковлева Т.Ю.
Движение тела, брошенного под углом к горизонту, происходит по параболе. В реальных условиях такое движение в значительной степени искажено из-за сопротивления воздуха, которое может существенно уменьшить дальность полёта тела.
Баллистическая траектория – траектория движения свободно брошенного тела под действием только силы тяжести (траекторию движения такого тела в атмосфере при равном или близком к нулю отношении подъёмной силы к аэродинамическому сопротивлению также называют баллистической траекторией).
Баллистическая траектория