Содержание
- 2. Economic Condition: Developed and less developed countries The Western has far more higher incomes than their
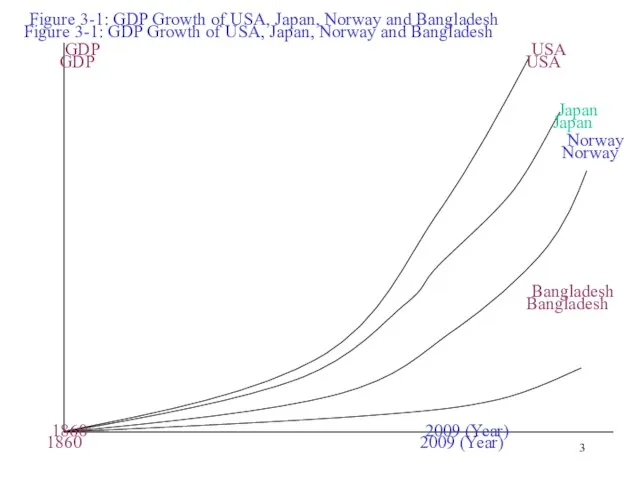
- 3. Figure 3-1: GDP Growth of USA, Japan, Norway and Bangladesh GDP USA Japan Norway Bangladesh 1860
- 4. The Graph above has four characteristics: It shows that in in USA income increased more than
- 5. Question is: What are causes behind these differences? What will determine the standard of living in
- 6. 1. GROWTH ACCOUNTING Growth accounting explains the role of different Factors of production in growth It
- 7. In Equation (1): K = Capital (K) and N = Labour Force A = Level of
- 8. Level of technology The letter “A” in the production function (1) indicates level of ‘productivity’ Higher
- 9. 2. COMPUTING GROWTH OF OUTPUT Production function (1) can be used to explain causes behind the
- 10. (Dividing both side by Y) Following are steps to deduce Growth Accounting Equation (2) from Production
- 11. In Equation (2): (1 - θ) is the share of labour to the GDP θ is
- 12. Example The capital share of income is 25% and that of labour is 75%, which correspond
- 13. 3. ACCOUNTING GROWTH OF PER CAPITA OUTPUT It means to find out on what factors does
- 14. Equation (2) says: ΔY/Y = [(1 - θ) × ΔN/N] + (θ × ΔK/K) + ΔA/A
- 15. Equation (3) says per capita growth rate of GDP depends on: Per capita capital growth (Δk/k
- 16. 4. Accounting Technological Change Let us the growth of GDP, Population Growth and Capital Growth are
- 17. Technological progress cause increase of labour productivity Such progress is called labour stimulating technological progress For
- 18. 5. Cobb-Douglas Production Function Here: θ is share of capital to the GDP [For USA θ
- 19. For labour stimulating technological progress, the Cobb-Douglas Production Function could be written as: In this case
- 20. 6. Empirical Estimate of Growth Capital Growth Robert Solow studied period 1909-1949 in USA and concluded
- 21. 7. Growth Factors Other Than Capital and Labour Other important factors of growth are: Natural resources
- 22. Human Capital In industrialized countries, qualified workers is more important than unqualified labour Stock of unqualified
- 23. Impact of Immigration on Human Capital Immigration boosts per capital output when skilled workers enter in
- 24. Problem # 1 In a simple scenario with only two factors of production, suppose that capital’s
- 25. Problem # 2 Suppose output is growing at 3 percent per year and capital's and labor's
- 26. Problem # 3 Suppose that capital's and labor's shares of income are 0.3 and 0.7. What
- 27. Problem Consider the following production function: Y = K.5 (AN).5, where both the capital and the
- 28. Questions Explain with mathematical model on which factor the growth of the economy depends. What for
- 29. Questions How do you express growth of per capita GDP using Cobb Douglas production function? Discuss
- 31. Скачать презентацию











![Equation (2) says: ΔY/Y = [(1 - θ) × ΔN/N] + (θ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/374621/slide-13.jpg)















 Своя игра, хореография
Своя игра, хореография 2 день. Награждение партнеров
2 день. Награждение партнеров Притча
Притча Подача заявления в 1-й класс в электронном виде
Подача заявления в 1-й класс в электронном виде анатомия и физ 1
анатомия и физ 1 о Польше
о Польше Правила безопасности при работе с иглой
Правила безопасности при работе с иглой Notstromaggregat Steuerschrank
Notstromaggregat Steuerschrank Презентация на тему СТЕКЛЯННЫЕ ТОВАРЫ
Презентация на тему СТЕКЛЯННЫЕ ТОВАРЫ  Теневая экономика
Теневая экономика Презентация на тему Внешнее и внутреннее строение листа
Презентация на тему Внешнее и внутреннее строение листа Spotlight - 3
Spotlight - 3 КАЧЕСТВО ЖЕЛЕЗНОДОРОЖНЫХ ТРАНСПОРТНЫХ УСЛУГ
КАЧЕСТВО ЖЕЛЕЗНОДОРОЖНЫХ ТРАНСПОРТНЫХ УСЛУГ Основные направления византийского стиля живописи
Основные направления византийского стиля живописи Динамика уровня экономического и социального развития Санкт-Петербурга
Динамика уровня экономического и социального развития Санкт-Петербурга Культура Древней Руси
Культура Древней Руси investitsii_4
investitsii_4 Sport in our life
Sport in our life Презентация на тему Конструкция used to
Презентация на тему Конструкция used to Центр развития (www.dcenter.ru)
Центр развития (www.dcenter.ru) Страны-countries
Страны-countries Избирательное право
Избирательное право «Использование информационных компьютерных технологий на учебных занятиях по биологии как средство повышения эффективности уч
«Использование информационных компьютерных технологий на учебных занятиях по биологии как средство повышения эффективности уч Центр развития творчества детей и юношества р.п. Переяславка
Центр развития творчества детей и юношества р.п. Переяславка Пенсионная система в Казахстане
Пенсионная система в Казахстане Презентация на тему Семена
Презентация на тему Семена Дворницкая+охрана+общепит
Дворницкая+охрана+общепит Кадровая политика как основа для принятия кадровых решений
Кадровая политика как основа для принятия кадровых решений