Индивидуальное задание по математической логике

Четкие шаги нечеткой логики

План:
Немного истории;
Нечеткая логика;
Нечеткие подмножества;
Операции над нечеткими подмножествами;
Свойства множества нечетких подмножеств;
Нечеткая логика высказываний;
Нечеткие релейно-контактные схемы;
Математический аппарат;
Не четкий логический вывод.

Основатель теории
Американский ученый
Лотфи Заде
(Lotfi Zadeh)

Последователь и ученик Л. Заде
Барт Коско
(Bart Kosko)
В своей знаменитой теореме FAT («Fuzzy Approximation Theorem») доказал, что любая математическая система может быть аппроксимирована системой, основанной на «нечеткой логике».

Революция
Японское правительство финансировало 5-летнюю программу по «нечеткой логике».
Первый же год использования новой системы принес банку $770 000 в месяц только объявленной прибыли.
«Motorola», «General Electric», «Otis Elevator», «Pacific Gas & Electric», «Ford» и другие в начале 90-х начали инвестировать программы дальнейших разработок в этом направлении.

Нечеткая логика отличается от двузначной классической логики тем, что допускает континуальное число истинностных значений для высказываний. В простейшем случае эти значения принадлежат отрезку [0,1] действительных чисел.

Нечеткие подмножества
Нечеткое подмножество множества Е – это множество пар вида:
Где - функция.
Множество М называется множеством принадлежности, а функция
- функцией принадлежности.
Пара
интерпретируется как элемент ,
который принадлежит подмножеству
со степенью

Операции над нечеткими множествами:

Объединение:
Объединение нечетких множеств и - это нечеткое множество
для которого

Пересечение:
Аналогично имеем пересечение нечетких множеств и ,
если по определению

Дополнение:
Нечеткое множество есть дополнение для ,т.е.
если

Включение:
Если даны нечеткие множества и , то пишем тогда и только тогда, когда

Свойства множества нечетких подмножеств:

Однако
которые для обычных множеств имеют вид
и справедливы.

Нечеткая логика высказываний
Нечеткие пропозициональные переменные - это
Полагаем, что

Нечеткие логические операции

Введем понятие нечеткой формулы:
1)нечеткая пропозициональная переменная есть (атомарная) нечеткая формула;
2)если А и В нечеткие формулы, то
нечеткие формулы;
3)если А - нечеткая формула, то ¬А – нечеткая формула.

Свойства нечетких логических операций:

Однако
Таким образом, нечеткая логика не является классической.

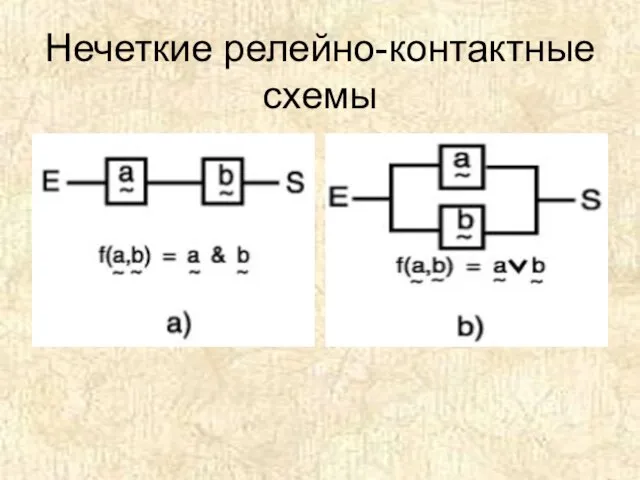
Нечеткие релейно-контактные схемы

Наиболее распространенные типовые формы кривых для задания функций принадлежности: треугольная, трапецеидальная и гауссова.

Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:

Для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):

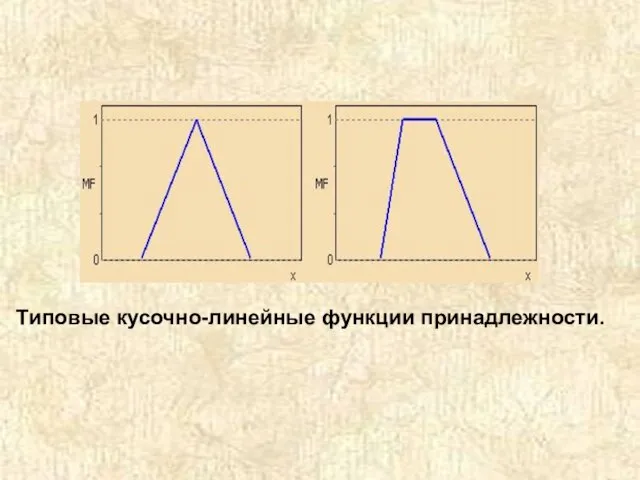
Типовые кусочно-линейные функции принадлежности.

Функция принадлежности гауссова типа описывается формулой

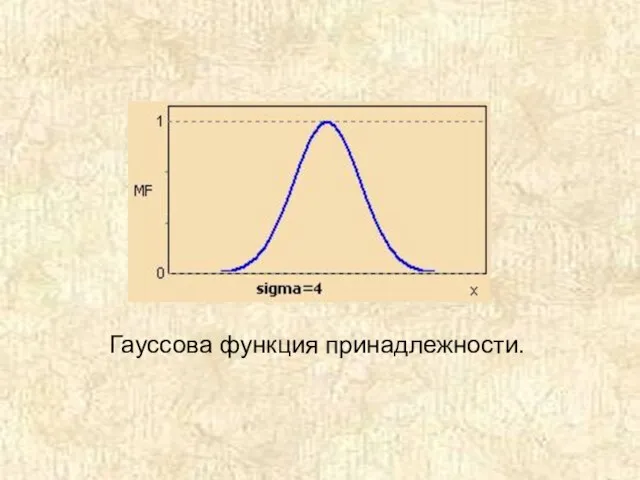
Гауссова функция принадлежности.

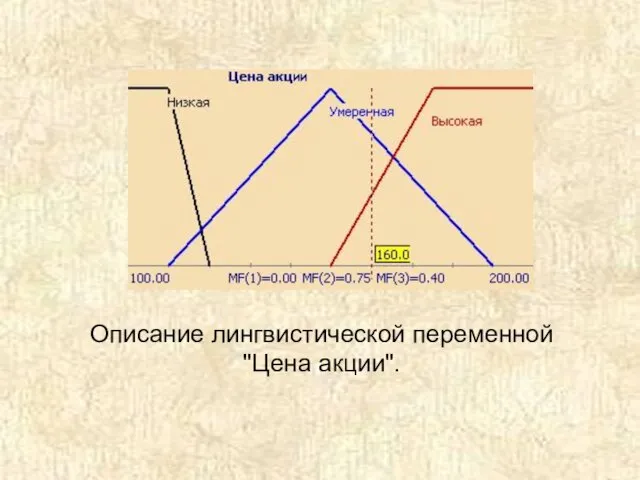
Описание лингвистической переменной
"Цена акции".

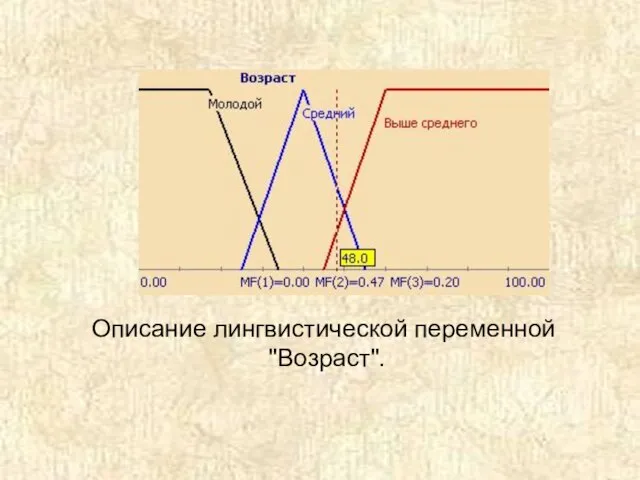
Описание лингвистической переменной
"Возраст".

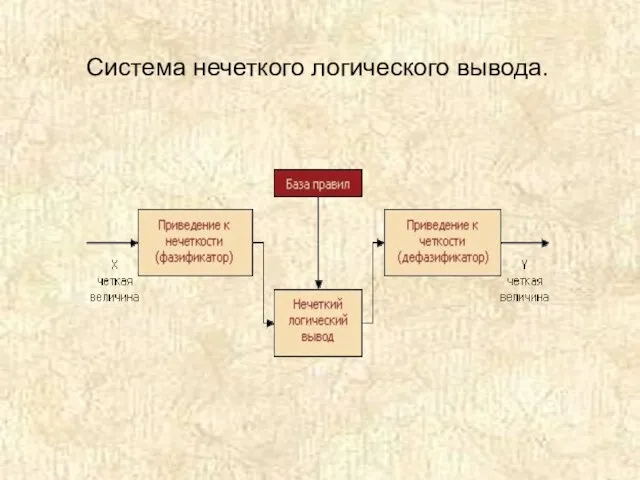
Система нечеткого логического вывода.

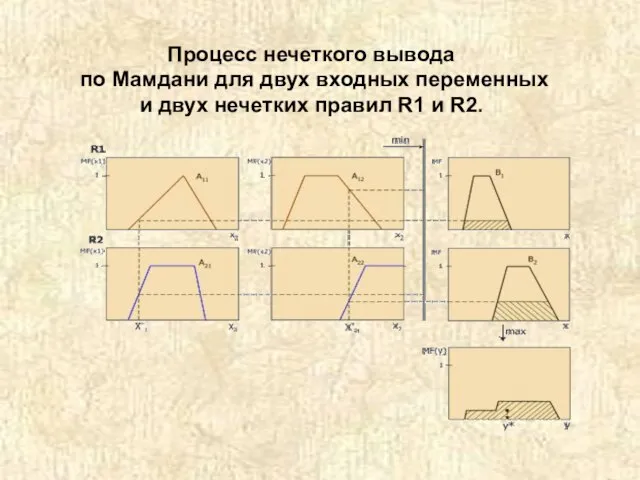
Процесс нечеткого вывода
по Мамдани для двух входных переменных
и двух нечетких правил R1 и R2.