Содержание
- 2. Слайд 2 Основы элементной базы цифровых автоматов Для согласования параметров элементов ТТЛ и И2Л на входах
- 3. Слайд 3 ; Большинство схем трансляторов имеет существенно более высокие значения потребляемой мощности Pкр и площади
- 4. Слайд 4 3 ПРЕОБРАЗОВАТЕЛЬНЫЕ УСТРОЙСТВА Преобразовательные устройства – это функциональные узлы комбинационного типа: преобразователи кодов, мультиплексоры
- 5. Слайд 5 3.1.1 Преобразование прямого кода в обратный Преобразование прямого кода в обратный реализуется сложением по
- 6. Слайд 6 Рисунок 3.1 – Схемы преобразователей прямого кода в обратный (а), дополнительный (б) и кода
- 7. Слайд 7 Таблица 3.1 – Преобразования двоично-десятичных кодов Условное обозначение преобразователя кодов показано на рисунке 3.2,
- 8. Слайд 8 Рисунок 3.2 – Условное обозначение преобразователя кодов (а), и схемы преобразователей для двух (б)
- 9. Слайд 9 Выше была для краткости приведена лишь часть таблицы функционирования шестиразрядного преобразователя, однако при необходимости
- 10. Слайд 10 (см. таблицу функционирования для обоих преобразований, имеющую следующий вид): Таблица 3.2 – Преобразование двоично-десятичного
- 11. Слайд 11 При работе в режимах преобразования двоично-десятичного кода в дополнение до 9 или 10 вход
- 12. Слайд 12 3.1.3 Преобразователи одного кода в другой Широкое применение в вычислительной технике находят преобразователи кодов,
- 13. Слайд 13 Таблица 3.3 – Преобразование одного кода в другой Рассмотрим построение преобразователя кода 8421 в
- 14. Слайд 14 3.1.4 Программируемая логическая матрица (ПЛМ) ПЛМ – комбинационная ЦИМ, предназначенная для преобразования кодов, выполнения
- 15. Слайд 15 3.2 Дешифраторы и шифраторы Дешифраторы и шифраторы по существу принадлежат к числу преобразователей кодов.
- 16. Слайд 16 3.2.1.1 Линейные дешифраторы Линейные дешифраторы представляют собой совокупность схем И, формирующих управляющий сигнал только
- 17. Слайд 17 В дешифраторах часто предусматривается операция стробирования (тактирования), разрешающая выработку выходных сигналов только в определенных
- 18. Слайд 18 Одноступенчатый дешифратор – наиболее быстродействующий, но его реализация при значительной разрядности входного слова затруднена,
- 19. Слайд 19 3.2.1.2 Пирамидальные дешифраторы Пирамидальные дешифраторы на n входов имеют x=n-1 ступеней, причем на каждой
- 20. Слайд 20 3.2.1.3 Прямоугольные дешифраторы В прямоугольных дешифраторах n его входов разбиваются на две группы по
- 21. Слайд 21 3.2.1.4 Схема наращивания размерности дешифраторов ЦИМ дешифраторов в настоящее время имеют три входа (серии
- 22. Слайд 22 Рисунок 3.10 – Схема наращивания размерности дешифраторов
- 23. Слайд 23 3.2.2 Шифраторы Шифраторы – устройства, осуществляющие преобразование десятичных чисел в двоичный код. Шифратор содержит
- 24. Слайд 24 Рисунок 3.11 – Схема ввода данных с клавиатуры (а) и дешифратор «10х4» (б) Для
- 25. Слайд 25 Для указания старшей единицы (поиск разряда слова) используют шифраторы приоритета (рисунок 3.12). На вход
- 26. Слайд 26 Указатели старшей единицы с выходом в коде «один из N» можно получить путем дешифрации
- 27. Слайд 27 3.3 Мультиплексоры – демультиплексоры 3.3.1 Мультиплексоры Мультиплексор – коммутатор логических сигналов, обеспечивающий передачу информации,
- 28. Слайд 28 3.14 – Принцип работы мультиплексора (а), принцип реализации (б) Рисунок 3.15 – Схема мультиплексора
- 29. Слайд 29 В сериях микросхем встречаются мультиплексоры «4>1», «8>1», «16>1» Мультиплексоры на большее число входов, как
- 30. Слайд 30 Рисунок 3.16 – Наращивание размерности мультиплексора Рисунок 3.17 – Наращивание размерности мультиплексора, имеющего выходные
- 31. Слайд 31 3.3.2 Демультиплексоры Демультиплексор – коммутатор логических сигналов, обеспечивающий передачу информации, поступающей по одному входу,
- 33. Скачать презентацию
Слайд 2Слайд 2
Основы элементной базы цифровых автоматов
Для согласования параметров элементов ТТЛ и И2Л
Слайд 2
Основы элементной базы цифровых автоматов
Для согласования параметров элементов ТТЛ и И2Л

Рисунок 2.4 – Входной (а) и выходной (б) трансляторы И2Л
Сопротивление R0, R1 выбираются из условия отпирания транзистора VT1 при Uвх=U1вх. Выходным транслятором служит элемент И2Л с подключенным внешним резистором Rв (рисунок 2.4, б), сопротивление которого выбирается из условия:
(2.3)
Слайд 3Слайд 3
;
Большинство схем трансляторов имеет существенно более высокие значения потребляемой мощности Pкр и площади Акр,
Слайд 3
;
Большинство схем трансляторов имеет существенно более высокие значения потребляемой мощности Pкр и площади Акр,

(2.4)
(2.5)
Слайд 4Слайд 4
3 ПРЕОБРАЗОВАТЕЛЬНЫЕ УСТРОЙСТВА
Преобразовательные устройства – это функциональные узлы комбинационного типа: преобразователи
Слайд 4
3 ПРЕОБРАЗОВАТЕЛЬНЫЕ УСТРОЙСТВА
Преобразовательные устройства – это функциональные узлы комбинационного типа: преобразователи

3.1 Преобразователи кодов
Преобразователи кодов изменяют вид кодирования данных. В ЭВМ, цифровой технике используют несколько форм представления информации. Входные и выходные устройства оперируют с привычными человеку десятичными кодами, вычисления ведутся в двоичных кодах, промежуточной формой представления чисел служит двоично-десятичный код. Используют и другие представления данных. В широком смысле слова к преобразователям кодов можно отнести многие цифровые устройства, в частности шифраторы и дешифраторы, однако по традиции эти устройства выделены в отдельные классы.
Двоичные числа могут быть представлены в прямом, обратном или дополнительном кодах
Слайд 5Слайд 5
3.1.1 Преобразование прямого кода в обратный
Преобразование прямого кода в обратный реализуется сложением по
Слайд 5
3.1.1 Преобразование прямого кода в обратный
Преобразование прямого кода в обратный реализуется сложением по

3.1.2 Преобразование прямого кода в дополнительный
Преобразование прямого кода в дополнительный (дополнение числа до 2n) реализуется сложнее. В этом случае операция преобразования не является поразрядной, и для определения значения кода в каком-либо разряде требуется анализ значений других разрядов. Для получения дополнительного кода нужно проинвертировать все разряды преобразуемого кода и затем прибавить к результату единицу (рисунок 3.1, б).
Слайд 6Слайд 6
Рисунок 3.1 – Схемы преобразователей прямого кода в обратный (а), дополнительный
Слайд 6
Рисунок 3.1 – Схемы преобразователей прямого кода в обратный (а), дополнительный
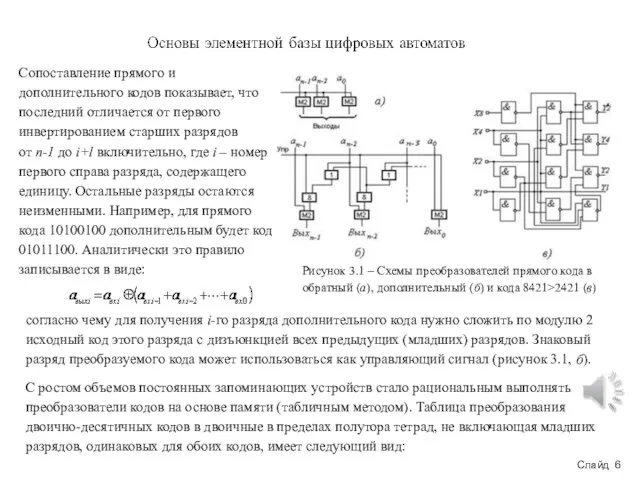
Сопоставление прямого и дополнительного кодов показывает, что последний отличается от первого инвертированием старших разрядов от n-1 до i+l включительно, где i – номер первого справа разряда, содержащего единицу. Остальные разряды остаются неизменными. Например, для прямого кода 10100100 дополнительным будет код 01011100. Аналитически это правило записывается в виде:
согласно чему для получения i-гo разряда дополнительного кода нужно сложить по модулю 2 исходный код этого разряда с дизъюнкцией всех предыдущих (младших) разрядов. Знаковый разряд преобразуемого кода может использоваться как управляющий сигнал (рисунок 3.1, б).
С ростом объемов постоянных запоминающих устройств стало рациональным выполнять преобразователи кодов на основе памяти (табличным методом). Таблица преобразования двоично-десятичных кодов в двоичные в пределах полутора тетрад, не включающая младших разрядов, одинаковых для обоих кодов, имеет следующий вид:
Слайд 7Слайд 7
Таблица 3.1 – Преобразования двоично-десятичных кодов
Условное обозначение преобразователя кодов показано на
Слайд 7
Таблица 3.1 – Преобразования двоично-десятичных кодов
Условное обозначение преобразователя кодов показано на
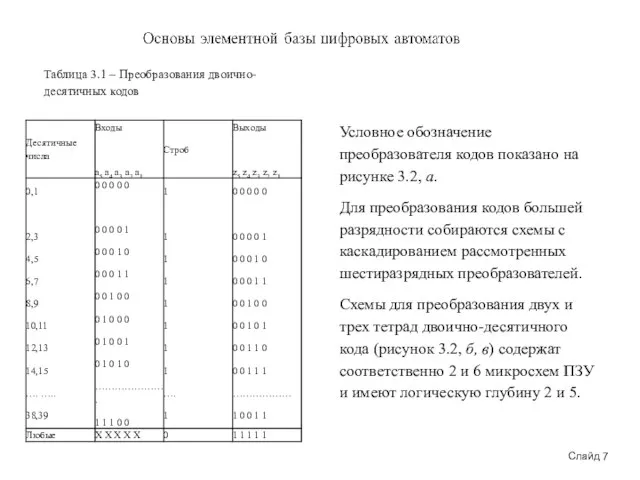
Для преобразования кодов большей разрядности собираются схемы с каскадированием рассмотренных шестиразрядных преобразователей.
Схемы для преобразования двух и трех тетрад двоично-десятичного кода (рисунок 3.2, б, в) содержат соответственно 2 и 6 микросхем ПЗУ и имеют логическую глубину 2 и 5.
Слайд 8Слайд 8
Рисунок 3.2 – Условное обозначение преобразователя кодов (а), и схемы преобразователей
Слайд 8
Рисунок 3.2 – Условное обозначение преобразователя кодов (а), и схемы преобразователей
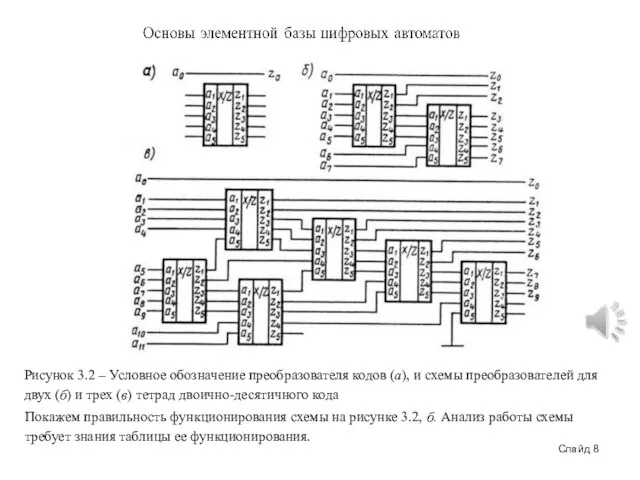
Покажем правильность функционирования схемы на рисунке 3.2, б. Анализ работы схемы требует знания таблицы ее функционирования.
Слайд 9Слайд 9
Выше была для краткости приведена лишь часть таблицы функционирования шестиразрядного преобразователя,
Слайд 9
Выше была для краткости приведена лишь часть таблицы функционирования шестиразрядного преобразователя,

Возьмем для примера число 55, которое в двоично-десятичном коде выражается словом 01010101 и в двоичном коде словом 00110111. На рисунке 3.3 показаны сигналы, появляющиеся па выходах и входах шестиразрядных преобразователей при подаче на схему двоично-десятичного кода числа 55, свидетельствующие о правильности функционирования схемы.
С помощью каскадирования строятся и схемы большей разрядности. При этом для преобразователя шести тетрад, например, требуется 28 микросхем, а логическая глубина схемы равна 13.
Рисунок 3.3 – Пример преобразования конкретного кода
Выше отмечено, что для преобразователя двоично-десятичного кода в двоичный в пределах полутора тетрад остаются избыточными три выхода ПЗУ. Это позволяет дополнительно реализовать на той же микросхеме преобразование двоично-десятичных кодов в обратные или дополнительные в пределах одной тетрады. Нехватка одного выхода не препятствует решению указанных задач, так как в обоих случаях один из разрядов оказывается одинаковым для входных и выходных кодов
Слайд 10Слайд 10
(см. таблицу функционирования для обоих преобразований, имеющую следующий вид):
Таблица 3.2 –
Слайд 10
(см. таблицу функционирования для обоих преобразований, имеющую следующий вид):
Таблица 3.2 –
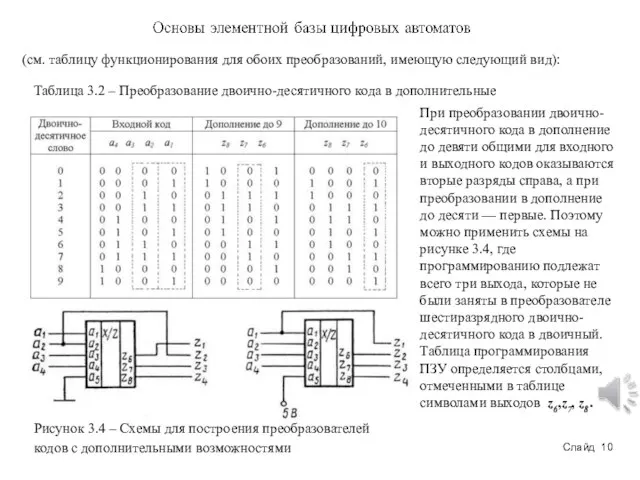
При преобразовании двоично-десятичного кода в дополнение до девяти общими для входного и выходного кодов оказываются вторые разряды справа, а при преобразовании в дополнение до десяти — первые. Поэтому можно применить схемы на рисунке 3.4, где программированию подлежат всего три выхода, которые не были заняты в преобразователе шестиразрядного двоично-десятичного кода в двоичный. Таблица программирования ПЗУ определяется столбцами, отмеченными в таблице символами выходов z6,z7, z8.
Рисунок 3.4 – Схемы для построения преобразователей кодов с дополнительными возможностями
Слайд 11Слайд 11
При работе в режимах преобразования двоично-десятичного кода в дополнение до 9
Слайд 11
При работе в режимах преобразования двоично-десятичного кода в дополнение до 9

На ПЗУ реализуются и преобразователи двоичных кодов в двоично-десятичные. При этом на входе можно задать шестиразрядные коды (пять входов имеет ПЗУ, а младший разряд — общий для обоих кодов и не нуждается в преобразовании) и получить на выходе двоично-десятичный код в пределах полутора тетрад. Для преобразования слов большей разрядности составляются схемы из нескольких шестиразрядных преобразователей
Слайд 12Слайд 12
3.1.3 Преобразователи одного кода в другой
Широкое применение в вычислительной технике находят
Слайд 12
3.1.3 Преобразователи одного кода в другой
Широкое применение в вычислительной технике находят

Особенность кода Грея состоит в том, что при переходе к каждому последующему в коде изменяется значение только одного двоичного разряда. В коде Джонсона переход к последующему числу осуществляется путём последовательной замены 0 на, начиная справа до заполнения всех разрядов 1, а затем заменой 1 на 0, до заполнения нулями. Коды с дополнением до 9, 10 с «избытком 9» используются для выполнения сложения и вычитания двоично-десятичных чисел. Для преобразования кодов можно пользоваться двумя методами: методом, основанным на преобразовании исходного двоичного кода в десятичный и последующего преобразования десятичного представления в требуемый двоичный код; метод синтеза логического устройства комбинационного типа непосредственно реализующего данное преобразование.
Слайд 13Слайд 13
Таблица 3.3 – Преобразование одного кода в другой
Рассмотрим построение преобразователя кода
Слайд 13
Таблица 3.3 – Преобразование одного кода в другой
Рассмотрим построение преобразователя кода

Рисунок 3.5 – Логическая схема преобразователя кодов 8421 в 2421 на элементах И-НЕ
Слайд 14Слайд 14
3.1.4 Программируемая логическая матрица (ПЛМ)
ПЛМ – комбинационная ЦИМ, предназначенная для преобразования
Слайд 14
3.1.4 Программируемая логическая матрица (ПЛМ)
ПЛМ – комбинационная ЦИМ, предназначенная для преобразования

Рисунок 3.6 – Функциональная и принципиальная
электрическая схема ПЛМ на n-МОП транзисторах
Слайд 15Слайд 15
3.2 Дешифраторы и шифраторы
Дешифраторы и шифраторы по существу принадлежат к числу
Слайд 15
3.2 Дешифраторы и шифраторы
Дешифраторы и шифраторы по существу принадлежат к числу

3.2.1 Дешифраторы
Дешифраторы – устройства, предназначенные для преобразования двоичного n-разрядного кода в комбинацию управляющих сигналов.
В условных обозначениях дешифраторов и шифраторов используются буквы DC и CD (от слов decoder и coder соответственно). Двоичные дешифраторы преобразуют двоичный код в код «1 из N». Иными словами, в зависимости от входного кода на выходе возбуждается одна из цепей. Так как с помощью n-разрядного двоичного кода можно отобразить 2п кодовых комбинаций, число выходов полного дешифратора равно 2п.Если часть входных наборов не используется, то дешифратор называют неполным и у него Nвых<2n.
Функционирование дешифратора описывается системой логических выражений вида:
где mi – минтермы п входных переменных.
В зависимости от разрядности дешифруемого кода и функциональных возможностей логических интегральных схем дешифратор можно выполнить на основе одноступенчатой (или линейной) и многоступенчатой схем дешифрации. Среди многоступенчатых схем можно выделить прямоугольные (матричные) и пирамидальные схемы построения дешифраторов. Дешифраторы широко используются в устройствах вывода информации и управления
Слайд 16Слайд 16
3.2.1.1 Линейные дешифраторы
Линейные дешифраторы представляют собой совокупность схем И, формирующих управляющий
Слайд 16
3.2.1.1 Линейные дешифраторы
Линейные дешифраторы представляют собой совокупность схем И, формирующих управляющий

Рисунок 3.7 – Линейный дешифратор на два входа
Поэтому дешифраторы часто называют избирательными схемами. Функционирование дешифратора можно описать с помощью таблицы истинности (таблица 3.4) или логических функций:
Таблица 3.4 – Таблица истинности
где X1, X2, ..., Xn; Y0,Y1, ...,Y2n-1 – сигналы на входах и выходах дешифратора. Для линейного дешифратора на n входов требуется элементов И с n входами, Линейные дешифраторы наиболее эффективны, когда разрядность входного кода n не превышает число n входов схемы И типовом элемента ЦИМ. Быстродействие линейных дешифраторов является наибольшим по сравнению с другими схемами дешифрации, так как время установления tуст управляющего сигнала на входе дешифратора равно средней задержке tзд.сртипового элемента ЦИМ (tуст=tзд.ср). Основной недостаток – требуется большая нагрузочная способность элементов регистра (триггеров), к которым подключаются входы дешифраторов, равная mтр=2n-1.
Слайд 17Слайд 17
В дешифраторах часто предусматривается операция стробирования (тактирования), разрешающая выработку выходных сигналов
Слайд 17
В дешифраторах часто предусматривается операция стробирования (тактирования), разрешающая выработку выходных сигналов

Описанные варианты можно назвать стробированием по выходу и стробированием по входу.
Время установления выходного сигнала т.к. при изменении состояния дешифратора на одном из выходов сигнал возбуждения появляется, а на другом — исчезает. При стробировании по выходу задержка относительно начала разрешающего сигнала
составляет а при стробировании по входу
Нагрузка, создаваемая дешифратором на источник сигналов, вычисляется с учетом того, что каждая переменная присутствует на входе каждого элемента в прямом либо инверсном виде, причем оба вида используются в равной мере. Следовательно, к источникам сигналов
и будет подключено число входов
Слайд 18Слайд 18
Одноступенчатый дешифратор – наиболее быстродействующий, но его реализация при значительной разрядности
Слайд 18
Одноступенчатый дешифратор – наиболее быстродействующий, но его реализация при значительной разрядности

При построении прямоугольного двухступенчатого дешифратора для его реализации требуется
общее количество схем И, определяемая из выражений при n четном и
при n нечетном. При этом требуется 2n двухвходовых схем И для матричного дешифратора, 2x x- входовых схем для первого линейного дешифратора и 2n-x (n-x)– входовых схем И для второго линейного дешифратора. При n>4 прямоугольные дешифраторы примерно в 2 раза экономичнее пирамидальных. Следует отметить, что к нагрузочной способности ЦИМ предконечной ступени прямоугольных дешифраторов предъявляются достаточно высокие требования, т.е.
Слайд 19Слайд 19
3.2.1.2 Пирамидальные дешифраторы
Пирамидальные дешифраторы на n входов имеют x=n-1 ступеней, причем на каждой ступени
Слайд 19
3.2.1.2 Пирамидальные дешифраторы
Пирамидальные дешифраторы на n входов имеют x=n-1 ступеней, причем на каждой ступени

Недостаток пирамидальных дешифраторов: различные входы дешифраторов оказывают неравномерную нагрузку на элементы регистров, а большое число ступеней снижает его быстродействие tуст=xtзд.ср.
Рисунок 3.8 – Пирамидальный дешифратор
Слайд 20Слайд 20
3.2.1.3 Прямоугольные дешифраторы
В прямоугольных дешифраторах n его входов разбиваются на две группы по n/2 переменных
Слайд 20
3.2.1.3 Прямоугольные дешифраторы
В прямоугольных дешифраторах n его входов разбиваются на две группы по n/2 переменных
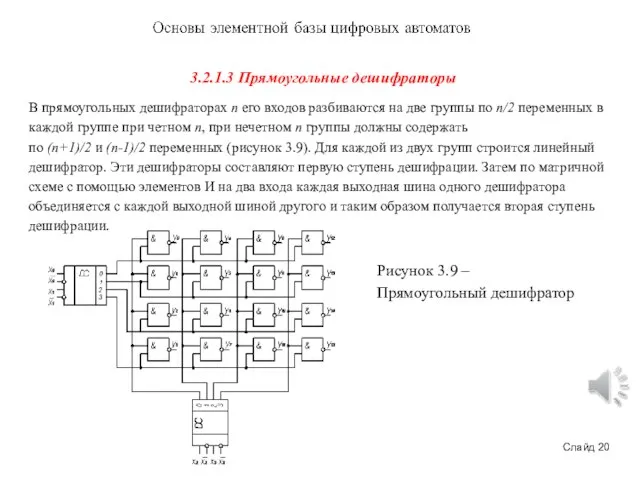
Рисунок 3.9 – Прямоугольный дешифратор
Слайд 21Слайд 21
3.2.1.4 Схема наращивания размерности дешифраторов
ЦИМ дешифраторов в настоящее время имеют три
Слайд 21
3.2.1.4 Схема наращивания размерности дешифраторов
ЦИМ дешифраторов в настоящее время имеют три

В неполных дешифраторах часть входных наборов не является рабочей (не используется). Это обстоятельство можно рассматривать как возможность упрощения дешифратора — нерабочим наборам можно поставить в соответствие любое значение выходов.
Слайд 22Слайд 22
Рисунок 3.10 – Схема наращивания размерности дешифраторов
Слайд 22
Рисунок 3.10 – Схема наращивания размерности дешифраторов

Слайд 23Слайд 23
3.2.2 Шифраторы
Шифраторы – устройства, осуществляющие преобразование десятичных чисел в двоичный код. Шифратор
Слайд 23
3.2.2 Шифраторы
Шифраторы – устройства, осуществляющие преобразование десятичных чисел в двоичный код. Шифратор

Двоичные шифраторы преобразуют код «1 из N» в двоичный код, т. е. выполняют микрооперацию, обратную микрооперации дешифраторов. При возбуждении одной из входных цепей шифратора на его выходах формируется слово, отображающее номер возбужденной цепи. Полный двоичный шифратор имеет 2n входов и п выходов. Одно из основных применений шифратора – ввод данных с клавиатуры, при котором нажатие клавиши с десятичной цифрой должно приводить к передаче в устройство двоичного кода данной цифры (тетрады двоично-десятичного кода). В этом случае нужен неполный шифратор «10х4» (рисунок 3.11, а), на примере которого рассмотрим принципы построения шифраторов.
Из таблицы 3.5 следует, что
Таблица 3.5 – Таблица функционирования шифратора
Слайд 24Слайд 24
Рисунок 3.11 – Схема ввода данных с клавиатуры (а) и дешифратор
Слайд 24
Рисунок 3.11 – Схема ввода данных с клавиатуры (а) и дешифратор
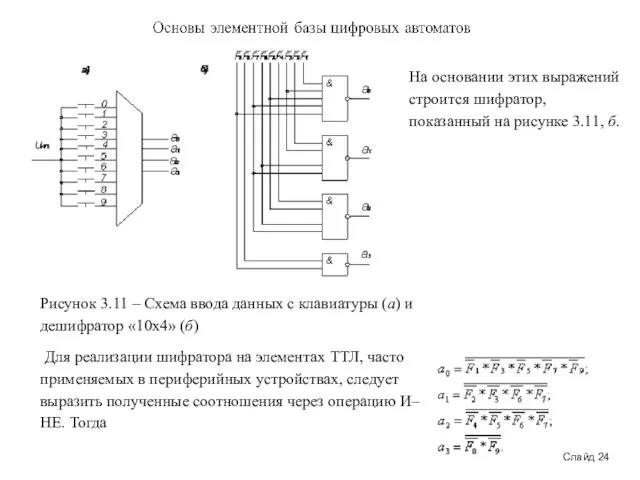
Для реализации шифратора на элементах ТТЛ, часто применяемых в периферийных устройствах, следует выразить полученные соотношения через операцию И–НЕ. Тогда
На основании этих выражений строится шифратор, показанный на рисунке 3.11, б.
Слайд 25Слайд 25
Для указания старшей единицы (поиск разряда слова) используют шифраторы приоритета (рисунок
Слайд 25
Для указания старшей единицы (поиск разряда слова) используют шифраторы приоритета (рисунок

Рисунок 3.12 – Упрощенная схема шифратора приоритета
Слайд 26Слайд 26
Указатели старшей единицы с выходом в коде «один из N» можно получить
Слайд 26
Указатели старшей единицы с выходом в коде «один из N» можно получить
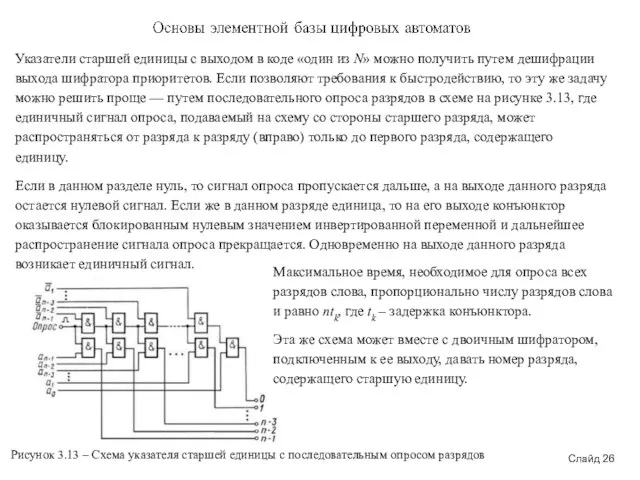
Если в данном разделе нуль, то сигнал опроса пропускается дальше, а на выходе данного разряда остается нулевой сигнал. Если же в данном разряде единица, то на его выходе конъюнктор оказывается блокированным нулевым значением инвертированной переменной и дальнейшее распространение сигнала опроса прекращается. Одновременно на выходе данного разряда возникает единичный сигнал.
Рисунок 3.13 – Схема указателя старшей единицы с последовательным опросом разрядов
Максимальное время, необходимое для опроса всех разрядов слова, пропорционально числу разрядов слова и равно ntk, где tk – задержка конъюнктора.
Эта же схема может вместе с двоичным шифратором, подключенным к ее выходу, давать номер разряда, содержащего старшую единицу.
Слайд 27Слайд 27
3.3 Мультиплексоры – демультиплексоры
3.3.1 Мультиплексоры
Мультиплексор – коммутатор логических сигналов, обеспечивающий передачу
Слайд 27
3.3 Мультиплексоры – демультиплексоры
3.3.1 Мультиплексоры
Мультиплексор – коммутатор логических сигналов, обеспечивающий передачу

Слайд 28Слайд 28
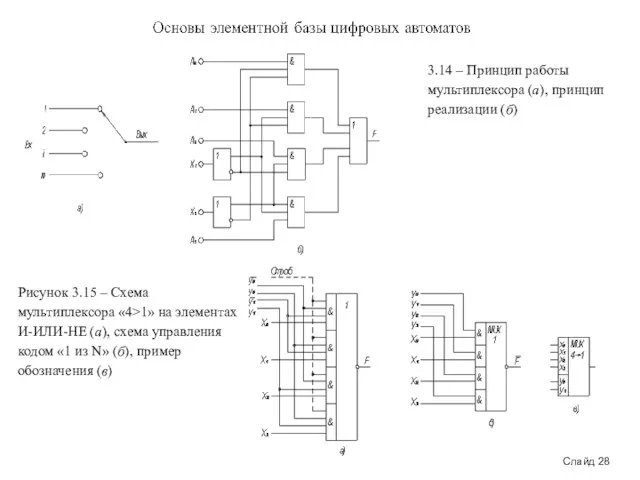
3.14 – Принцип работы мультиплексора (а), принцип реализации (б)
Рисунок 3.15 –
Слайд 28
3.14 – Принцип работы мультиплексора (а), принцип реализации (б)
Рисунок 3.15 –
Слайд 29Слайд 29
В сериях микросхем встречаются мультиплексоры «4>1», «8>1», «16>1» Мультиплексоры на большее
Слайд 29
В сериях микросхем встречаются мультиплексоры «4>1», «8>1», «16>1» Мультиплексоры на большее

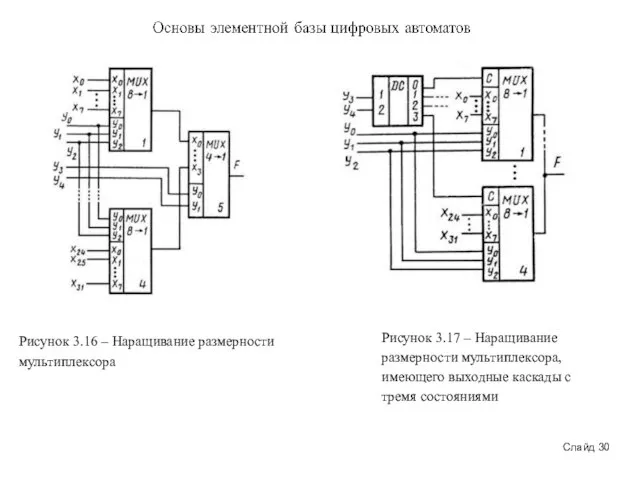
Слайд 30Слайд 30
Рисунок 3.16 – Наращивание размерности мультиплексора
Рисунок 3.17 – Наращивание размерности мультиплексора,
Слайд 30
Рисунок 3.16 – Наращивание размерности мультиплексора
Рисунок 3.17 – Наращивание размерности мультиплексора,
Слайд 31Слайд 31
3.3.2 Демультиплексоры
Демультиплексор – коммутатор логических сигналов, обеспечивающий передачу информации, поступающей по
Слайд 31
3.3.2 Демультиплексоры
Демультиплексор – коммутатор логических сигналов, обеспечивающий передачу информации, поступающей по

где mi – минтермы n адресующих переменных.
В условных изображениях демультиплексор обозначается буквами ДМХ (рисунок 3.18, в). Применительно к мультиплексорам и демультиплексорам пользуются также термином «селекторы данных». Функционирование демультиплексора можно заменить таблицей. Например работу демультиплексора с четырьмя выходами (таблица 3.6). При большом числе входов, при необходимости, может быть построено демультиплексорное дерево (рисунок 3.19). Дешифраторы со стробированием (см. рисунок 3.5, а) можно использовать в качестве демультиплексоров. При этом стробирующий вход выполняет функции информационного входа.
 Рейтинг популярности услуг аутсорсинга среди иностранных компаний, представленных в России Совместный проект аутсорсингового п
Рейтинг популярности услуг аутсорсинга среди иностранных компаний, представленных в России Совместный проект аутсорсингового п Разработка стратегии развертывания приложений
Разработка стратегии развертывания приложений Собственная и примесная проводимость полупроводников
Собственная и примесная проводимость полупроводников  Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)
Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)  Расчеты по уравнениям реакций, протекающих в растворах
Расчеты по уравнениям реакций, протекающих в растворах Презентация на тему Моя снежинка не растает
Презентация на тему Моя снежинка не растает Календарь-трансформер
Календарь-трансформер Становись партнером и зарабатывай с продажи билетов
Становись партнером и зарабатывай с продажи билетов Типовые приемы в консультировании
Типовые приемы в консультировании Презентация на тему Одежда Средних веков (5 класс)
Презентация на тему Одежда Средних веков (5 класс) Презентация на тему Военные года 1941-1945
Презентация на тему Военные года 1941-1945  Принципы осуществления радиосвязи
Принципы осуществления радиосвязи ООО Алми. Строительная компания
ООО Алми. Строительная компания Алиаскарова Ж.А. Человек науки
Алиаскарова Ж.А. Человек науки Стили речи. Введение в стилистику
Стили речи. Введение в стилистику Исследование и разработка направленного ответвителя с улучшенными характеристиками
Исследование и разработка направленного ответвителя с улучшенными характеристиками Auto Lux. Расширяем возможности микс системы. Набор специальных пигментов от кампании Примо Колор
Auto Lux. Расширяем возможности микс системы. Набор специальных пигментов от кампании Примо Колор СБЕРБАНК ЛИЗИНГ НОВЫЕ ВОЗМОЖНОСТИСЕГОДНЯ
СБЕРБАНК ЛИЗИНГ НОВЫЕ ВОЗМОЖНОСТИСЕГОДНЯ Призер муниципального этапа всероссийской олимпиады школьников по физической культуре Бушковский Никита
Призер муниципального этапа всероссийской олимпиады школьников по физической культуре Бушковский Никита Уважаемые коллеги! От имени коллектива НП Национальная страховая гильдия » примите искренние поздравления с профессиональным
Уважаемые коллеги! От имени коллектива НП Национальная страховая гильдия » примите искренние поздравления с профессиональным  Конспект занятия по развитию речив подготовительной группе детского сада на тему: «Музей почтовых принадлежностей» (с использов
Конспект занятия по развитию речив подготовительной группе детского сада на тему: «Музей почтовых принадлежностей» (с использов Функции русского языка в современном мире
Функции русского языка в современном мире Семейный очаг
Семейный очаг Александр Александрович Блок
Александр Александрович Блок О внедрении системы электронного общения с родителями 10 а класса МОУ СОШ №17 классного руководителя Печкуровой Е.А
О внедрении системы электронного общения с родителями 10 а класса МОУ СОШ №17 классного руководителя Печкуровой Е.А Мотивация и стимулирование труда персонала в государственном учреждении КГБОУ Барнаульская общеобразовательная школа-интернат №3
Мотивация и стимулирование труда персонала в государственном учреждении КГБОУ Барнаульская общеобразовательная школа-интернат №3 Проектирование технологического процесса на изготовление детали чашка каретки левая с годовой программой выпуска 40000 штук
Проектирование технологического процесса на изготовление детали чашка каретки левая с годовой программой выпуска 40000 штук Портреты великих исполнителей
Портреты великих исполнителей