Содержание
- 2. Введение Около 20 лет исследуются так называемые гибридные динамические системы, в которых присутствуют как континуальная так
- 3. Введение Системы, которые в отличие от гибридных систем обладают более сложно устроенными состояниями чем таблица состояний
- 4. Системы, основанные на знаниях Известны: множество высказываний о значениях лингвистических или логических переменных; экспертные или эмпирические
- 5. Системы, основанные на знаниях Не известны: точные описания состояний; точное описание динамики системы.
- 6. ПРИМЕРЫ 12 мая температура воды 14 градусов 12 мая течение слабое Направление течения: северо-западное Соленость воды:
- 7. ПРИМЕРЫ Правило 1. УСЛОВИЕ температура воды высокая, солёность низкая или средняя СПИСОК ДОБАВЛЯЕМЫХ ФАКТОВ зоопланктон размножается
- 8. ПРИМЕРЫ Правило 2. УСЛОВИЕ зоопланктон размножается, течение слабое СПИСОК ДОБАВЛЯЕМЫХ ФАКТОВ рост биомассы популяции, биомасса популяции
- 9. ПРИМЕРЫ Правило 3.(ВЫБОР ЦЕЛИ) УСЛОВИЕ направление линии визирования = неизвестно СПИСОК ДОБАВЛЯЕМЫХ ФАКТОВ цель: = поиск
- 10. ПРИМЕРЫ Правило 4.(ВЫБОР ЦЕЛИ) УСЛОВИЕ угол (АL,V)≥α, резерв времени СПИСОК ДОБАВЛЯЕМЫХ ФАКТОВ цель: = зависание СПИСОК
- 11. ПРИМЕРЫ Правило 5. (ВЫЧИСЛЕНИЕ ВЕКТОРА И МОМЕНТА СИЛЫ) УСЛОВИЕ цель = сближение, дистанция = D, вектор
- 12. ПРИМЕРЫ Правило 6.(ВЫБОР КОМБИНАЦИИ ВКЛЮЧАЕМЫХ ДВИГАТЕЛЕЙ) УСЛОВИЕ nтакта= четный, |F|≠0, угол (F,F(Cn))≤εα , |F|- |F(Cn)| СПИСОК
- 13. ПРИМЕРЫ Правило 7.(ВЫБОР КОМБИНАЦИИ ВКЛЮЧАЕМЫХ ДВИГАТЕЛЕЙ) УСЛОВИЕ nтакта= нечетный, |M|≠0, угол (M,M(Cn))≤ε ρ , |M|- |M(Cn)|
- 14. ПРАВИЛА Правило: П = , C, A и D - множества атомарных формул языка L -
- 15. C – условие правила, A – множество формул, таких, что соответствующие им факты добавляются в состояние
- 16. ПРАВИЛА Два класса правил Rτ и Rσ. С правилом класса Rτ связывается некоторое действие, производимое исполнительным
- 17. Динамические системы, основанные на правилах Применение правил как средства описания состояний и динамики приводит к динамическим
- 18. Рабочая память Совокупность таблиц или конечных отношений (таких, как, например, в реляционных базах данных), количество которых
- 19. Рабочая память Выполнимость и применимость: а) условие правила выполнено в текущем состоянии рабочей памяти тогда и
- 20. Стратегия управления 1 Выбирает некоторое правило из множества правил, проверяет выполнимость его условия в текущем состоянии
- 21. Стратегия управления 1 Если множество правил упорядочено, например, в алфавитном порядке (по первой букве, затем по
- 22. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ОСНОВАННЫЕ НА ПРАВИЛАХ Обозначим описанный процесс через К и положим K(x, Пσ )= φ(x)
- 23. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ОСНОВАННЫЕ НА ПРАВИЛАХ Осталось ввести время: для этого в языке выделим сорт переменной t,
- 24. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ОСНОВАННЫЕ НА ПРАВИЛАХ H = - динамическая система, основанная на правилах, где Φ: 2х
- 25. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ОСНОВАННЫЕ НА ПРАВИЛАХ Состояние системы - неподвижная точка уравнения Φ(χ) = χ Предельное состояние
- 26. ДИНАМИЧЕСКАЯ СИСТЕМА С ЦЕЛЕНАПРАВЛЕНЫМ ПОВЕДЕНИЕМ Задано некоторое Ω ⊆ 2х с определенным на нем нетранзитивным, асимметричным
- 27. ДИНАМИЧЕСКАЯ СИСТЕМА С ЦЕЛЕНАПРАВЛЕННЫМ ПОВЕДЕНИЕМ Пусть ω ∈ Ω Процедура π: 2х × 2х → МНОЖЕСТВО
- 28. ДИНАМИЧЕСКАЯ СИСТЕМА С ЦЕЛЕНАПРАВЛЕННЫМ ПОВЕДЕНИЕМ Стратегия управления 2. 1. Выбирается цель ω из множества Ω -
- 29. ПРИМЕР поведение обезьяны: «СОПЕРНИК-БАНАН-СОПЕРНИК», поведение активного корабля: «СТЫКОВКА- ОБЛЕТ- СТЫКОВКА».
- 30. ДИНАМИЧЕСКАЯ СИСТЕМА С ЦЕЛЕНАПРАВЛЕННЫМ ПОВЕДЕНИЕМ Получены результаты: об устойчивости таких систем и их управляемости (в смысле
- 31. Классификация динамических систем, основанных на правилах. Система H1: П= , P(t, y) – добавляемый факт; Система
- 32. Классификация динамических систем, основанных на правилах. S0 – начальное состояние систем H2 и H3. Система H21:
- 33. ПРЕДЕЛЬНЫЕ СОСТОЯНИЯ Р – объединение фактов, добавляемых всеми правилами; Ф – объединение фактов, удаляемых всеми правилами;
- 34. ПРЕДЕЛЬНЫЕ СОСТОЯНИЯ Система Н1: S0 ∪ Р; Системы Н21, Н31 : (S0 / Ф) ∪ Р;
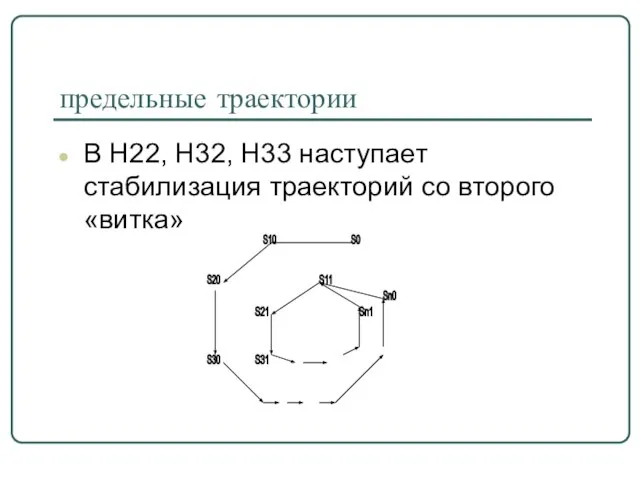
- 35. предельные траектории В Н22, Н32, Н33 наступает стабилизация траекторий со второго «витка»
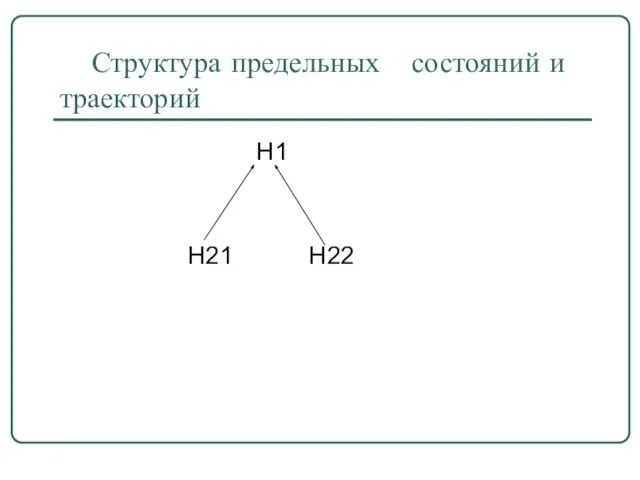
- 36. Структура предельных состояний и траекторий Н1 Н21 Н22
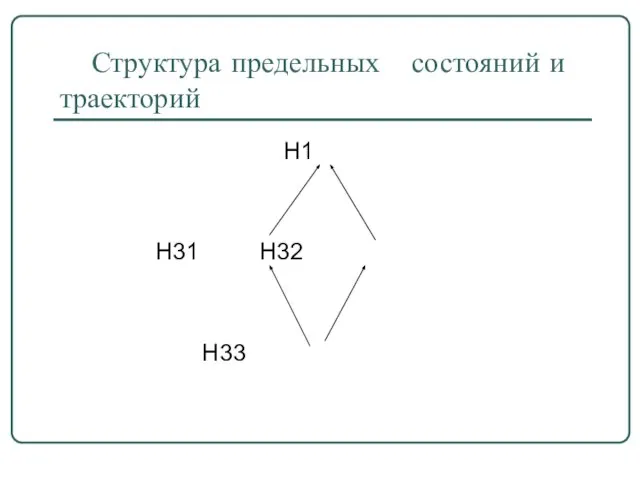
- 37. Структура предельных состояний и траекторий Н1 Н31 Н32 Н33
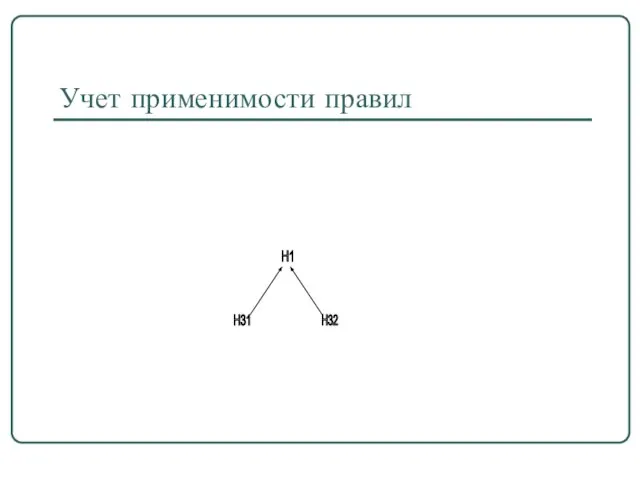
- 38. Учет применимости правил
- 39. СВОДКА РЕЗУЛЬТАТОВ Устойчивость и управляемость. Пусть I - некоторое возмущение в состоянии Si, т.е. i=Si{I}и имеет
- 40. СВОДКА РЕЗУЛЬТАТОВ Определение 3. Если X - множество состояний модели, то пара точек (x0,x1) в XґX
- 41. СВОДКА РЕЗУЛЬТАТОВ Существование плана и достижимость Определение 7. Планом достижения состояния ω из состояния ι будем
- 42. СВОДКА РЕЗУЛЬТАТОВ Теорема 5. Следующая процедура есть процедура планирования: 1.Пусть S есть целевое состояние, Mi текущее
- 43. Сводка результатов Теорема 6. Для всякой пары точек (x0 ,x1) ∈ XхX план П = П
- 44. ПУБЛИКАЦИИ ПО ТЕМЕ Gennady Osipov. Developing Models of a World with Regard for its Dynamics -
- 45. Публикации по теме Osipov G. Sazonova L., Intelligent system for fish stock prediction and allowable catch
- 46. ПУБЛИКАЦИИ ПО ТЕМЕ Осипов Г.С. Дискретные динамические модели, основанные на знаниях: архитектура, планирование, управляемость. Труды 4-го
- 47. Публикации по теме Бурдаев М.Н., Осипов Г.С., Хачумов В.М. О системе управления относительным движением космических аппаратов
- 48. ПУБЛИКАЦИИ ПО ТЕМЕ Г.С.Осипов. Интеллектуальные динамические системы и целенаправленное поведение. Научно - теоретический журнал «Искусственный интеллект»,
- 50. Скачать презентацию











































 НазванияХимическихЭлементов
НазванияХимическихЭлементов Акты применения права. Характеристика и классификация
Акты применения права. Характеристика и классификация САМЫЕ-САМЫЕ
САМЫЕ-САМЫЕ Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году
Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году Невидимые нити (2 класс)
Невидимые нити (2 класс) НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ
НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ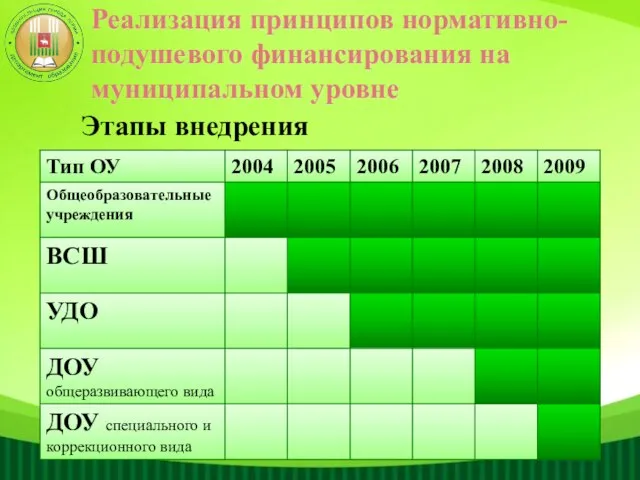 Реализация принципов нормативно-подушевого финансирования на муниципальном уровне
Реализация принципов нормативно-подушевого финансирования на муниципальном уровне Верейская по деньгам - ИТОГ
Верейская по деньгам - ИТОГ Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер
Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер Симметрия в архитектуре
Симметрия в архитектуре Презентация на тему Основные типы задач на проценты
Презентация на тему Основные типы задач на проценты  Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ
Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ Шаблон. Название темы
Шаблон. Название темы Презентация на тему Деревья
Презентация на тему Деревья  Учимся рисовать синичку (1)
Учимся рисовать синичку (1) Ох, уж эта функция
Ох, уж эта функция ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ
ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ Основы программирования промышленных роботов
Основы программирования промышленных роботов Образ матери в искусстве
Образ матери в искусстве Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы
Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы Шар ( сфера )
Шар ( сфера ) Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2
Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2 С Новым годом поздравляю
С Новым годом поздравляю Презентация на тему Книжная миниатюра Востока
Презентация на тему Книжная миниатюра Востока  О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ»
О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ» Начало Второй Мировой Войны
Начало Второй Мировой Войны Понятие психологии
Понятие психологии Страховые фонды Понятие, сущность, основные формы
Страховые фонды Понятие, сущность, основные формы