Линии одним росчерком пера

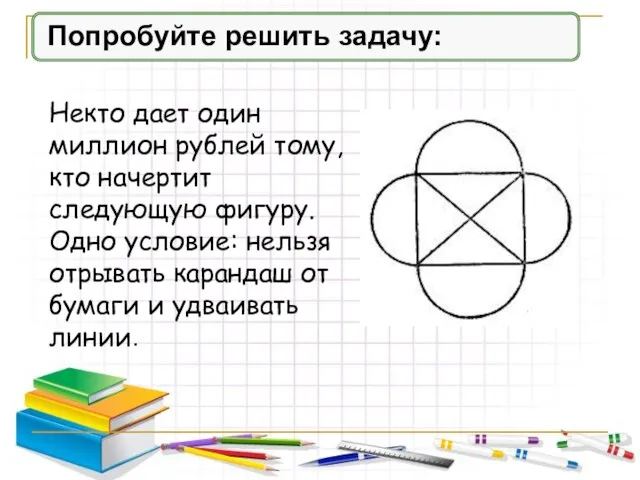
Попробуйте решить задачу:
Некто дает один миллион рублей тому, кто начертит следующую фигуру. Одно условие: нельзя отрывать карандаш от бумаги и удваивать линии.

Кёнигсбергские мосты
Вот перевод латинского текста, который взят из письма Эйлера к итальянскому математику и инженеру Маринони, отправленного из Петербурга 13 марта 1736 года:
"Некогда мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство... После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может".

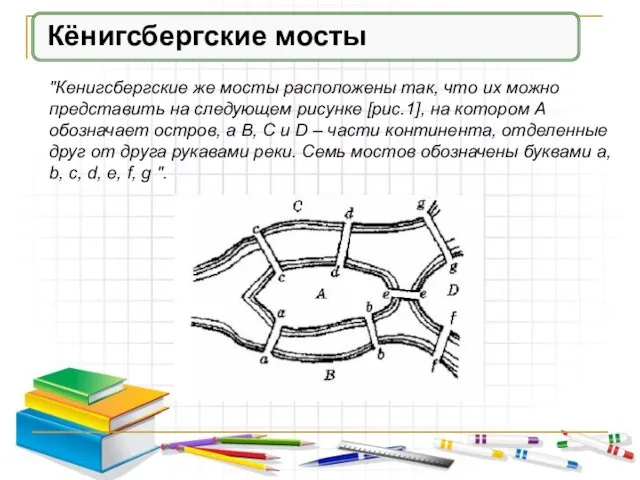
Кёнигсбергские мосты
"Кенигсбергские же мосты расположены так, что их можно представить на следующем рисунке [рис.1], на котором A обозначает остров, а B, C и D – части континента, отделенные друг от друга рукавами реки. Семь мостов обозначены буквами a, b, c, d, e, f, g ".

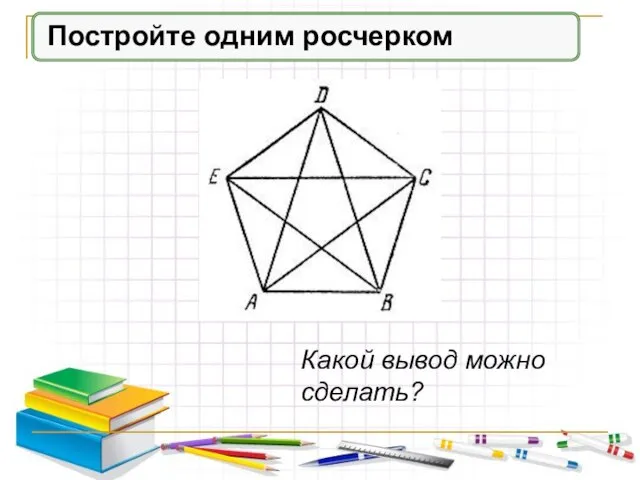
Постройте одним росчерком
Какой вывод можно сделать?

Иллюстрации Тая Уилсона

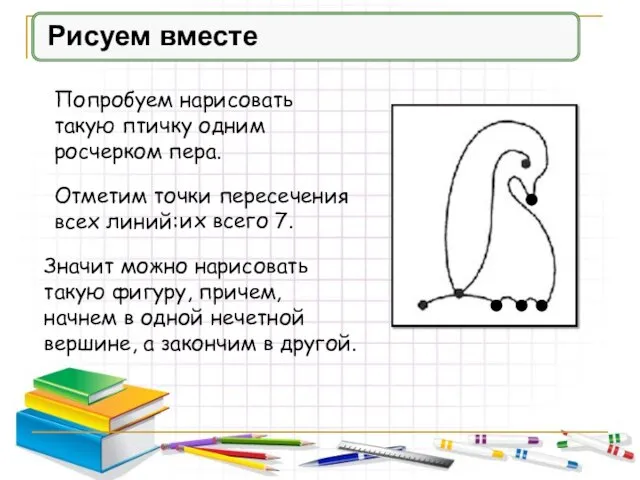
Рисуем вместе
Попробуем нарисовать такую птичку одним росчерком пера.
Отметим точки пересечения всех линий:
их всего 7.
Значит можно нарисовать такую фигуру, причем, начнем в одной нечетной вершине, а закончим в другой.