Содержание
- 9. «Величие человека в его способности мыслить.» Б.Паскаль.
- 10. Схема: Если А(условие), то Б(заключение). Пример: Если углы вертикальные, то они равны.
- 11. 1) В равностороннем треугольнике все углы равны. 2) Треугольник равнобедренный, если два его угла равны. 3)
- 12. Прямая теорема: Если А, то В. Обратная теорема: Если В, то А.
- 13. 1) Вертикальные углы равны. 2) В любом равностороннем треугольнике все углы равны. 3) Любой равносторонний треугольник
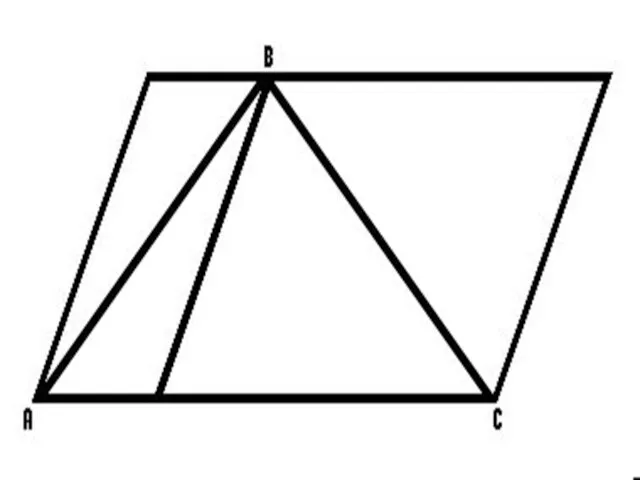
- 14. Вертикальные углы равны. Доказать: 1= 3 Доказательство: 1 4 2 3 значит,
- 15. Метод от противного 1) Делаем предположение, противоре- чащее тому, что требуется доказать. 2) Выясняем, что получается
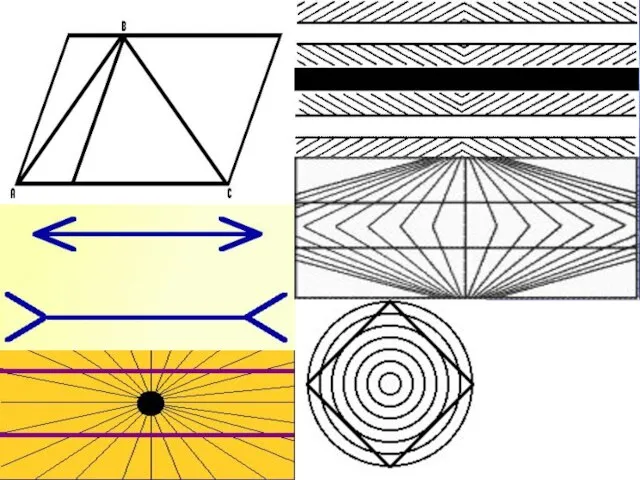
- 16. Исследуем, рассуждаем, доказываем…
- 17. Докажите методом от противного, что если углы не равны, то они не вертикальные.
- 18. Докажите методом от противного, что два смежных угла не могут быть оба тупыми.
- 19. Докажите методом от противного, что если в школе 500 учеников, то хотя бы у двух учеников
- 20. Докажите методом от противного, что во всяком треугольнике против бóльшего угла лежит бóльшая сторона.
- 21. Докажите методом от противного, что если при пересечении двух прямых секущей накрест лежащие углы равны, то
- 22. Математический софизм
- 23. Докажем, что 2 · 2 = 5 4 : 4 = 5 : 5 4( 1
- 24. Докажем, что 2=1.
- 25. Докажем, что 5 = 6 35 + 10 – 45 = 42 + 12 – 54
- 27. Скачать презентацию
















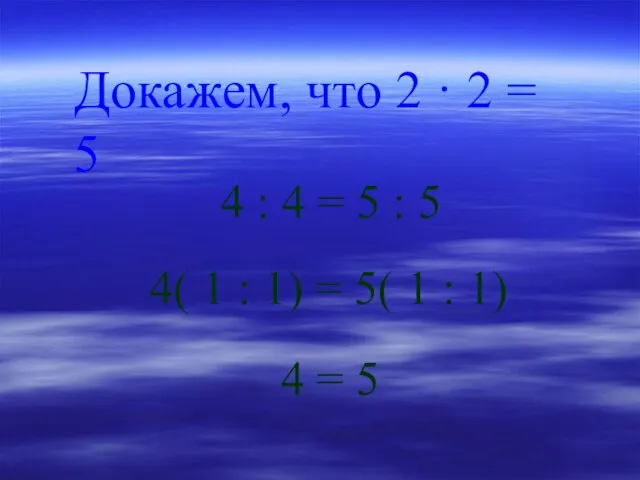
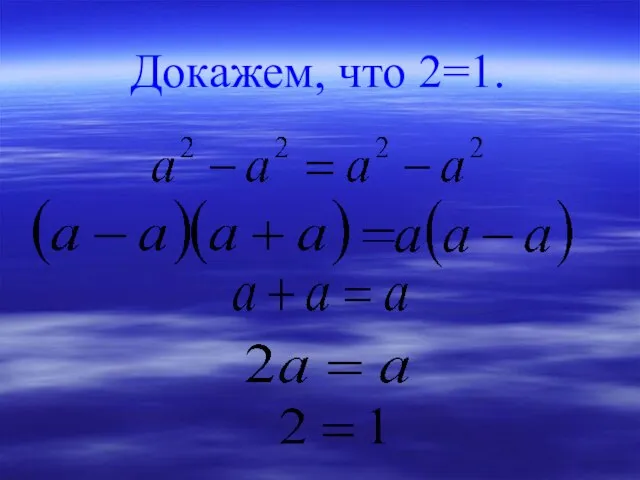

 Этика делового общения
Этика делового общения Информационная технология хранения данных
Информационная технология хранения данных Центр AFT представляет
Центр AFT представляет Решения компании «Электронные архивы Украины»
Решения компании «Электронные архивы Украины» В.В. Растрелли
В.В. Растрелли Все согласны
Все согласны Политическая система общества
Политическая система общества Осторожно: ядовитые растения
Осторожно: ядовитые растения dog breeds
dog breeds Фракталы))
Фракталы)) Мототакси. Особенности и преимущества
Мототакси. Особенности и преимущества занятие6 Азалия
занятие6 Азалия Геннадий Михасенко «Кандаурские мальчишки»
Геннадий Михасенко «Кандаурские мальчишки» Презентация на тему Антарктида, история открытия и исследования
Презентация на тему Антарктида, история открытия и исследования Пушкин в Лицее
Пушкин в Лицее СОЛСТИК РЕВАЙВ Solstic Revive
СОЛСТИК РЕВАЙВ Solstic Revive  МЕЖДУНАРОДНЫЙ ЖУРНАЛ О МОБИЛЬНОЙ ТЕХНИКЕ
МЕЖДУНАРОДНЫЙ ЖУРНАЛ О МОБИЛЬНОЙ ТЕХНИКЕ Районное методическое объединение классных руководителей Нормативно-законодательная база ученического самоуправления
Районное методическое объединение классных руководителей Нормативно-законодательная база ученического самоуправления kochetkova
kochetkova Пятно как средство выражения. Композиция, как ритм пятна
Пятно как средство выражения. Композиция, как ритм пятна Метан и его свойства
Метан и его свойства Презентация на тему Защита окружающей среды
Презентация на тему Защита окружающей среды Презентация на тему История государственных символов России
Презентация на тему История государственных символов России Тепловизор
Тепловизор Положительные и отрицательные числа
Положительные и отрицательные числа Chopaev Islam 8(3) Класс
Chopaev Islam 8(3) Класс Рекомендации по заполнению технологической карты межведомственного взаимодействия (ТКМВ)
Рекомендации по заполнению технологической карты межведомственного взаимодействия (ТКМВ) Movie Quiz
Movie Quiz