Содержание
- 2. Знакомство Для общения с компьютерами создано множество специальных компьютерных языков. Они называются языками программирования. Американские ученые,
- 3. Понятие исполнителя Исполнитель – физический или виртуальный объект, производящий выполнение алгоритма. Примеры: 1. Черепашка - перемещается
- 4. Исполнитель Черепашка – исполнитель среды ЛогоМиры. Черепашкой можно управлять, задавая ей команды: Перемещать; Поворачивать; Изменять её
- 5. Команды
- 6. Аннотация На слайде 7 предлагается поэтапное построение результата программы на языке ЛогоМиры исполнителем Черепашка . Каждый
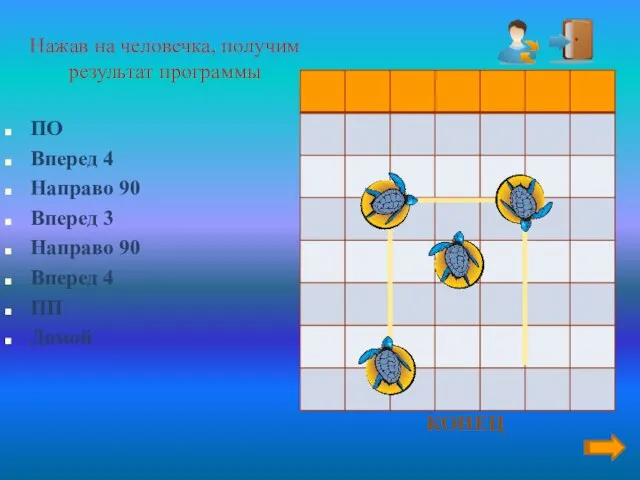
- 7. Нажав на человечка, получим результат программы ПО Вперед 4 Направо 90 Вперед 3 Направо 90 Вперед
- 8. Программа Начало Команды программы Конец программы Основные алгоритмические конструкции Исполнителя - Робота Тело программы Программа Начало
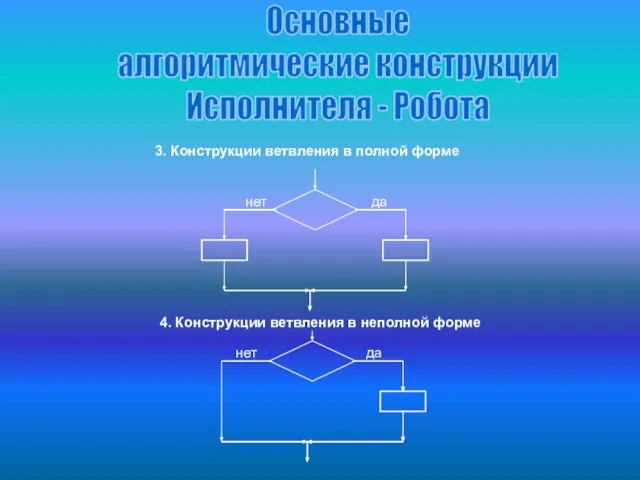
- 9. Основные алгоритмические конструкции Исполнителя - Робота 3. Конструкции ветвления в полной форме Если То Иначе Конец
- 10. Основные алгоритмические конструкции Исполнителя - Робота 3. Конструкции ветвления в полной форме 4. Конструкции ветвления в
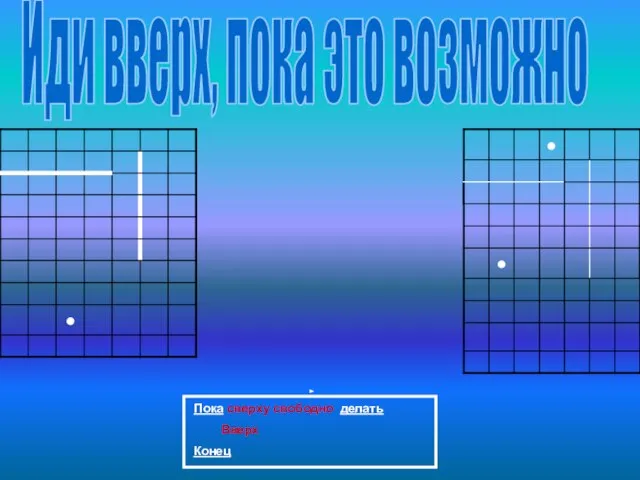
- 11. Иди вверх, пока это возможно Пока сверху свободно делать Вверх Конец
- 12. Основные алгоритмические конструкции Исполнителя - Робота Тело цикла 6. Пока делать Конец 5. Повторить … раз
- 13. Простые и составные условия. Работа Исполнителя - Робота в условиях полной неопределенности
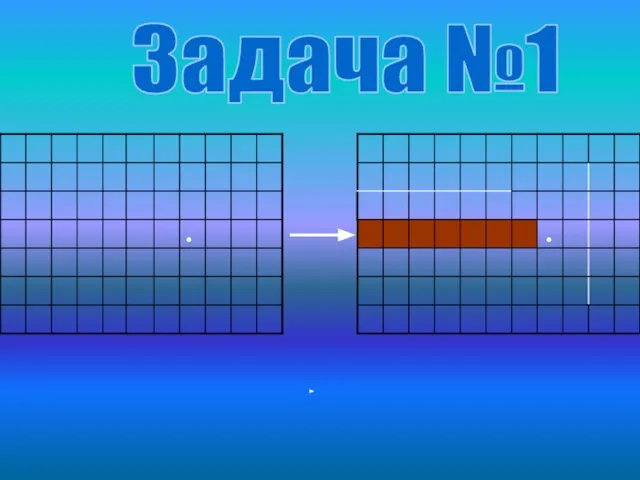
- 14. Задача №1
- 15. Задача №2
- 16. Составные условия Логические операции: 1. И (конъюнкция) 2. ИЛИ (дизъюнкция) 3. НЕ (отрицание) Если Сверху свободно
- 17. Движение по коридору
- 18. Повторяющиеся мотивы
- 20. Кто может быть исполнителем алгоритма? Исполнителем алгоритма может быть не только человек, но и автоматическое устройство
- 21. Разработка и исполнение Разрабатывает алгоритмы: человек, Исполняют алгоритмы: люди и устройства – компьютеры, роботы, станки, спутники,
- 22. Исполнителя характеризует: Системой команд Исполнителя называется совокупность всех команд, которые может выполнить Исполнитель. Совокупность всех действий,
- 23. Некоторые основные понятия теории графов Граф – рисунок, состоящий из множества точек и множества отрезков, оба
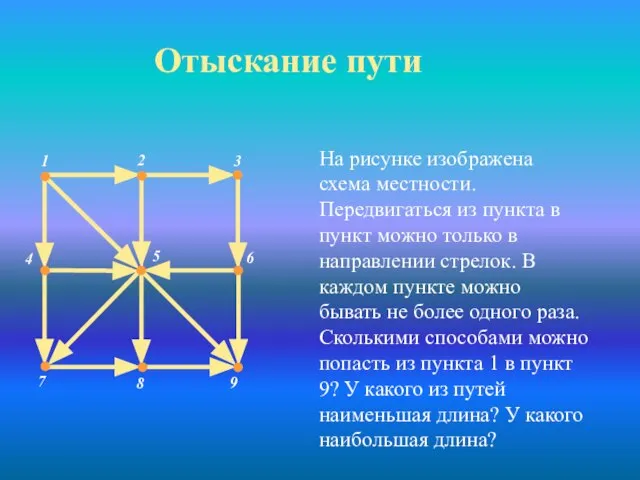
- 24. Отыскание пути На рисунке изображена схема местности. Передвигаться из пункта в пункт можно только в направлении
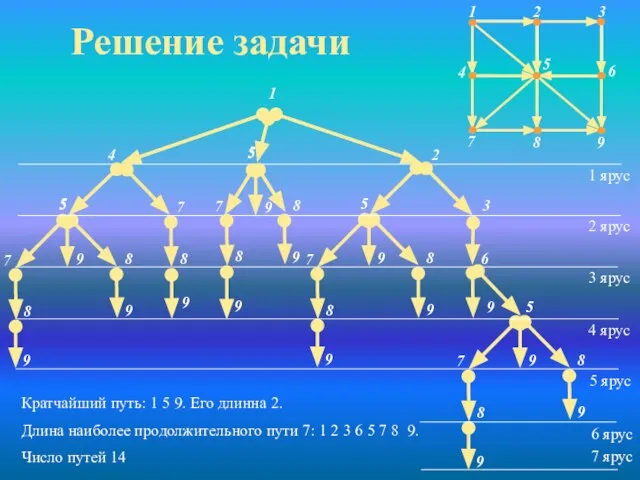
- 25. Решение задачи Кратчайший путь: 1 5 9. Его длинна 2. Длина наиболее продолжительного пути 7: 1
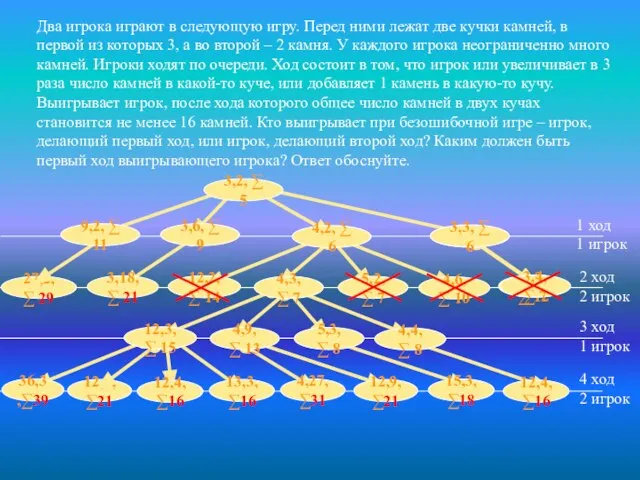
- 26. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых
- 27. Решение задачи Правильное указание выигрывающего игрока и его ходов со строгим доказательством правильности (с помощью дерева
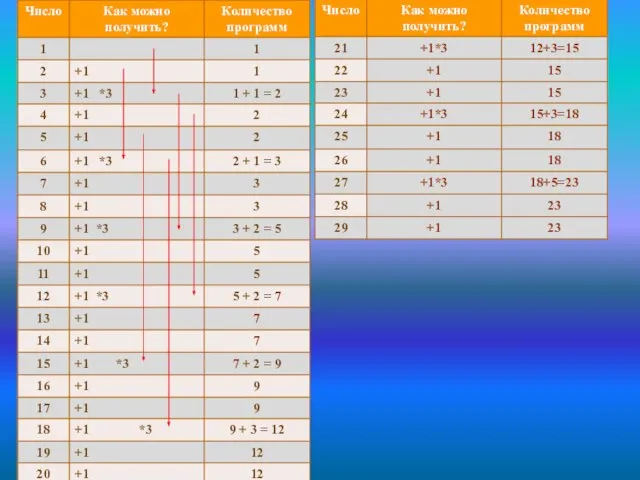
- 28. Ещё пример задачи У исполнителя Утроитель две команды, которым присвоены номера: 1. прибавь 1, 2. умножь
- 31. Скачать презентацию


















 Как животные готовятся к зиме
Как животные готовятся к зиме Wi-Fi роутер Xiaomi Mi Router 4C
Wi-Fi роутер Xiaomi Mi Router 4C БИТ. ФИНАНС - программный прродукт для автоматизации финансового и управленческого учета
БИТ. ФИНАНС - программный прродукт для автоматизации финансового и управленческого учета О внесении изменений в паспорт и перечень показателей федерального проекта Успех каждого ребенка и методику их расчета
О внесении изменений в паспорт и перечень показателей федерального проекта Успех каждого ребенка и методику их расчета Фундаментальные и прикладные вопросы нейробиологии
Фундаментальные и прикладные вопросы нейробиологии Богдан Xumikk Трибушной - профессиональный аналитик
Богдан Xumikk Трибушной - профессиональный аналитик КОМПЛЕКСНОЕ ОСНАЩЕНИЕ ПРЕДПРИЯТИЙ ОБЩЕСТВЕННОГО ПИТАНИЯ
КОМПЛЕКСНОЕ ОСНАЩЕНИЕ ПРЕДПРИЯТИЙ ОБЩЕСТВЕННОГО ПИТАНИЯ Тема №21. Принцип разделения власти
Тема №21. Принцип разделения власти Субкультуры и контркультуры
Субкультуры и контркультуры Сущность денег. Эмиссия денег
Сущность денег. Эмиссия денег Рынок Транспортной тары. Текущая ситуация и тенденции развития.
Рынок Транспортной тары. Текущая ситуация и тенденции развития. Юзабилити интернет-магазинов: Что не видят продавцы и покупатели
Юзабилити интернет-магазинов: Что не видят продавцы и покупатели Политика и власть. Тест по обществознанию
Политика и власть. Тест по обществознанию Развитие науки XVI - XVIII вв
Развитие науки XVI - XVIII вв Подросток и Закон
Подросток и Закон Исследовательская работа «Земля и луна»
Исследовательская работа «Земля и луна» Основы дизайн-проектирования. Художественное оформление книги. 2 класс
Основы дизайн-проектирования. Художественное оформление книги. 2 класс My World of Music
My World of Music Современные подходы к целеполаганию
Современные подходы к целеполаганию Пейзаж родной природы
Пейзаж родной природы Презентация на тему Туберкулез, туберкулез легких
Презентация на тему Туберкулез, туберкулез легких  Демон. Трактовка Лермонтова и Врубеля
Демон. Трактовка Лермонтова и Врубеля Презентация на тему Многообразие водорослей их роль в природе практическое значение
Презентация на тему Многообразие водорослей их роль в природе практическое значение  Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Мониторинг СМИ Украины
Мониторинг СМИ Украины Как праздновали Новый Год и Рождество в Самаре в начале прошлого века
Как праздновали Новый Год и Рождество в Самаре в начале прошлого века Лыжный спорт
Лыжный спорт Поведение и здоровье
Поведение и здоровье