Исследование физических моделей

Построение и исследование модели на примере движения тела, брошенного под углом к горизонту.
Содержательная постановка задачи:
-в процессе тренировки теннисистов используют автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.

Качественная описательная модель
Из условия задачи можно сформулировать основные предположения:
-мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
-изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g=9,8 м/с2 и движение по оси OY можно считать равноускоренным;
-скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси OX можно считать равномерным

Формальная модель
Для формализации модели используем формулы равномерного и равноускоренного движения.
При заданных начальной скорости v0 и угле бросания α значения координат дальности полета х и высоты у от времени можно описать следующими формулами:
Высоту мячика L над землей на расстоянии s определяем по формуле:
Попадание произойдет, если значение высоты L мячика будет удовлетворять неравенству:

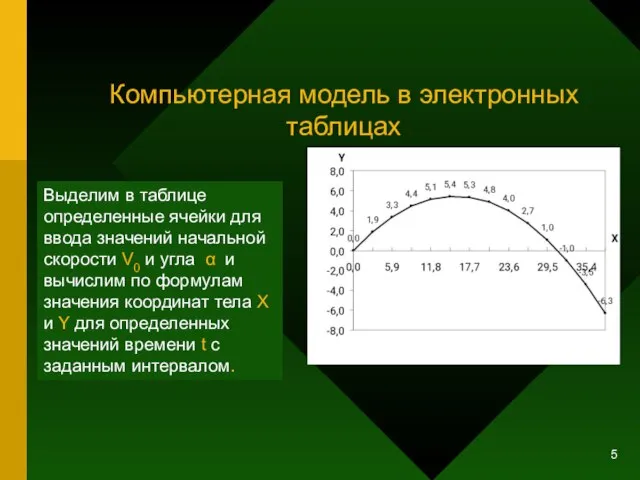
Компьютерная модель в электронных таблицах
Выделим в таблице определенные ячейки для ввода значений начальной скорости V0 и угла α и вычислим по формулам значения координат тела Х и Y для определенных значений времени t с заданным интервалом.

Исследование модели
Исследуем модель и определим с заданной точностью 0,1º диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/с.
Воспользуемся для этого методом Подбор параметров.
Выводы: Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений угла бросания ( указать ! ) , который обеспечивает попадание в мишень высотой 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.

Биологические модели развития популяций

В биологии при исследовании развития развития биосистем строятся динамические модели изменения численности популяций различных живых существ с учетом различных факторов.
Взаимовлияние популяций рассматривается в моделях типа «хищник – жертва».
Формальная модель
Динамику численности популяций исследуют на модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент:
а- коэффициент роста

В модели ограниченного роста учитывается коэффициент перенаселенности, связанный с нехваткой питания, болезнями и т.д., который замедляет рост популяции с увеличением ее численности:
b – коэффициент перенаселенности (b < a):

В модели ограниченного роста с отловом учитывается, что на численность популяции промысловых животных и рыб оказывает влияние величина ежегодного
отлова – с:
В модели «хищник – жертва» количество жертв xn и количество хищников уn связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками:

Компьютерная модель
Построим в электронных таблицах компьютерную модель, позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста, ограниченного роста, ограниченного роста с отловом и «хищник – жертва».
A, b, c, f – значения коэффициентов, влияющих на изменение численности жертв
D, e - значения коэффициентов, влияющих на изменение численности хищников
Столбец D-численность популяции по модели неограниченного роста;
Столбец Е-численность популяции по модели ограниченного роста;
Столбец F- ограниченного роста c отловом;
Столбцы G и H -численность популяции по модели «хищник – жертва»

Исследование модели
Провести исследование моделей роста популяций различного типа, задавая различные значения коэффициентов и начальные численности популяций. Подобрать значения коэффициентов, чтобы:
- определить через сколько лет произойдет удвоение численности популяции в модели неограниченного роста;
численность популяций в моделях ограниченного роста и ограниченного роста с отловом стабилизировалась примерно на одном уровне (так определяют квоты на ловлю рыбы);
в модели «жертва – хищник» численность жертв и хищников стабилизировалась со временем (так определяют охотничьи квоты)
и сделать выводы.

Геоинформационные модели

Геоинформационное моделирование базируется на создании многослойных электронных карт, в которых опорный слой описывает географию определенной территории, а каждый из остальных – один из аспектов состояния этой территории. На географическую карту могут быть выведены различные слои объектов: города, дороги, аэропорты и др.
См. Рабочий стол/Обучающие программы/Карта Кемерово

Интерактивные географические карты реализуются с использованием векторной графики и связаны с базами данных, которые хранят всю необходимую информацию об объектах, изображенных на картах.

Геоинформационные модели позволяют с помощью географических карт представлять статистическую информацию о различных регионах.

Задание:
С помощью геоинформационной модели «Численность населения в странах мира» (файл mapstats.xls) найдите свой регион (страну) и выпишите следующую информацию:

Оптимизационное моделирование в экономике

В сфере управления сложными системами применяется оптимизационное моделирование, в процессе которого осуществляется поиск наиболее оптимального пути развития системы.
Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.

Содержательная постановка проблемы
В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и Б тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.
Необходимо выбрать оптимальное сочетание способов раскроя, для того, чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.

Компьютерная модель
Искать решение задачи путем создания и исследования компьютерной модели в электронных таблицах Excel.
Исследование модели
Для поиска оптимального выбора значений параметров, который соответствует минимальному значению целевой функции используем надстройку электронных таблиц Поиск решения.
Модель «Оптимизационное моделирование» хранится в файле model.xls