Содержание
- 2. Графом называют множество, в котором некоторые пары элементов выделены; элементы каждой выделенной пары называют смежными друг
- 3. Любой многоугольник можно считать графом. У треугольника любые две вершины смежные, а у четырехугольника четыре пары
- 4. При изображении графа на плоскости неважно, каково обычное расстояние между вершинами и какой вид имеют ребра.
- 5. О путях и графах. Если дан граф, то двигаясь по его ребрам (как «по дорогам»), можно
- 6. Граф родственных отношений. Семья, в которой есть отец, мать, их сын и дочь, а также мать
- 7. С помощью графов можно составить генеалогическое древо своей семьи.
- 8. Задача о Кенигсбергских мостах. В городе Кенигсберге (ныне Калининград – самый западный областной центр России) есть
- 9. Задача о мостах превращается в такую задачу про этот граф: есть ли в графе путь, который
- 11. Скачать презентацию
Слайд 2Графом называют множество, в котором некоторые пары элементов выделены;
элементы каждой выделенной
Графом называют множество, в котором некоторые пары элементов выделены;
элементы каждой выделенной
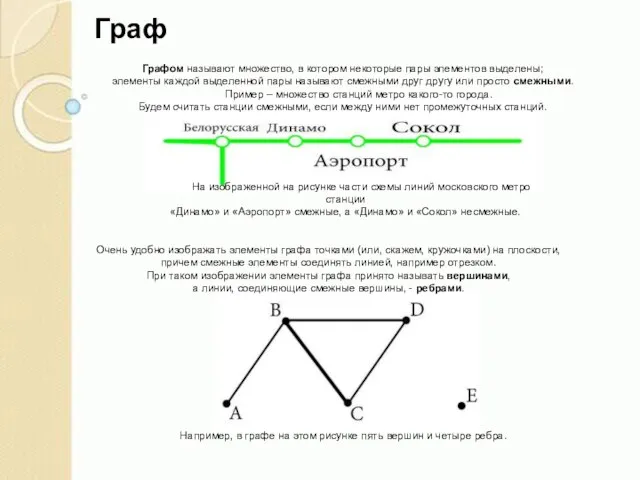
Пример – множество станций метро какого-то города.
Будем считать станции смежными, если между ними нет промежуточных станций.
На изображенной на рисунке части схемы линий московского метро станции
«Динамо» и «Аэропорт» смежные, а «Динамо» и «Сокол» несмежные.
Очень удобно изображать элементы графа точками (или, скажем, кружочками) на плоскости,
причем смежные элементы соединять линией, например отрезком.
При таком изображении элементы графа принято называть вершинами,
а линии, соединяющие смежные вершины, - ребрами.
Например, в графе на этом рисунке пять вершин и четыре ребра.
Граф
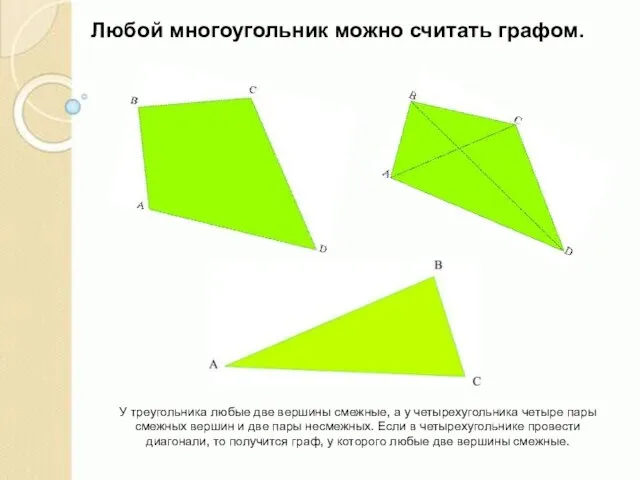
Слайд 3Любой многоугольник можно считать графом.
У треугольника любые две вершины смежные, а у
Любой многоугольник можно считать графом.
У треугольника любые две вершины смежные, а у
Слайд 4При изображении графа на плоскости неважно,
каково обычное расстояние между вершинами и
При изображении графа на плоскости неважно, каково обычное расстояние между вершинами и
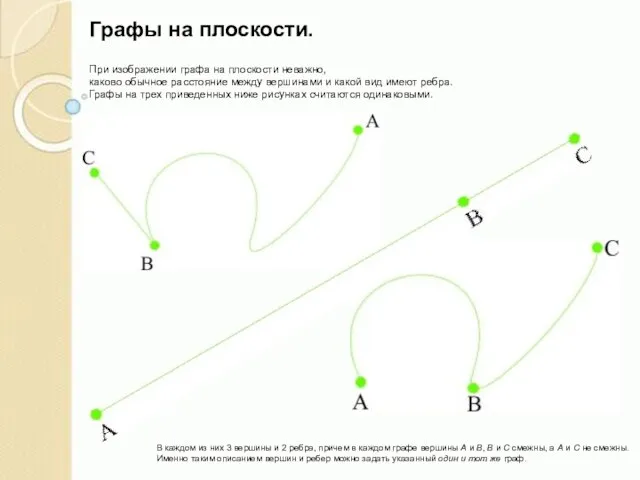
Графы на плоскости.
В каждом из них 3 вершины и 2 ребра, причем в каждом графе вершины А и В, В и С смежны, а А и С не смежны.
Именно таким описанием вершин и ребер можно задать указанный один и тот же граф.
Слайд 5О путях и графах.
Если дан граф, то двигаясь по его ребрам (как
О путях и графах.
Если дан граф, то двигаясь по его ребрам (как
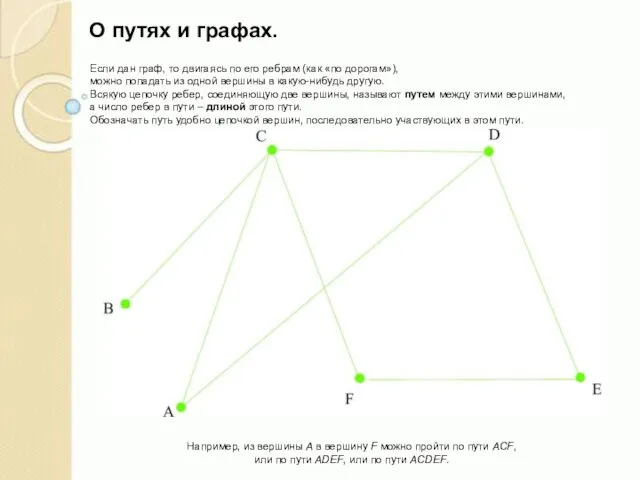
можно попадать из одной вершины в какую-нибудь другую.
Всякую цепочку ребер, соединяющую две вершины, называют путем между этими вершинами,
а число ребер в пути – длиной этого пути.
Обозначать путь удобно цепочкой вершин, последовательно участвующих в этом пути.
Например, из вершины А в вершину F можно пройти по пути ACF,
или по пути ADEF, или по пути ACDEF.
Слайд 6Граф родственных отношений.
Семья, в которой есть отец, мать, их сын и дочь,
Граф родственных отношений.
Семья, в которой есть отец, мать, их сын и дочь,
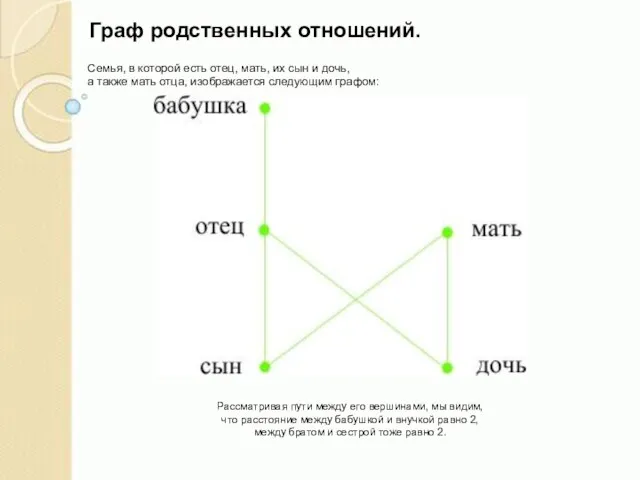
а также мать отца, изображается следующим графом:
Рассматривая пути между его вершинами, мы видим,
что расстояние между бабушкой и внучкой равно 2,
между братом и сестрой тоже равно 2.
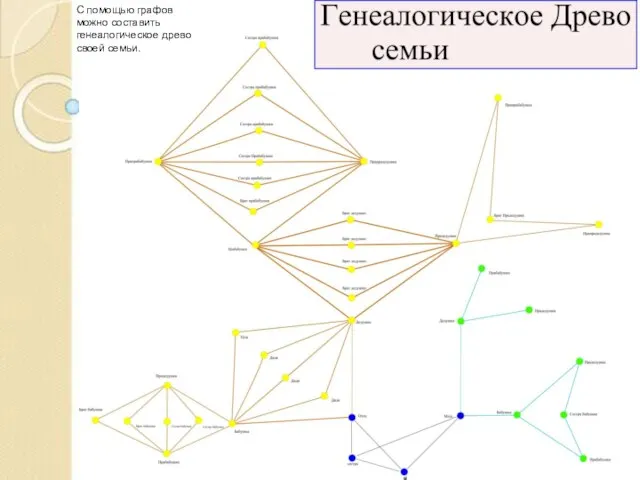
Слайд 7С помощью графов
можно составить
генеалогическое древо
своей семьи.
С помощью графов
можно составить
генеалогическое древо
своей семьи.
Слайд 8Задача о Кенигсбергских мостах.
В городе Кенигсберге (ныне Калининград – самый западный
Задача о Кенигсбергских мостах.
В городе Кенигсберге (ныне Калининград – самый западный
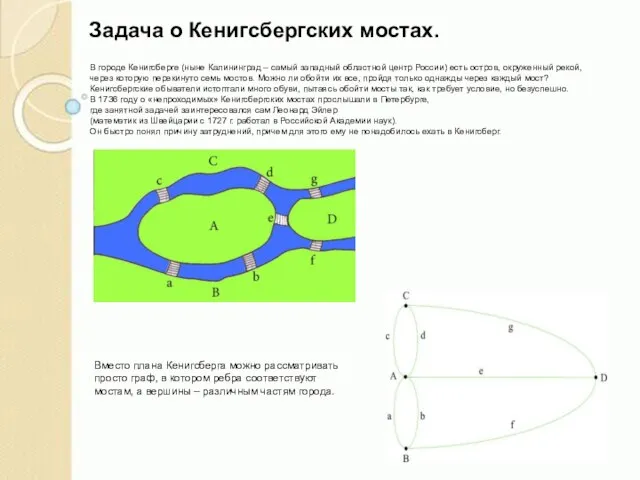
через которую перекинуто семь мостов. Можно ли обойти их все, пройдя только однажды через каждый мост?
Кенигсбергские обыватели истоптали много обуви, пытаясь обойти мосты так, как требует условие, но безуспешно.
В 1736 году о «непроходимых» Кенигсбергских мостах прослышали в Петербурге,
где занятной задачей заинтересовался сам Леонард Эйлер
(математик из Швейцарии с 1727 г. работал в Российской Академии наук).
Он быстро понял причину затруднений, причем для этого ему не понадобилось ехать в Кенигсберг.
Вместо плана Кенигсберга можно рассматривать просто граф, в котором ребра соответствуют мостам, а вершины – различным частям города.
Слайд 9Задача о мостах превращается в такую задачу про этот граф: есть ли
Задача о мостах превращается в такую задачу про этот граф: есть ли

который проходит по разу через каждое ребро? Допустим, что, идя по такому пути,
мы зашли по какому-то ребру a в вершину А. Понятно, что выйти из А
придется по другому ребру (скажем, b) – ведь проходить второй раз через ребро a не разрешается.
Итак, к вершине А ведут по крайней мере 2 ребра: a и b. Если, продолжая движение,
мы снова попадем в вершину А по еще одному ребру с,
то выйдем из А по опять-таки новому, «нехоженому» ребру d, т.е. возникнет еще одна пара ребер.
И так далее – ребра, сходящиеся в вершине А, разбиваются на такие пары:
Задача о Кенигсбергских мостах.
Итак, вывод: раз ребра, сходящиеся в вершине А, можно разбить на пары,
то таких ребер четное число.
Значит, если в каком-либо графе есть путь, который проходит ровно по одному разу
через каждое ребро, то в каждой вершине такого графа, кроме, может быть, двух,
должно сходиться четное число ребер.
 Методы и формы работы в программе дополнительного образования
Методы и формы работы в программе дополнительного образования Синдром одержимости
Синдром одержимости Лек 3 харак кулин продукции
Лек 3 харак кулин продукции Символизм и модерн как стилистические направления начала XX века
Символизм и модерн как стилистические направления начала XX века Бухгалтерская (финансовая) отчетность. Отчет об изменениях капитала. Лекция 5
Бухгалтерская (финансовая) отчетность. Отчет об изменениях капитала. Лекция 5 Поддержка стандарта OpenGIS в СУБД ЛИНТЕР
Поддержка стандарта OpenGIS в СУБД ЛИНТЕР № 1 Введение в дисциплину
№ 1 Введение в дисциплину Как сохранить здоровье ребенка? 7 класс
Как сохранить здоровье ребенка? 7 класс Warp Knitted Safety Jacket Fabric
Warp Knitted Safety Jacket Fabric Родительское собраниепо теме"Школа-дом-одна семья"
Родительское собраниепо теме"Школа-дом-одна семья" ТЕМА: ОБОРУДОВАНИЕ ДЛЯ ПРИЕМКИ ПРОДУКЦИИ
ТЕМА: ОБОРУДОВАНИЕ ДЛЯ ПРИЕМКИ ПРОДУКЦИИ Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов
Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов Тест по экономике
Тест по экономике МОУ Лицей №74
МОУ Лицей №74 Разработка модели управления Разработка модели управленияпроцессом полоролевого воспитания детей дошкольного и младшего шк
Разработка модели управления Разработка модели управленияпроцессом полоролевого воспитания детей дошкольного и младшего шк Проверочная работа по теме: «Функциональное устройство компьютера» (Запишите на листочках свои имя и фамилию,номер варианта и за
Проверочная работа по теме: «Функциональное устройство компьютера» (Запишите на листочках свои имя и фамилию,номер варианта и за Итоги проведения конкурсных процедур и приемки государственных контрактов, выполненных в рамках ФЦПРО на 2011-2015 годы в 2011 году
Итоги проведения конкурсных процедур и приемки государственных контрактов, выполненных в рамках ФЦПРО на 2011-2015 годы в 2011 году Способы разделения смесей
Способы разделения смесей Характерные черты информационного общества
Характерные черты информационного общества Школьная профилактически - образовательная программа «УРОКИ ЗДОРОВЬЯ»
Школьная профилактически - образовательная программа «УРОКИ ЗДОРОВЬЯ» Инклюзивное образование
Инклюзивное образование ВНИМАНИЕ!!!
ВНИМАНИЕ!!! Повторение изученного по фонетике и орфоэпии
Повторение изученного по фонетике и орфоэпии OKD_chistaya_linia
OKD_chistaya_linia Культура через призму психоанализа: Фрейд, Юнг, Фромм
Культура через призму психоанализа: Фрейд, Юнг, Фромм Поручение Президента РФ
Поручение Президента РФ Презентация на тему Money деньги
Презентация на тему Money деньги  Украинцы в Красноярском крае
Украинцы в Красноярском крае