Компьютерная модель радиоэлектронных средств (РЭС)

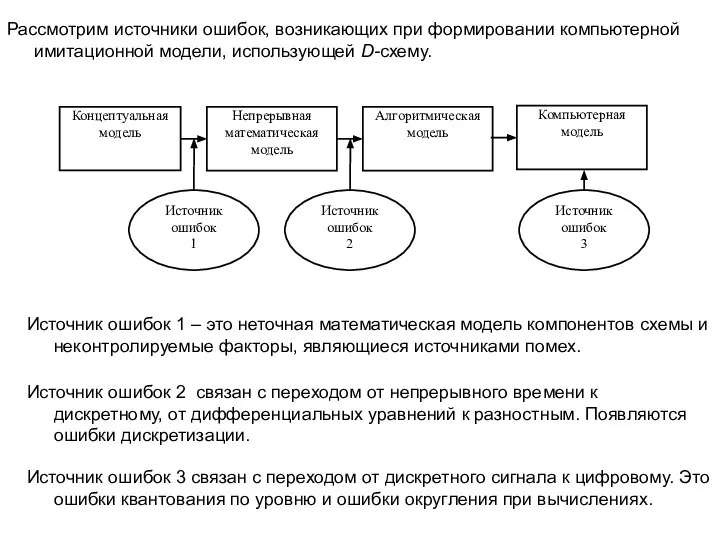
Рассмотрим источники ошибок, возникающих при формировании компьютерной имитационной модели, использующей D-схему.
Источник ошибок 1 – это неточная математическая модель компонентов схемы и неконтролируемые факторы, являющиеся источниками помех.
Источник ошибок 2 связан с переходом от непрерывного времени к дискретному, от дифференциальных уравнений к разностным. Появляются ошибки дискретизации.
Источник ошибок 3 связан с переходом от дискретного сигнала к цифровому. Это ошибки квантования по уровню и ошибки округления при вычислениях.

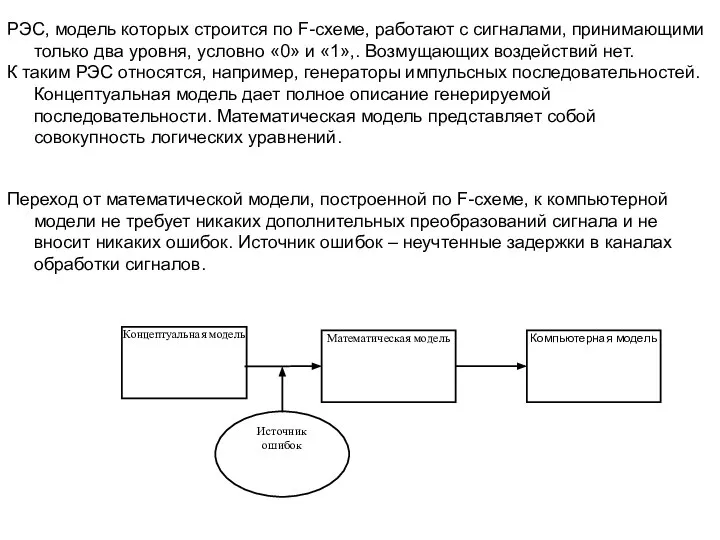
РЭС, модель которых строится по F-схеме, работают с сигналами, принимающими только два уровня, условно «0» и «1»,. Возмущающих воздействий нет.
К таким РЭС относятся, например, генераторы импульсных последовательностей. Концептуальная модель дает полное описание генерируемой последовательности. Математическая модель представляет собой совокупность логических уравнений.
Переход от математической модели, построенной по F-схеме, к компьютерной модели не требует никаких дополнительных преобразований сигнала и не вносит никаких ошибок. Источник ошибок – неучтенные задержки в каналах обработки сигналов.

Математическая модель РЭС по D-схеме
Математическая модель, построенная по D-схеме, в общем случае описывается нелинейным дифференциальным уравнением. Часто удается разделить нелинейное и линейное преобразования процессов и модель представляется в виде соединения безынерционных нелинейных элементов с функциональной связью выходных и входных процессов: y = f(x) и инерционных линейных элементов, описывающихся линейным дифференциальным уравнением
В инженерной практике обычно используют не дифференциальное уравнение, а другие связанные с ним формы математического описания.
Передаточная функция
Комплексная частотная характеристика

Переходная характеристика как реакция линейной системы на единичный скачок входного воздействия
Импульсная характеристика как реакция линейной системы на δ-функцию
Импульсная характеристика используется для расчета выходного процесса по формуле свертки.
Для переходного режима
для установившегося режима
Для перехода к компьютерной модели нужно от непрерывных сигналов перейти к дискретным. При этом можно использовать любую из форм описания РЭС.

1. Численное решение нелинейного дифференциального уравнения. Уравнение приводится к виду
Разложим решение уравнения y(t) в ряд Тейлора в окрестности точки при t = t0
и ограничимся двумя первыми членами разложения
Перепишем это выражение в форме, удобной для пошагового вычисления, обозначив t0 = tn, t = tn+1, y(t0) = yn, y(t) = yn+1, и учитывая, что
Это решение по прямому методу Эйлера. Оно получается на основе линейной экстраполяции с углом наклона прямой F(yn, xn, tn)

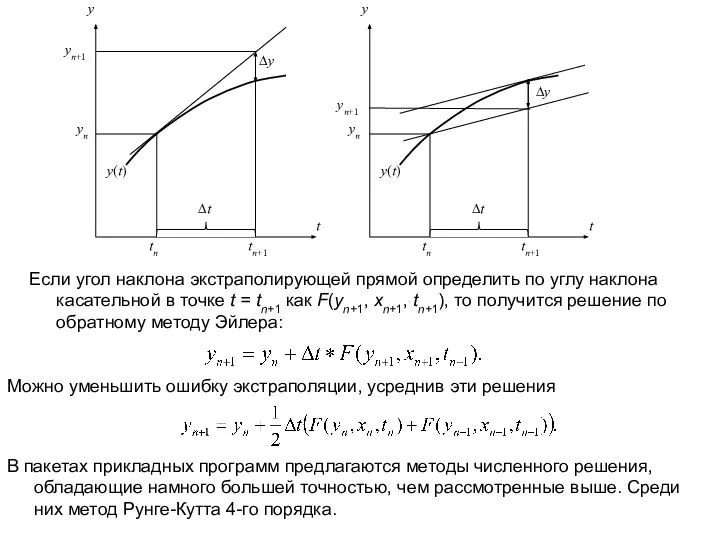
Если угол наклона экстраполирующей прямой определить по углу наклона касательной в точке t = tn+1 как F(yn+1, xn+1, tn+1), то получится решение по обратному методу Эйлера:
Можно уменьшить ошибку экстраполяции, усреднив эти решения
В пакетах прикладных программ предлагаются методы численного решения, обладающие намного большей точностью, чем рассмотренные выше. Среди них метод Рунге-Кутта 4-го порядка.

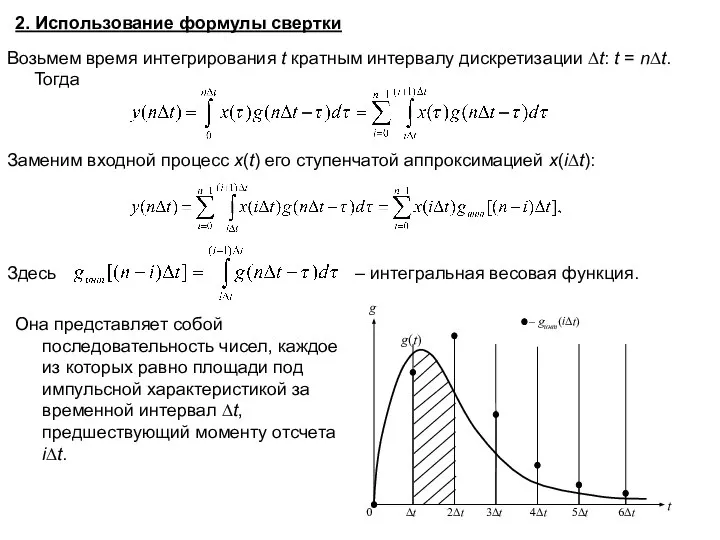
2. Использование формулы свертки
Возьмем время интегрирования t кратным интервалу дискретизации ∆t: t = n∆t. Тогда
Заменим входной процесс x(t) его ступенчатой аппроксимацией x(i∆t):
Здесь
– интегральная весовая функция.
Она представляет собой последовательность чисел, каждое из которых равно площади под импульсной характеристикой за временной интервал ∆t, предшествующий моменту отсчета i∆t.

При малом ∆t можно использовать ступенчатую аппроксимацию импульсной характеристики и криволинейную трапецию заменить прямоугольником. Тогда
и формула дискретной свертки
3. Замена непрерывной передаточной функции дискретной передаточной функцией
Первый путь – использование дискретного преобразования Лапласа (Z-преобразования
Непрерывная передаточная функция K(p) связана с импульсной характеристикой g(t) преобразованием Лапласа. Дискретизацией импульсной характеристики получается весовая функция g[n]. Z-преобразование от весовой функции даст дискретную передаточную характеристику K(z).

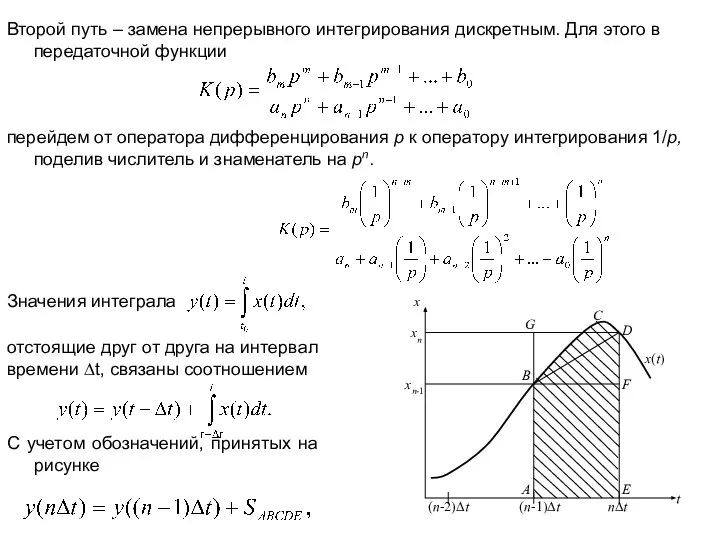
Второй путь – замена непрерывного интегрирования дискретным. Для этого в передаточной функции
перейдем от оператора дифференцирования p к оператору интегрирования 1/p, поделив числитель и знаменатель на pn.
Значения интеграла
отстоящие друг от друга на интервал
времени ∆t, связаны соотношением
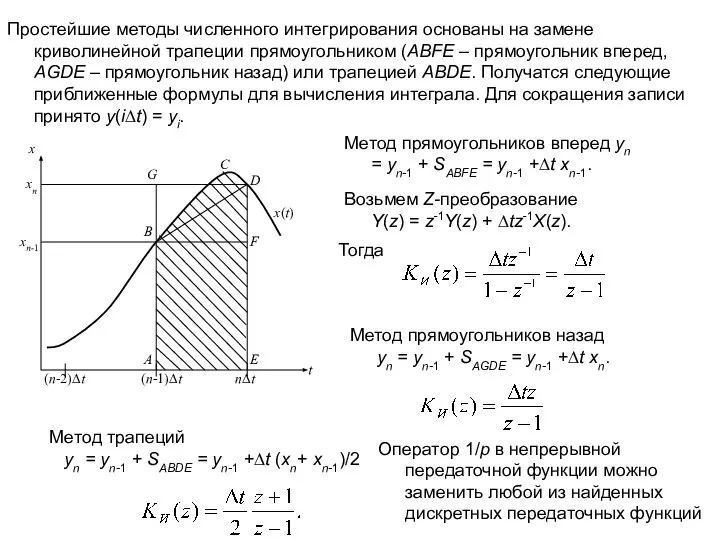
С учетом обозначений, принятых на рисунке

Простейшие методы численного интегрирования основаны на замене криволинейной трапеции прямоугольником (ABFE – прямоугольник вперед, AGDE – прямоугольник назад) или трапецией ABDE. Получатся следующие приближенные формулы для вычисления интеграла. Для сокращения записи принято y(i∆t) = yi.
Метод прямоугольников вперед yn = yn-1 + SABFE = yn-1 +∆t xn-1.
Метод прямоугольников назад yn = yn-1 + SAGDE = yn-1 +∆t xn.
Метод трапеций
yn = yn-1 + SABDE = yn-1 +∆t (xn+ xn-1)/2
Возьмем Z-преобразование Y(z) = z-1Y(z) + ∆tz-1X(z).
Тогда
Оператор 1/p в непрерывной передаточной функции можно заменить любой из найденных дискретных передаточных функций

Как видим, дискретная модель непрерывной системы может быть получена различными путями. Целесообразно выбрать самый точный. Практика моделирования показывает, что наименьшую ошибку обеспечивают методы численного интегрирования дифференциальных уравнений.