Содержание
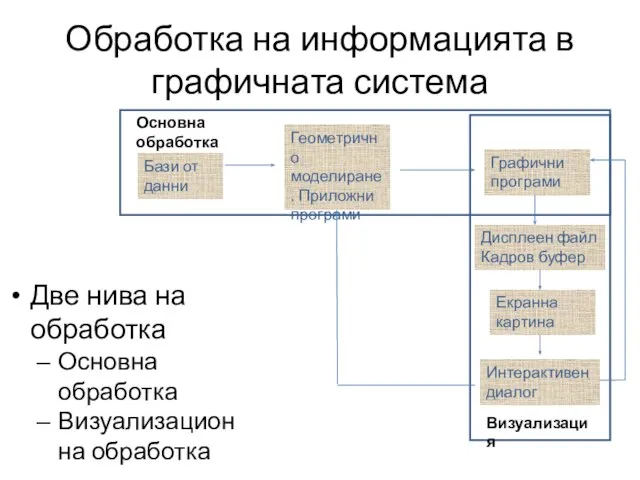
- 2. Обработка на информацията в графичната система Две нива на обработка Основна обработка Визуализационна обработка Основна обработка
- 3. Състав на дисплейната картина Графичните примитиви са основни графични елементи, които се използват за изграждане на
- 4. Графични примитиви - стандартен набор 1. Полилиния (Poliline) - представлява последователно свьрзани отсечки и се определя
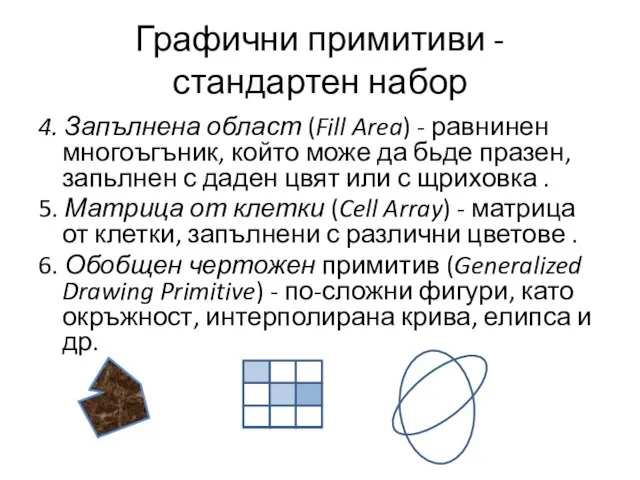
- 5. Графични примитиви - стандартен набор 4. Запълнена област (Fill Area) - равнинен многоъгъник, който може да
- 6. Графични примитиви - параметри Всеки примитив има три типа параметри: Геометрични – управляват формата и размера
- 7. Координатни системи
- 8. Моделен прозорец Всяка избрана моделна подобласт за визуализация на включените в тази подобласт обекти се нарича
- 9. Функция прозорец, функция изрязване Преобразуването на моделния прозорец в екранен образ се нарича функция прозорец. Друга
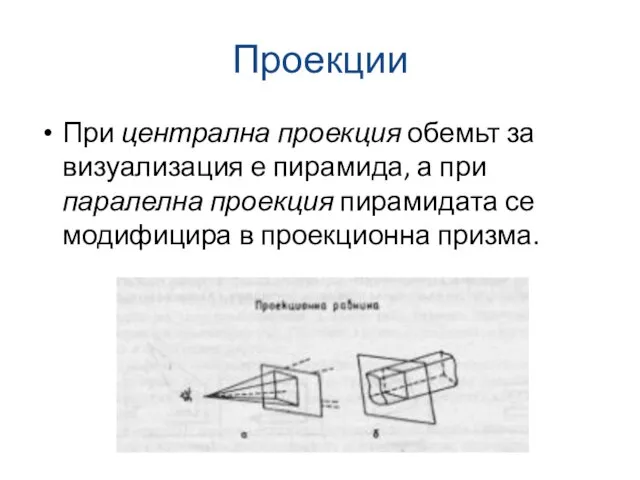
- 10. Проекции При централна проекция обемьт за визуализация е пирамида, а при паралелна проекция пирамидата се модифицира
- 11. Основни трансформации на картината Основни трансформации са: Транслация – преместване на картинен сегмент Ротация – завъртане
- 12. Производни трансформации а) разтягане или свиване по дадена ос - извьршва се чрез транслация на дадени
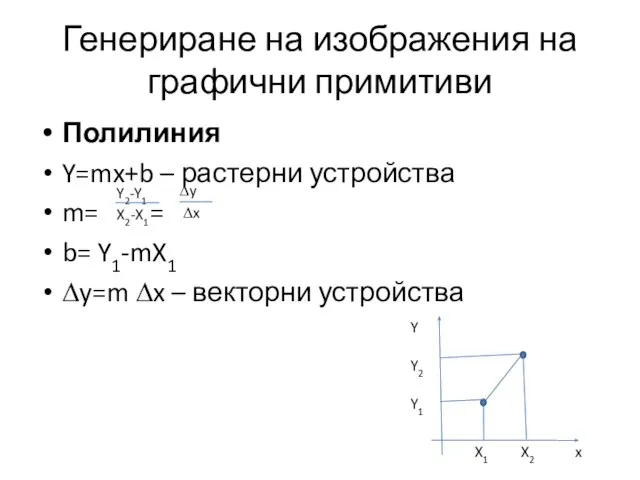
- 13. Генериране на изображения на графични примитиви Полилиния Y=mx+b – растерни устройства m= = b= Y1-mX1 ∆y=m
- 14. Генериране на изображения на графични примитиви Полилиния – алгоритъм на Брезенхайм Y=m(xi+1)+b d1=Y-yi=m(xi+1)+b-yi d2=(yi+1)-Y=yi+1-m(xi+1)-b d1-d2=2m(xi+1)-2yi+2b-1 p1=2∆y-
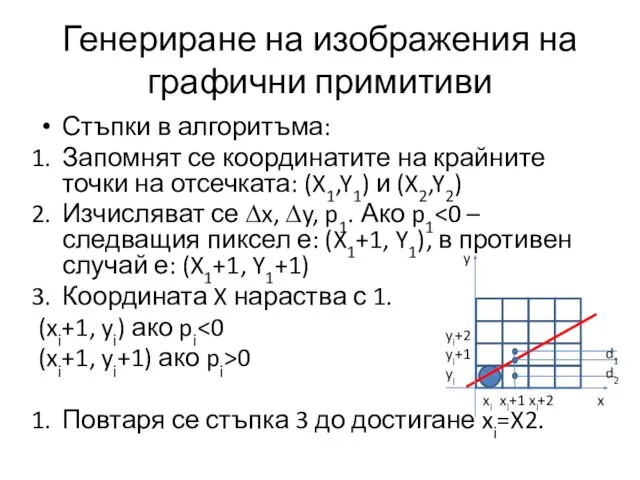
- 15. Генериране на изображения на графични примитиви Стъпки в алгоритъма: Запомнят се координатите на крайните точки на
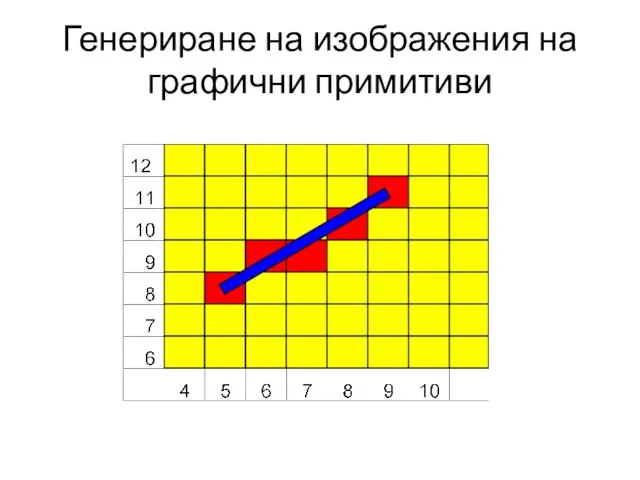
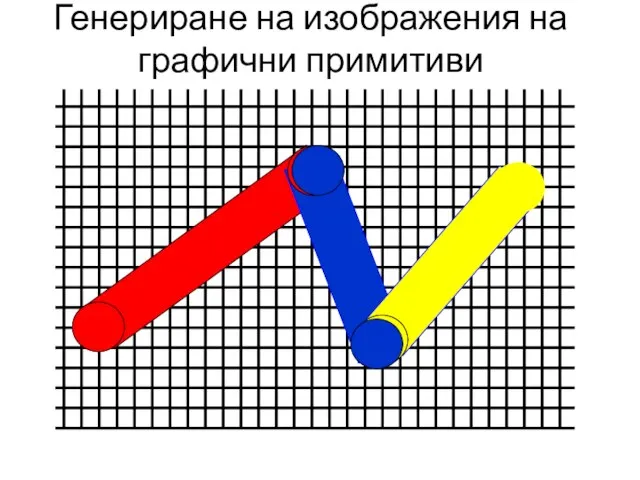
- 16. Генериране на изображения на графични примитиви
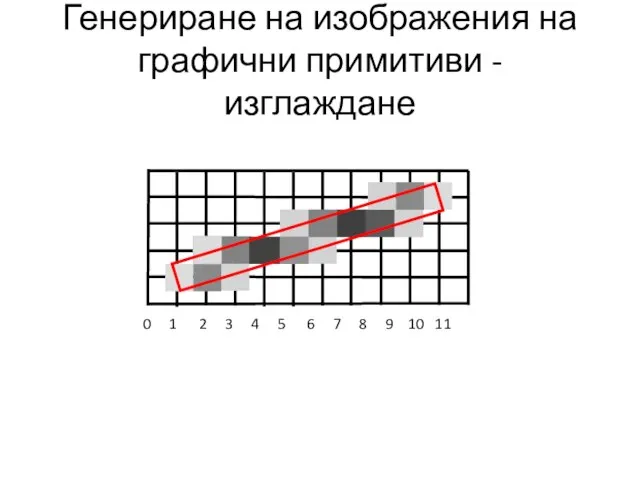
- 17. Генериране на изображения на графични примитиви - изглаждане 0 1 2 3 4 5 6 7
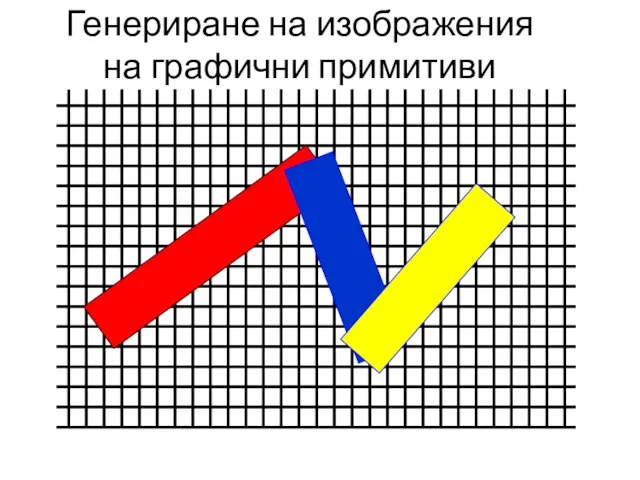
- 18. Генериране на изображения на графични примитиви
- 19. Генериране на изображения на графични примитиви
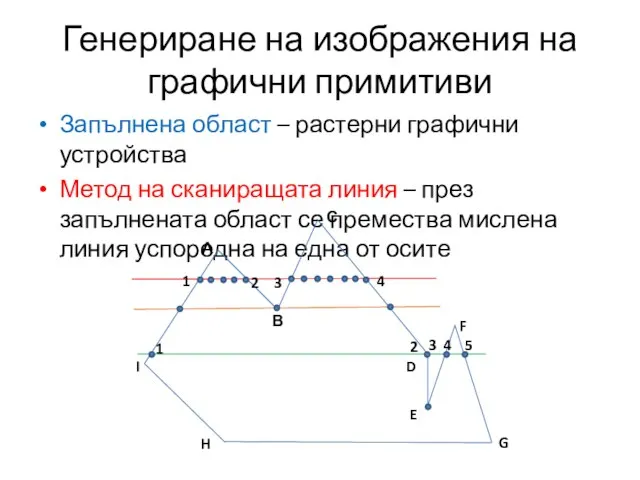
- 20. Генериране на изображения на графични примитиви Запълнена област – растерни графични устройства Метод на сканиращата линия
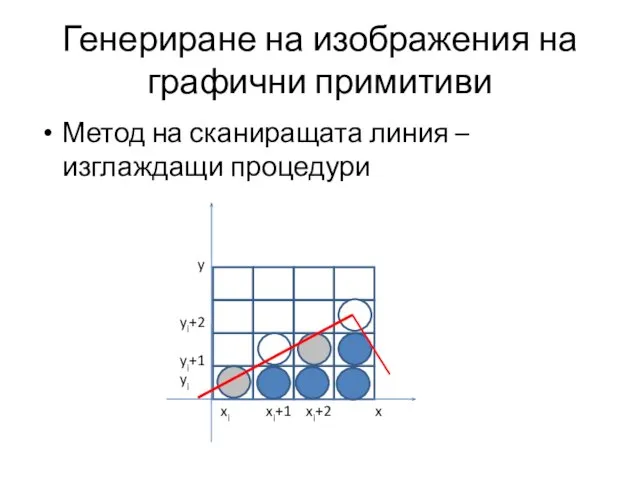
- 21. Генериране на изображения на графични примитиви Метод на сканиращата линия – изглаждащи процедури xi xi+1 xi+2
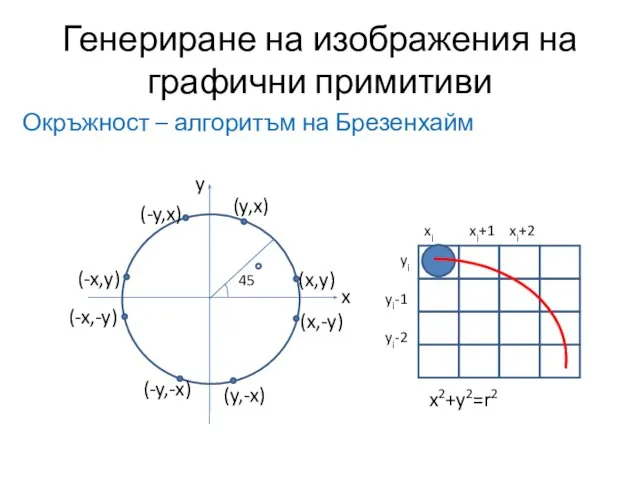
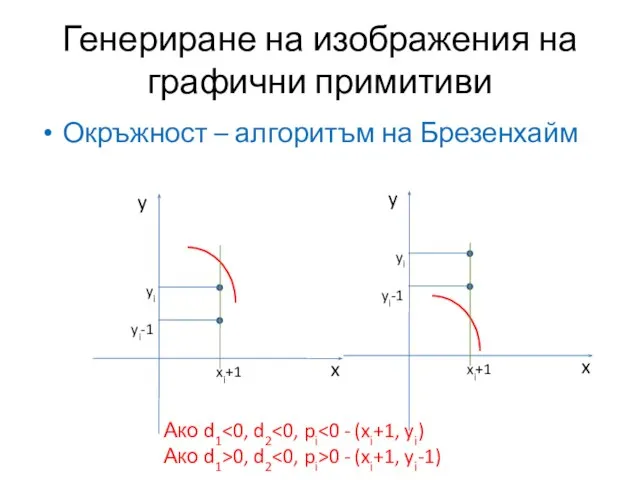
- 22. Генериране на изображения на графични примитиви Окръжност – алгоритъм на Брезенхайм
- 23. Генериране на изображения на графични примитиви Окръжност – алгоритъм на Брезенхайм d1 x y d2 xi+1
- 24. Генериране на изображения на графични примитиви Окръжност – алгоритъм на Брезенхайм Ако d1 Ако d1>0, d2
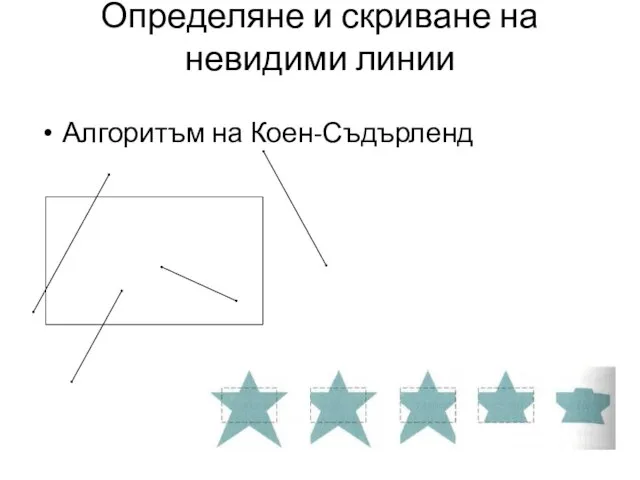
- 25. Определяне и скриване на невидими линии Алгоритъм на Коен-Съдърленд
- 27. Скачать презентацию










 Хоровод
Хоровод Обучение иностранным языкам по телефону и в сети Интернет ABBYY Language by phone
Обучение иностранным языкам по телефону и в сети Интернет ABBYY Language by phone Изменения в НК РФфевраль-ноябрь 2012
Изменения в НК РФфевраль-ноябрь 2012 Федеральная электронная торговая площадка, формы заявок, порядок проверки
Федеральная электронная торговая площадка, формы заявок, порядок проверки Simple, Compound, Complex and Compound-Complex Sentences in Your
Simple, Compound, Complex and Compound-Complex Sentences in Your Викторина театр и кино
Викторина театр и кино Найди еду. Квест
Найди еду. Квест 5ff46395-2c11-420a-8982-96dcb568b829
5ff46395-2c11-420a-8982-96dcb568b829 Владимирская гладь или верхошов
Владимирская гладь или верхошов Правила игры в футбол
Правила игры в футбол Дизайн в сфере применения
Дизайн в сфере применения Кредитная система
Кредитная система «Этим же объясняется отчасти и то плачевное положение, в котором оказался [Пациент], когда он выскочил из вагона и повалился на
«Этим же объясняется отчасти и то плачевное положение, в котором оказался [Пациент], когда он выскочил из вагона и повалился на  Rights and Freedoms of Man and Citizen in Russia
Rights and Freedoms of Man and Citizen in Russia Презентация на тему ДИНАМИКА ЦЕН НА ИМПОРТ
Презентация на тему ДИНАМИКА ЦЕН НА ИМПОРТ Flag of the United States
Flag of the United States  Семейная викторина
Семейная викторина Обособленные члены предложения в таблицах
Обособленные члены предложения в таблицах Презентация на тему Нация
Презентация на тему Нация  Электрофизические и электрохимические станки
Электрофизические и электрохимические станки Проектная технология на уроках информатики
Проектная технология на уроках информатики Гражданское право. Задачи для зачета
Гражданское право. Задачи для зачета Классификация предприятий и их характеристика
Классификация предприятий и их характеристика Predpriatia_obschestvennogo_pitania
Predpriatia_obschestvennogo_pitania Работа с глиной. Керамика
Работа с глиной. Керамика НОУ ВПО «Волгоградский институт бизнеса» ЦЕНТР БЕСПЛАТНОЙ ЮРИДИЧЕСКОЙ ПОМОЩИ ВОЛОНТЕРСКАЯ ОРГАНИЗАЦИЯ
НОУ ВПО «Волгоградский институт бизнеса» ЦЕНТР БЕСПЛАТНОЙ ЮРИДИЧЕСКОЙ ПОМОЩИ ВОЛОНТЕРСКАЯ ОРГАНИЗАЦИЯ Мои права и жизнь
Мои права и жизнь Памятка по составлению претензий
Памятка по составлению претензий