Содержание
- 2. Теория автоматов Абстрактный автомат Абстрактный автомат – позволяет абстрагироваться от конкретной схемы, можно рассматривать как «черный
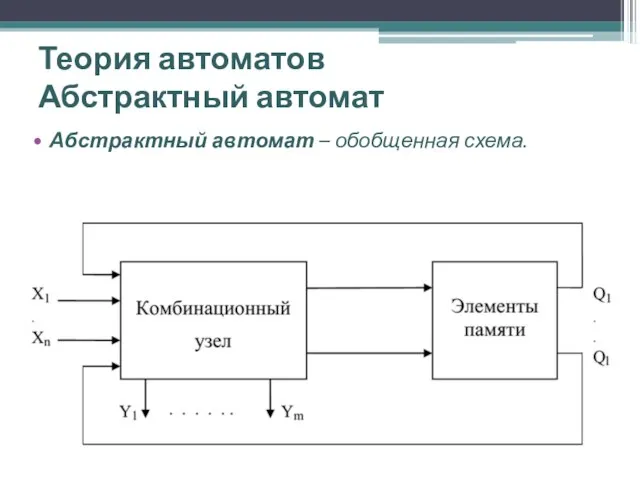
- 3. Теория автоматов Абстрактный автомат Абстрактный автомат – обобщенная схема.
- 5. Теория автоматов Автомат Мили. В автомате Мили функция выходов λ определяет значение выходного символа по классической
- 6. Теория автоматов Автомат Мили. a(t +1) = δ[a(t), x(t)] y(t) = λ [a(t), x(t)]
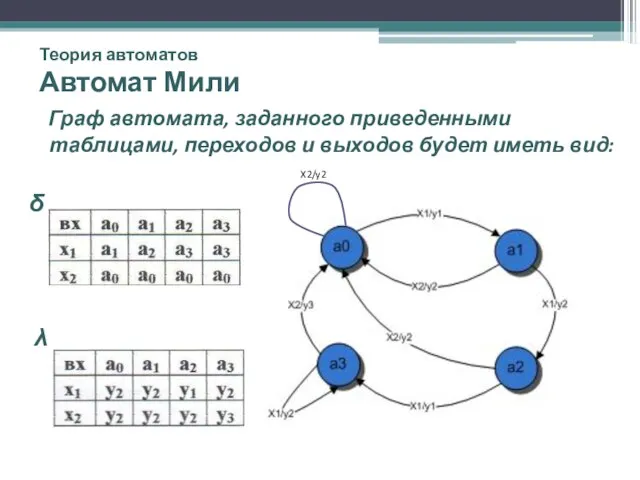
- 7. Теория автоматов Автомат Мили Граф автомата, заданного приведенными таблицами, переходов и выходов будет иметь вид: δ
- 8. Теория автоматов Автомат Мура. Зависимость выходного сигнала только от состояния автомата представлена в автоматах Мура. В
- 9. Теория автоматов Автомат Мура. a(t +1) = δ[a(t), x(t)] y(t) = λ [a(t)]
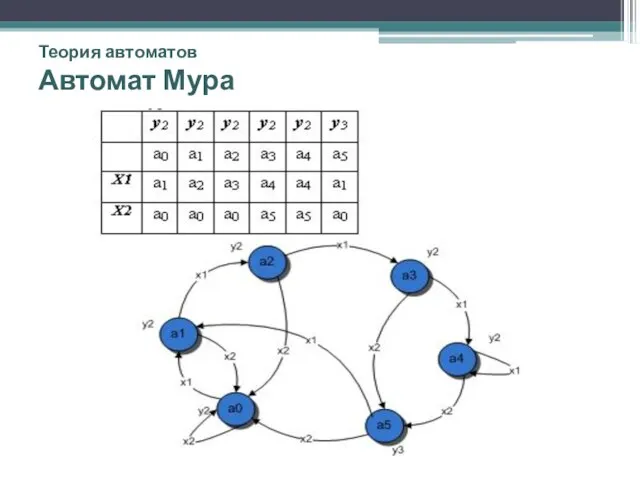
- 10. Теория автоматов Автомат Мура
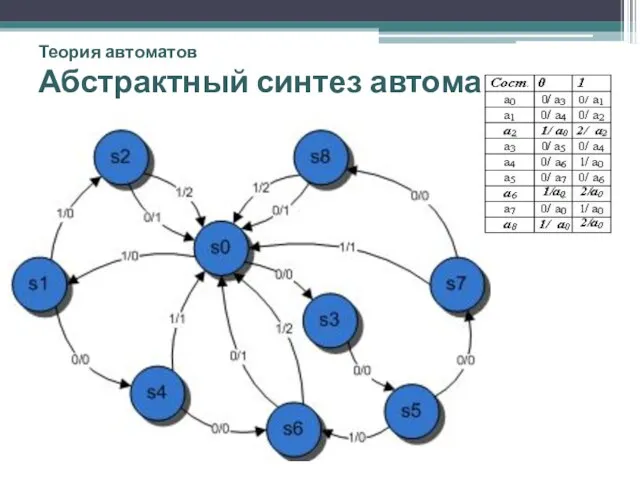
- 11. Теория автоматов Абстрактный синтез автоматов Задача структурного синтеза состоит в построении схемы автомата минимальной сложности. На
- 12. Теория автоматов Абстрактный синтез автоматов
- 13. Теория автоматов Абстрактный синтез автоматов Для упрощения автомата в первую очередь необходимо выделить эквивалентные состояния. Условия
- 14. Теория автоматов Абстрактный синтез автоматов Далее необходимо рассмотреть все возможные пары состояний для каждого из классов
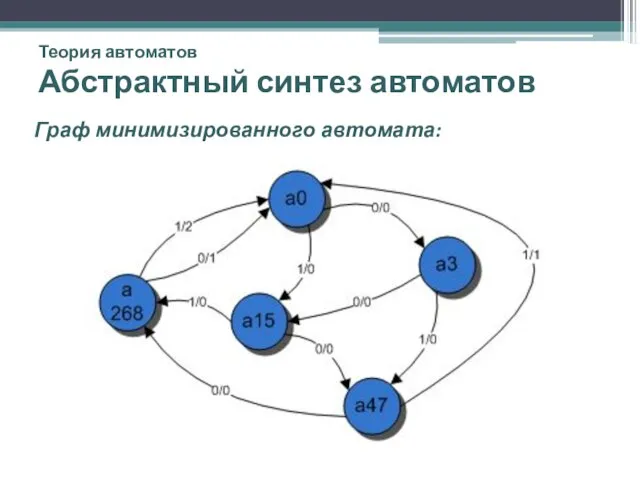
- 15. Теория автоматов Абстрактный синтез автоматов Граф минимизированного автомата:
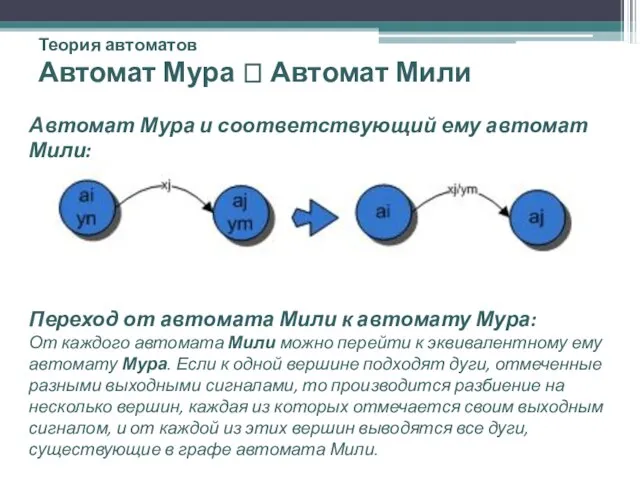
- 16. Теория автоматов Автомат Мура ? Автомат Мили Автомат Мура и соответствующий ему автомат Мили: Переход от
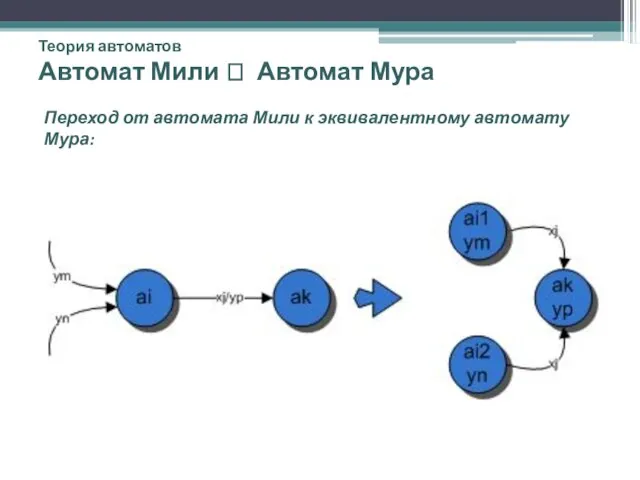
- 17. Теория автоматов Автомат Мили ? Автомат Мура Переход от автомата Мили к эквивалентному автомату Мура:
- 18. Теория автоматов Алгоритм синтеза конечных автоматов 1 шаг. Построение диаграммы переходов (графа конечного автомата). 2 шаг.
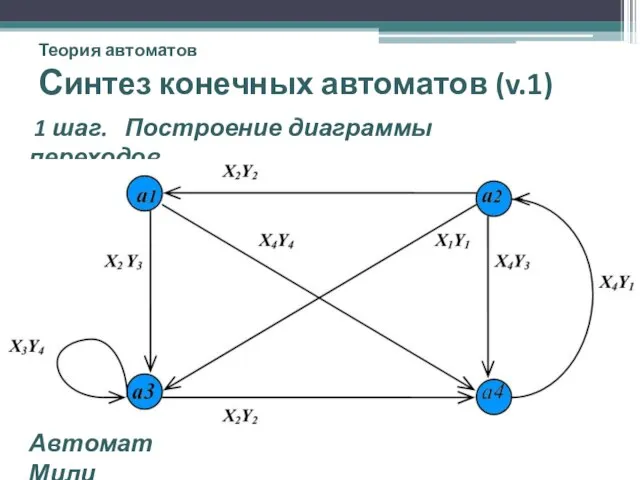
- 19. Теория автоматов Синтез конечных автоматов (v.1) 1 шаг. Построение диаграммы переходов. Автомат Мили
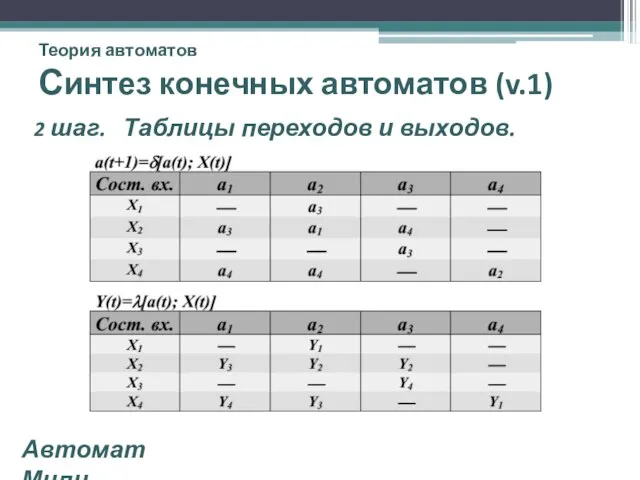
- 20. Теория автоматов Синтез конечных автоматов (v.1) 2 шаг. Таблицы переходов и выходов. Автомат Мили
- 21. Теория автоматов Синтез конечных автоматов (v.1) 3 шаг. Определение входных данных Автомат Мили
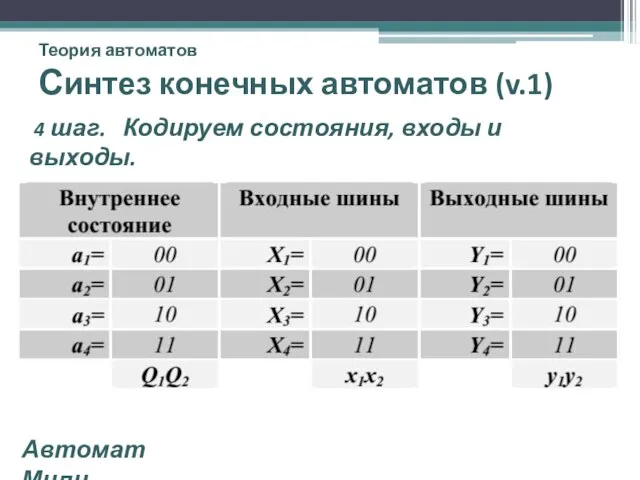
- 22. Теория автоматов Синтез конечных автоматов (v.1) 4 шаг. Кодируем состояния, входы и выходы. Автомат Мили
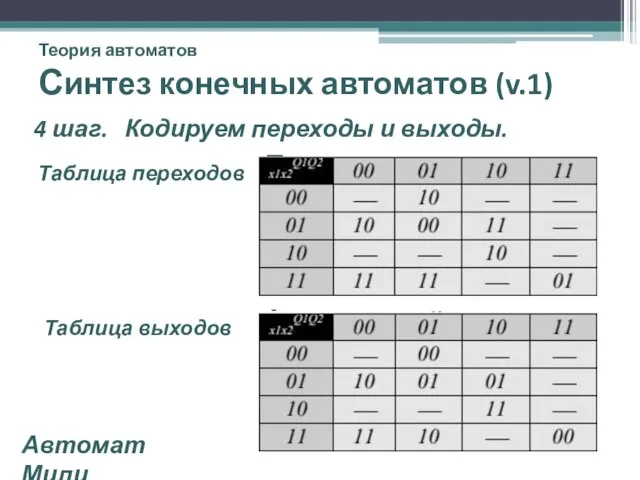
- 23. Теория автоматов Синтез конечных автоматов (v.1) 4 шаг. Кодируем переходы и выходы. Таблица переходов δ Таблица
- 24. Теория автоматов Синтез конечных автоматов (v.1) 5 шаг. Минимизация функций выходов. Автомат Мили
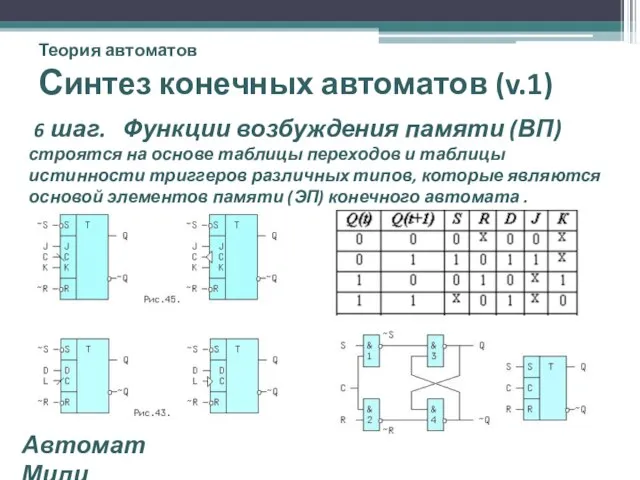
- 25. Теория автоматов Синтез конечных автоматов (v.1) 6 шаг. Функции возбуждения памяти (ВП) строятся на основе таблицы
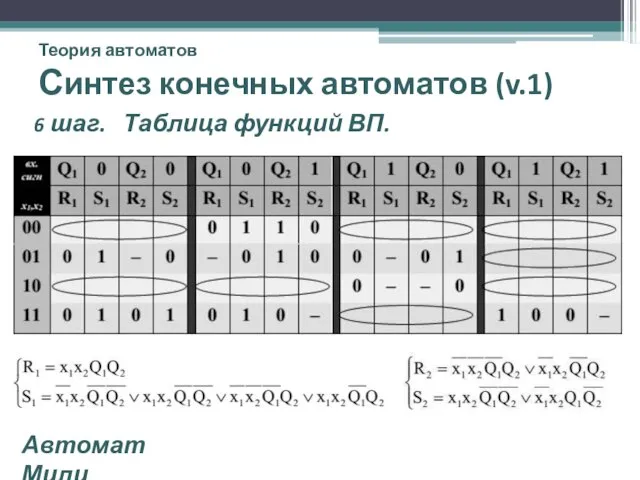
- 26. Теория автоматов Синтез конечных автоматов (v.1) 6 шаг. Таблица функций ВП. Автомат Мили
- 27. Теория автоматов Синтез конечных автоматов (v.1) 6 шаг. Минимизация функций ВП. Автомат Мили
- 28. Теория автоматов Синтез конечных автоматов (v.1) 7 шаг. Система уравнений (И-НЕ) – структура КА Автомат Мили
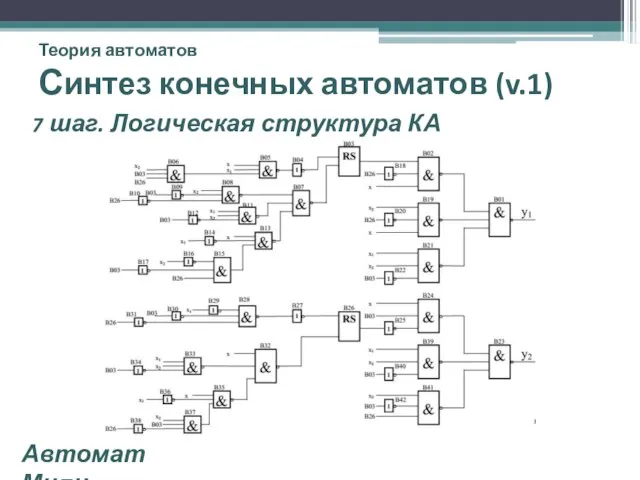
- 29. Теория автоматов Синтез конечных автоматов (v.1) 7 шаг. Логическая структура КА Автомат Мили
- 30. Теория автоматов Синтез конечных автоматов (v.1) 7 шаг. Система уравнений (И-НЕ) ? структура КА на ИС
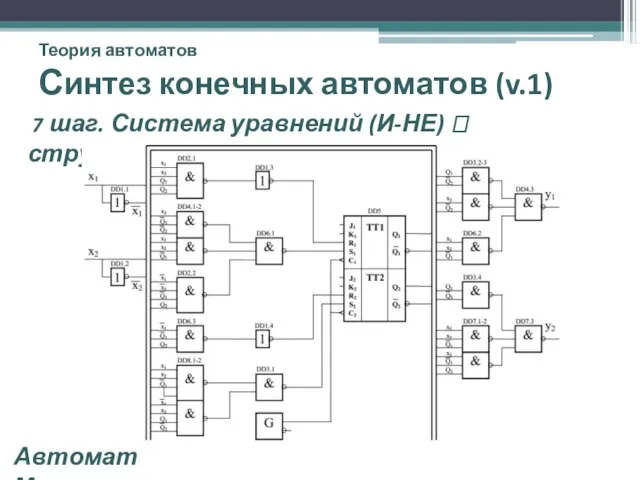
- 31. Теория автоматов Синтез конечных автоматов (v.1) 7 шаг. Система уравнений (И-НЕ) ? структура КА Автомат Мили
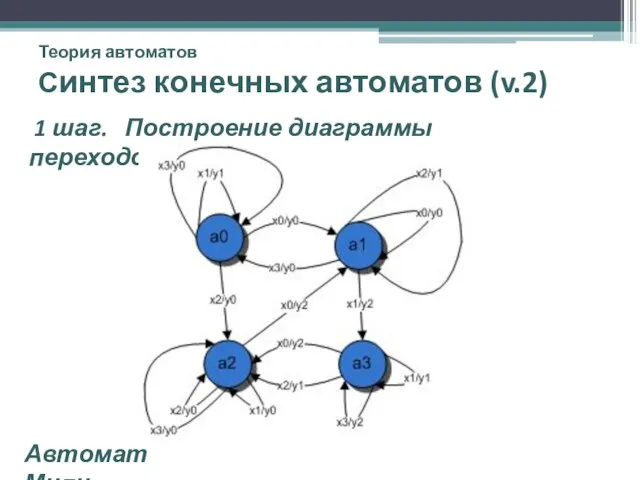
- 32. Теория автоматов Синтез конечных автоматов (v.2) 1 шаг. Построение диаграммы переходов. Автомат Мили
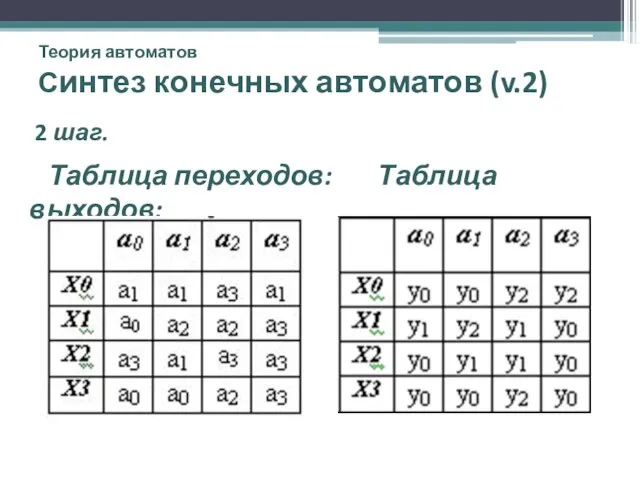
- 33. Теория автоматов Синтез конечных автоматов (v.2) 2 шаг. Таблица переходов: Таблица выходов:
- 34. Теория автоматов Синтез конечных автоматов (v.2) 3 шаг. Определение разрядности автомата. Число элементов памяти r: Число
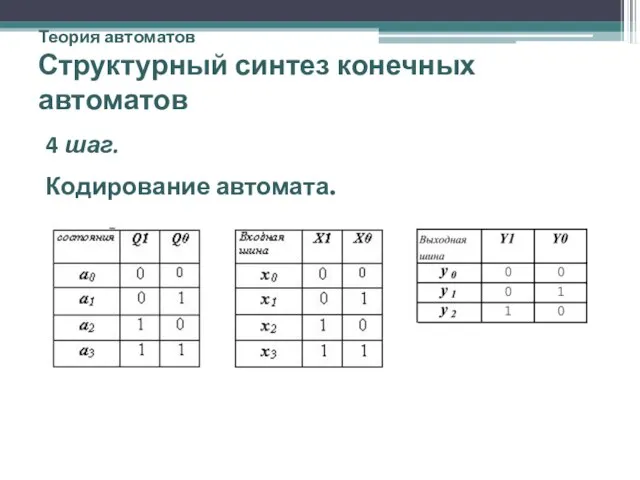
- 35. Теория автоматов Структурный синтез конечных автоматов 4 шаг. Кодирование автомата.
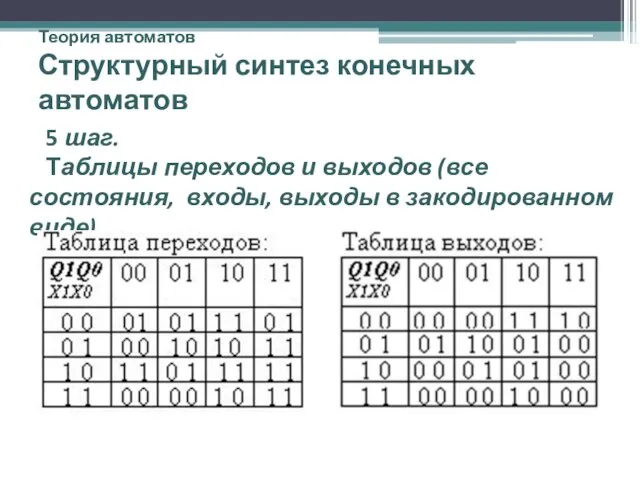
- 36. Теория автоматов Структурный синтез конечных автоматов 5 шаг. Таблицы переходов и выходов (все состояния, входы, выходы
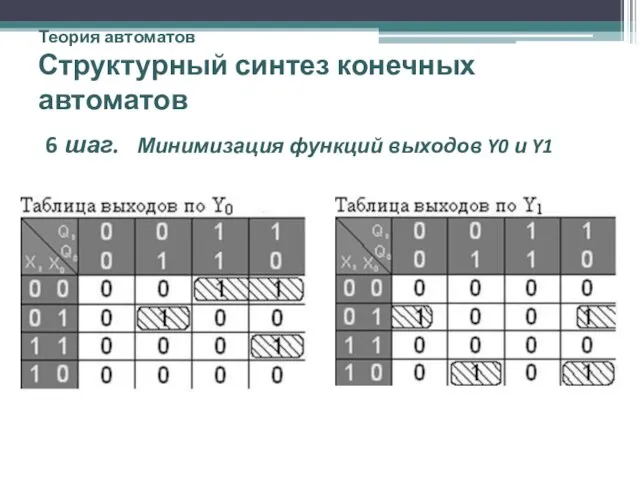
- 37. Теория автоматов Структурный синтез конечных автоматов 6 шаг. Минимизация функций выходов Y0 и Y1
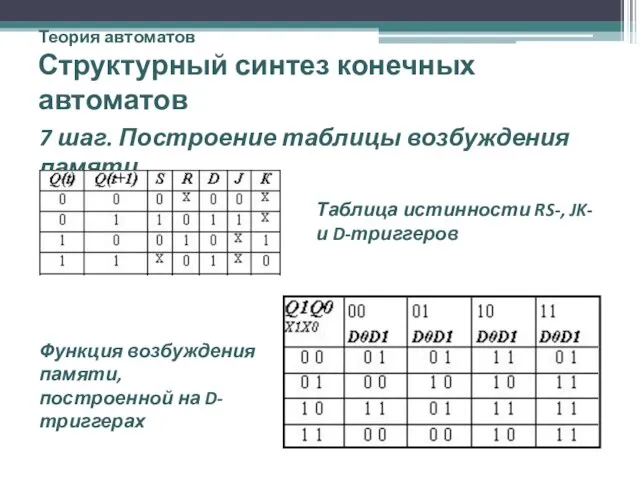
- 38. Теория автоматов Структурный синтез конечных автоматов 6 шаг. Получаем функции выходов: 7 шаг. Построение таблицы возбуждения
- 39. Теория автоматов Структурный синтез конечных автоматов 7 шаг. Построение таблицы возбуждения памяти Таблица истинности RS-, JK-
- 40. Теория автоматов Алгоритм синтеза конечных автоматов 7 шаг. Составляем и минимизируем функции ВП По таблица возбуждения
- 41. Теория автоматов Структурный синтез конечных автоматов 7 шаг. Получаем Функции возбуждения памяти D0 и D1 автомата,
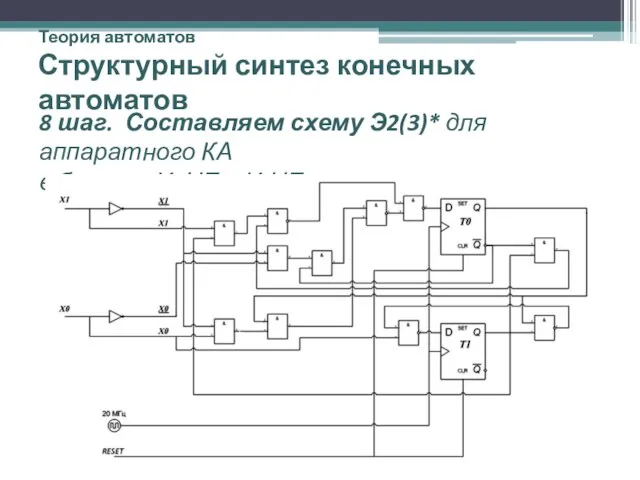
- 42. Теория автоматов Структурный синтез конечных автоматов 8 шаг. Составляем схему Э2(3)* для аппаратного КА в базисе
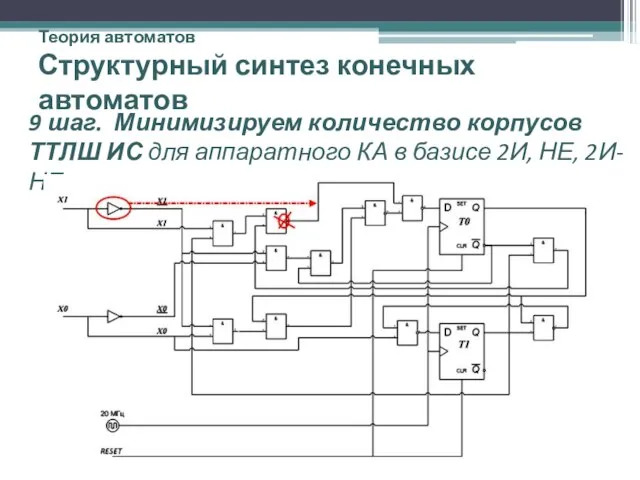
- 43. Теория автоматов Структурный синтез конечных автоматов 9 шаг. Минимизируем количество корпусов ТТЛШ ИС для аппаратного КА
- 44. Теория автоматов Синтез конечных автоматов на ПЛИС Основные задачи и цели PLD – Programmable logic devices
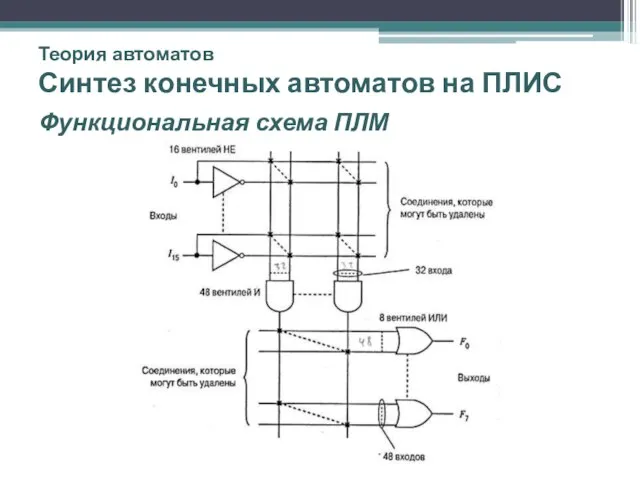
- 45. Теория автоматов Синтез конечных автоматов на ПЛИС Функциональная схема ПЛМ
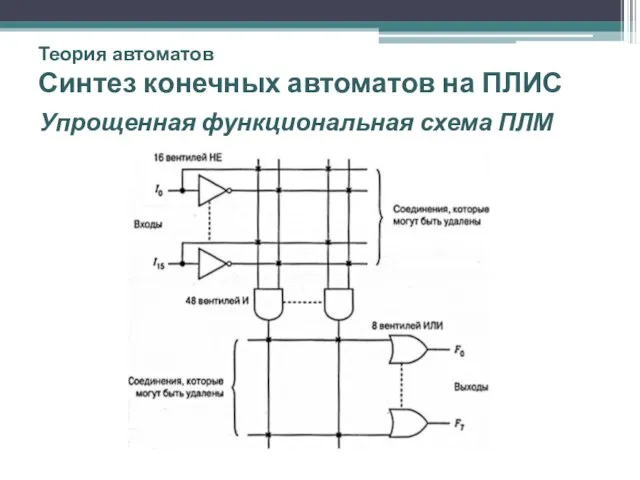
- 46. Теория автоматов Синтез конечных автоматов на ПЛИС Упрощенная функциональная схема ПЛМ
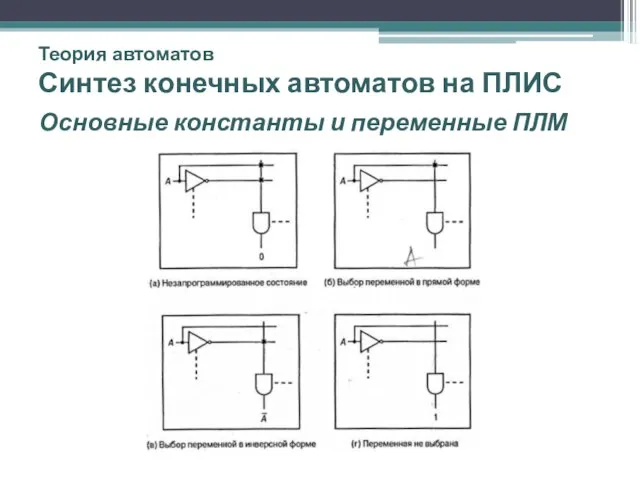
- 47. Теория автоматов Синтез конечных автоматов на ПЛИС Основные константы и переменные ПЛМ
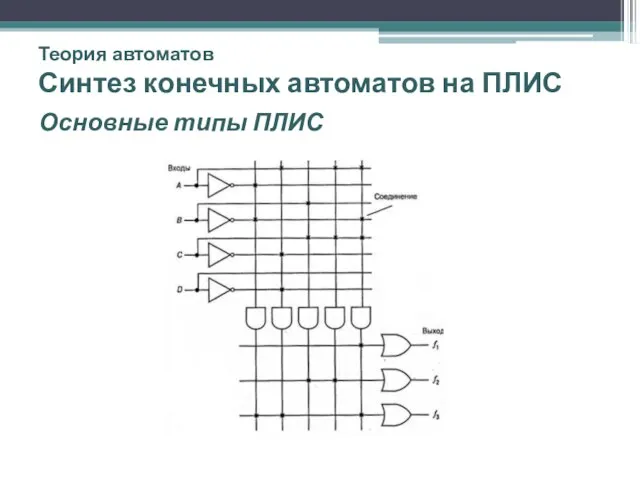
- 48. Теория автоматов Синтез конечных автоматов на ПЛИС Основные типы ПЛИС
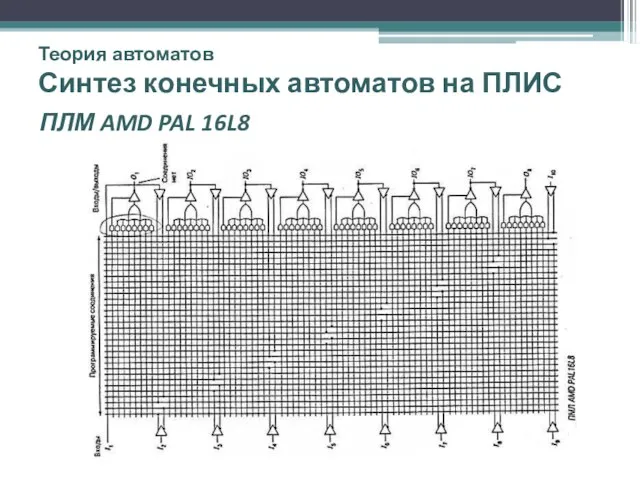
- 49. Теория автоматов Синтез конечных автоматов на ПЛИС ПЛМ AMD PAL 16L8
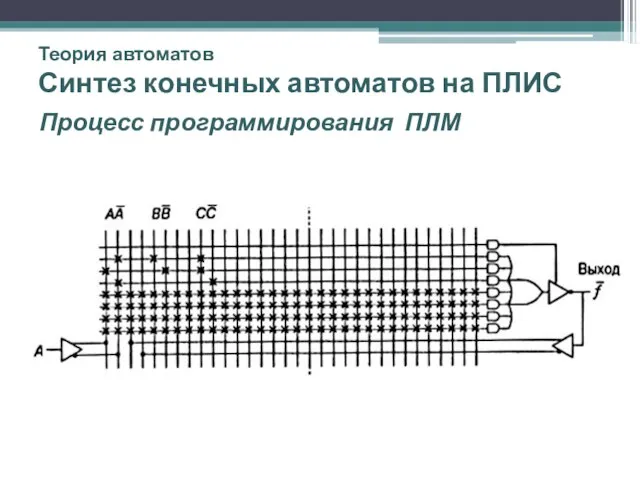
- 50. Теория автоматов Синтез конечных автоматов на ПЛИС Процесс программирования ПЛМ
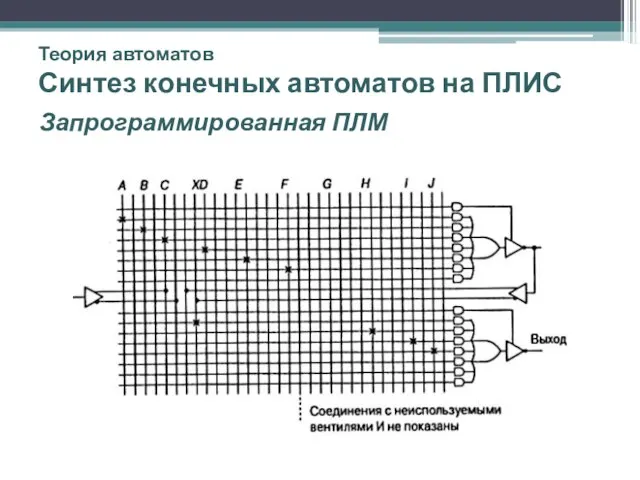
- 51. Теория автоматов Синтез конечных автоматов на ПЛИС Запрограммированная ПЛМ
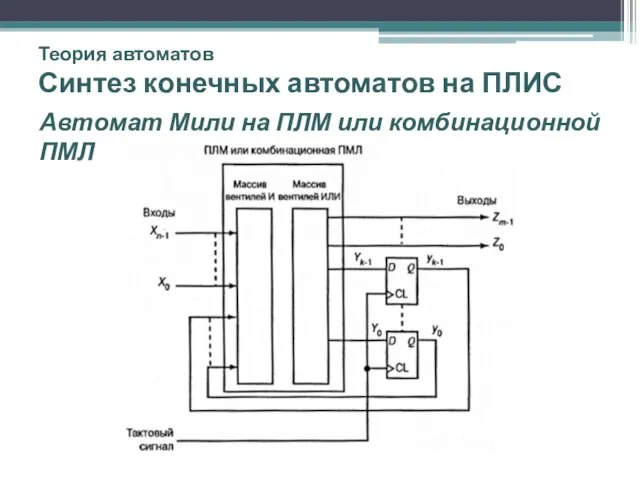
- 52. Теория автоматов Синтез конечных автоматов на ПЛИС Автомат Мили на ПЛМ или комбинационной ПМЛ
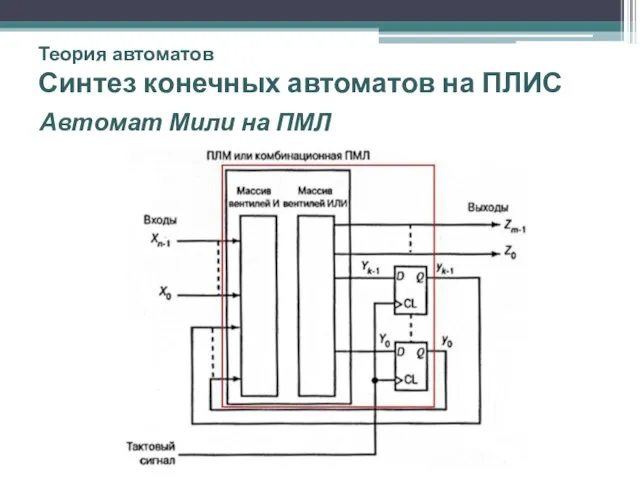
- 53. Теория автоматов Синтез конечных автоматов на ПЛИС Автомат Мили на ПМЛ
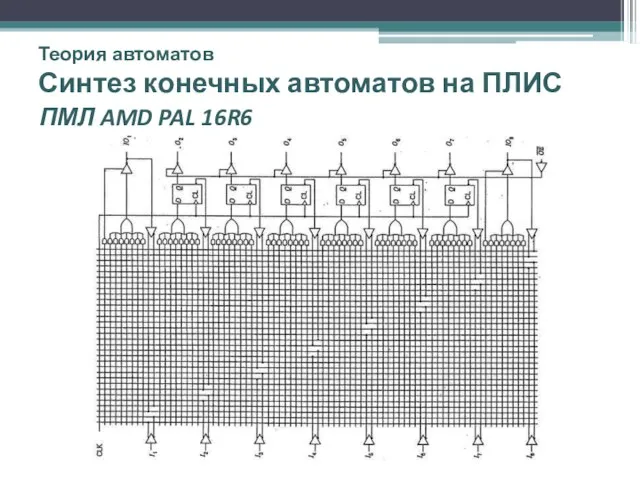
- 54. Теория автоматов Синтез конечных автоматов на ПЛИС ПМЛ AMD PAL 16R6
- 56. Скачать презентацию



![Теория автоматов Автомат Мили. a(t +1) = δ[a(t), x(t)] y(t) = λ [a(t), x(t)]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383606/slide-5.jpg)

![Теория автоматов Автомат Мура. a(t +1) = δ[a(t), x(t)] y(t) = λ [a(t)]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383606/slide-8.jpg)














 Презентация на тему Болезни Земли
Презентация на тему Болезни Земли Лес – природное сообщество
Лес – природное сообщество Вот это место
Вот это место Рекомендации по поддержке/коррекции имиджа с применением маркетинговых инструментов, брендинга, инструментов международного PR
Рекомендации по поддержке/коррекции имиджа с применением маркетинговых инструментов, брендинга, инструментов международного PR Презентация на тему Термины по обществознанию 6 класс
Презентация на тему Термины по обществознанию 6 класс Курение или здоровье -выбирайте сами!
Курение или здоровье -выбирайте сами! Поверхностное и коренное улучшение сенокосов и пастбищ
Поверхностное и коренное улучшение сенокосов и пастбищ Празнование нового года в Англии
Празнование нового года в Англии Биохимический состав плазмы крови
Биохимический состав плазмы крови «Применение производной и ознакомление с её прикладной частью ».
«Применение производной и ознакомление с её прикладной частью ». Техника графики
Техника графики ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ ТРЕХСЕКТОРНОЙ ИМИТАЦИОННОЙ МОДЕЛИ ОБЩЕГО РАВНОВЕСИЯ С ТЕНЕВЫМ ОБОРОТОМ
ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ ТРЕХСЕКТОРНОЙ ИМИТАЦИОННОЙ МОДЕЛИ ОБЩЕГО РАВНОВЕСИЯ С ТЕНЕВЫМ ОБОРОТОМ Внеигровые мероприятия в Российском университет
Внеигровые мероприятия в Российском университет Португалия
Португалия История развития спорта в посёлке Чернёво
История развития спорта в посёлке Чернёво Урок по творчеству шведской писательницы А.Линдгрен.
Урок по творчеству шведской писательницы А.Линдгрен. Предложение Группы компаний SIS для СТАДИОНОВ
Предложение Группы компаний SIS для СТАДИОНОВ Самый вкусный и ароматный бизнес
Самый вкусный и ароматный бизнес Классы органических веществ
Классы органических веществ Рентабельность запасов
Рентабельность запасов Органические вещества живых организмов
Органические вещества живых организмов Презентация на тему Экологические факторы
Презентация на тему Экологические факторы Презентация на тему Динозавры
Презентация на тему Динозавры Михаил Васильевич Ломоносов(1711-1765)Ученый, поэт.
Михаил Васильевич Ломоносов(1711-1765)Ученый, поэт. Презентация на тему Военная техника
Презентация на тему Военная техника Тест-тренажер: «НРАВСТВЕННОЕ СОЗНАНИЕ» Автор: Назаретьянц Надежда Хачатуровна, педагог-психолог высшей квалификационной категор
Тест-тренажер: «НРАВСТВЕННОЕ СОЗНАНИЕ» Автор: Назаретьянц Надежда Хачатуровна, педагог-психолог высшей квалификационной категор РЕЧЕВОЙ ЭТИКЕТ
РЕЧЕВОЙ ЭТИКЕТ Город Юрьев-Польский – это край родной!
Город Юрьев-Польский – это край родной!