Содержание
- 2. Хронология развития систем ЭЦП 1976 г. – открытие М. Хэлменом и У. Диффи асимметричных криптографических систем;
- 3. Односторонняя функция Пусть X и Y дискретные множества. Функция y=f(x), где x∈ X , y ∈
- 4. Пример односторонней функции функции Пусть p=7, a=3. Проверим, что a примитивный элемент - a1 =3(mod7), a2
- 5. Оценки сложности вычислений прямой и обратной функций Пусть 1000 разрядное двоичное число, тогда для решения задачи
- 6. Односторонняя функция с потайным ходом Это не просто ОФ, обращение которой невозможно, она содержит потайной ход
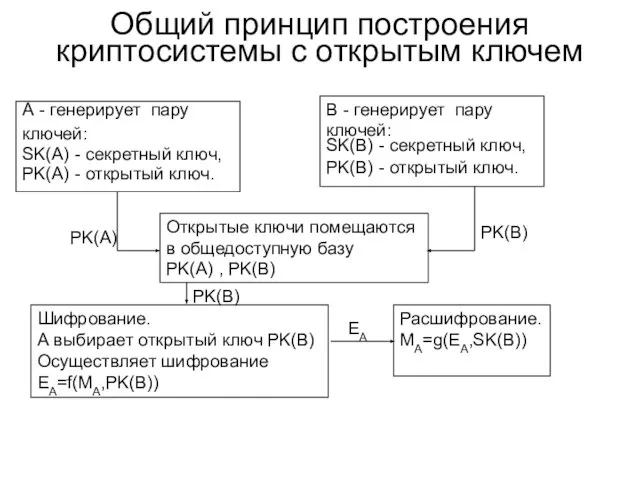
- 7. Общий принцип построения криптосиcтемы с открытым ключем А - генерирует пару ключей: SK(A) - секретный ключ,
- 8. Требования к системам с открытым ключем 1. Вычисление пары ключей PK, SK должно быть просто решаемой
- 9. Система шифрования Эль-Гамаля Пусть p -простое число; a - примитивный элемент. Генерирование пары открытых ключей A
- 10. Система шифрования Эль-Гамаля Расшифрование сообщения. Корр.А вычисляет c1x (modp) = akx (modp) , Затем находит c2akx
- 11. Стойкость системы Эль-Гамаля 1. Раскрытие секретного ключа эквивалентно решению задачи дискретного логарифмирования. 2. Нахождение m без
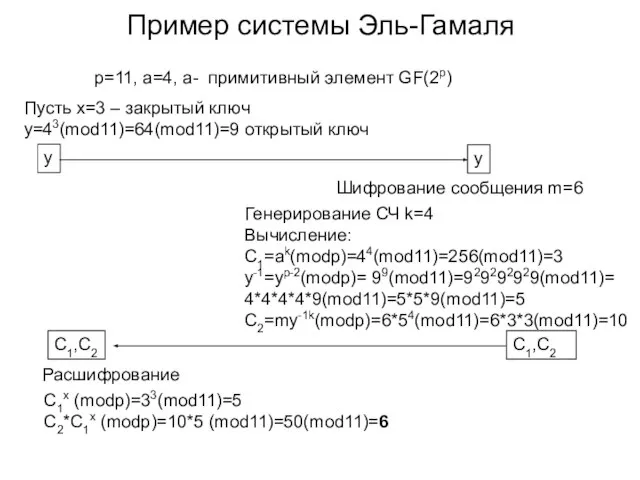
- 12. Пример системы Эль-Гамаля p=11, a=4, a- примитивный элемент GF(2p) Пусть x=3 – закрытый ключ y=43(mod11)=64(mod11)=9 открытый
- 13. Система РША (1978г.) Генерирование ключей. Случайно выбираются два простых числа p и q. Находится модуль N=pq.
- 14. Доказательство обратимости операции дешифрования операции шифрования Покажем, что Ed(modN) =(me)d(modN) =m По т. Эйлера mϕ(N)≡1(modN) для
- 15. Пример системы РША p=3, q=11 N=33 Генерирование ключей e=7, НОД(7,20)=1 d=7-1(mod20) = 3 Шифрование m=6 E=me(modN)=
- 16. Оценки стойкости системы РША 1. Нахождение чисел p и q по известному модулю N. Задача факторизации
- 17. Алгоритм формирования ключей на основе однонаправленных функций (алгоритм Диффи-Хеллмана)
- 20. Скачать презентацию















 Засели домики(игра-тренажёр)1 класс
Засели домики(игра-тренажёр)1 класс Партийный проект «ЭНЕРГЕТИЧЕСКАЯ БЕЗОПАСНОСТЬ»
Партийный проект «ЭНЕРГЕТИЧЕСКАЯ БЕЗОПАСНОСТЬ» Пластилин
Пластилин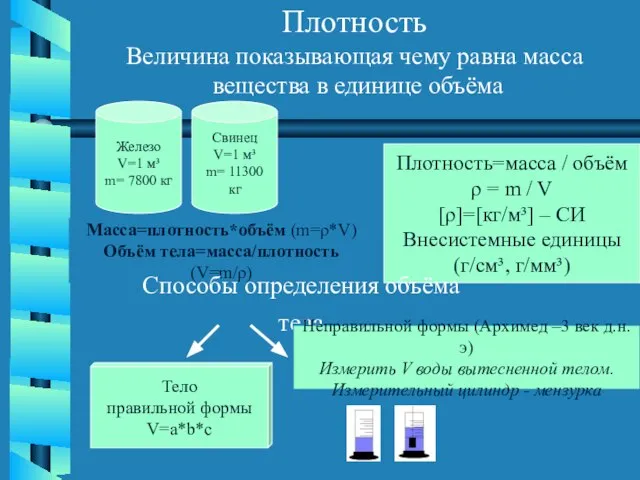 Плотность Величина показывающая чему равна масса вещества в единице объёма
Плотность Величина показывающая чему равна масса вещества в единице объёма «Определение шумового загрязнения на территории МОУ СОШ №12 г.Уфы»
«Определение шумового загрязнения на территории МОУ СОШ №12 г.Уфы» семья + to be - копия
семья + to be - копия Научно-техническая экспертиза инновационных проектов. Перспективы сотрудничества
Научно-техническая экспертиза инновационных проектов. Перспективы сотрудничества Содержание личных прав, свобод.
Содержание личных прав, свобод. ВКР: Арт-объект с использованием природного материала
ВКР: Арт-объект с использованием природного материала Отношения ЕС с Беларусью/Украиной
Отношения ЕС с Беларусью/Украиной Abstract painting
Abstract painting Cистема моментальной оплаты услуг
Cистема моментальной оплаты услуг Гражданин – свобода и ответственность (Свобода и ответственность несовершеннолетних граждан)
Гражданин – свобода и ответственность (Свобода и ответственность несовершеннолетних граждан) Оценка финансового состояния КБ
Оценка финансового состояния КБ Правила дорожного движения (5 класс)
Правила дорожного движения (5 класс) Обычаи и традиции казаков
Обычаи и традиции казаков Анализ заданий международных исследований ISA
Анализ заданий международных исследований ISA Наука и природа в творчестве
Наука и природа в творчестве Связь факторов темперамента со способностью к концентрации внимания
Связь факторов темперамента со способностью к концентрации внимания Тема: « Текст. Признаки текста»
Тема: « Текст. Признаки текста» Это вся моя родня…
Это вся моя родня… The Invention of the Automobile
The Invention of the Automobile Гроза. Молния
Гроза. Молния Культура Башкортостана
Культура Башкортостана Защита прав человека и основных свобод
Защита прав человека и основных свобод Профилактика предэкзаменационного стресса
Профилактика предэкзаменационного стресса 0066d18f43ec5674
0066d18f43ec5674 ПлитаЭффективность Индукция90 % Керамика58 - 60 % Электричество47 - 55 % Газ30 - 55 % …для того, чтобы электрическая плита закипятила воду та
ПлитаЭффективность Индукция90 % Керамика58 - 60 % Электричество47 - 55 % Газ30 - 55 % …для того, чтобы электрическая плита закипятила воду та