Круги Эйлера при решении логических задач .

Цель работы: исследовать множества чисел с точки зрения теории множеств, а именно операций над множествами и их изображения с помощью кругов Эйлера. Кроме того, исследовать возможные решения задач с помощью кругов Эйлера, то есть с помощью операций над множествами чисел, данных в задачах.
Объект исследования- множества.
Предмет исследования- круги Эйлера.

Задачи:
Изучить понятие «числовые множества» и их изображения.
Элементы множеств.
Пересечение множеств.
Объединение множеств.
Практическое применение кругов Эйлера при решении логических задач.

Ученый Леонард Эйлер придумал обозначать множества чисел кругами и они получили название «круги Эйлера».
Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 году, а умер в 1783 году) написал более 850 научных работ. В одной из них и появились эти круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». Наряду с кругами применяются прямоугольники и другие фигуры.

Обозначим множество натуральных чисел с помощью кругов Эйлера так:
N

Достаточно ли множества N для человека? Конечно, нет, так как не всегда можно выполнить вычитание во множестве натуральных чисел. Существуют и отрицательные числа, то есть числа … —3, —2, —1, каждое из которых противоположно какому – нибудь натуральному, Границей между натуральными числами и целыми отрицательными числами служит число 0, а все они вместе (натуральные, нуль и целые отрицательные) составляют новое числовое множество Z (от первой буквы немецкого слова zahl — число) — множество целых чисел.
Z
N

Обитаемый остров" и "Стиляги"
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
Ответ. 5 человек смотрели только «Стиляги».

Любимые мультфильмы
Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?

Решение
В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

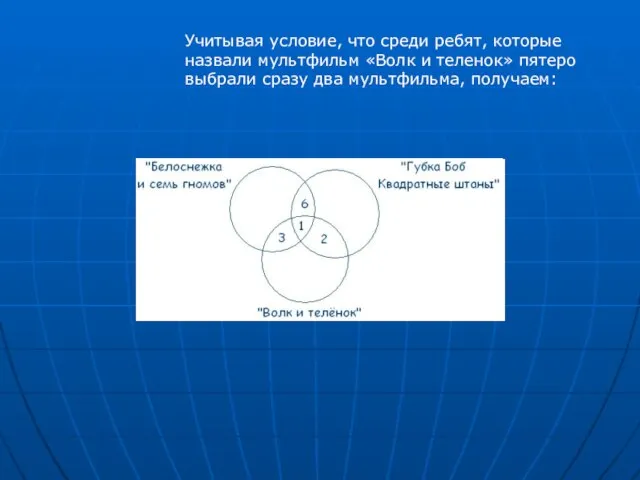
Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».

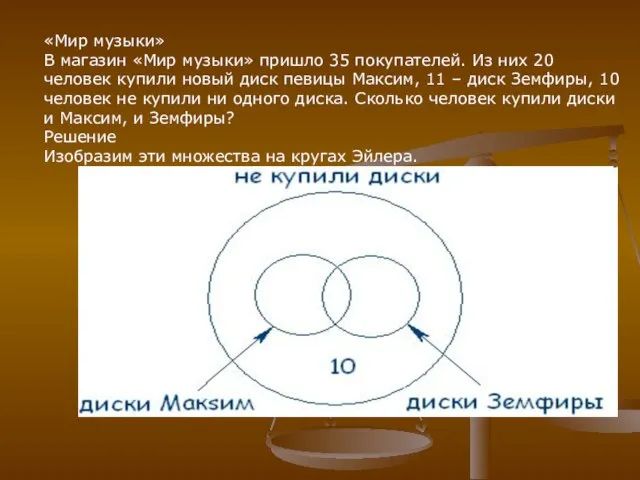
«Мир музыки»
В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
Решение
Изобразим эти множества на кругах Эйлера.

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:
Ответ: 6 покупателей купили диски и Максим, и Земфиры.