Квадратные уравнения

Цели:
1.Систематизация знаний по теме «Квадратные уравнения»; 2.Развитие интереса к предмету.
Задачи:
1.Знать определение квадратного уравнения, типы, методы решения; 2.Понимать отличительные особенности квадратных уравнений; 3.Применять полученные знания при решении рациональных, иррациональных уравнений, сокращении дробей, решении задач.

Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

325 – 409 г.г. по Р. Х. знаменитый александрийский математик.
ДИОФАНТ
В арифметике Диофанта отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Задача Диофанта
Найти два числа, зная, что их сумма равна 20, а произведение — 96.
Если бы искомые числа были равны:
То произведение чисел было бы равно 100
ПРОТИВОРЕЧИЕ
С
УСЛОВИЕМ!!!

Найти два числа, зная, что их сумма равна 20, а произведение — 96.
Значит, одно из этих чисел будет больше половины их суммы, т. е. (10 + х),
другое же меньше, т. е. (10 – х).
Разность между ними 2х.
Отсюда уравнение:
(10+x)(10—x) =96,
100 —x2 = 96.
x2 - 4 = 0
х = 2
Одно из искомых чисел равно 12, другое 8.
Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Интересные способы решения квадратных уравнений встречаются в трудах индийского ученого Бхаскары
(600 – около 680г.г.).
И арабского ученого
Ал – Хорезми
(780 – около 850г.г.)

Задача знаменитого индийского математика XII в. Бхаскары:
Обезьянок резвых стая всласть поевши, развлекалась, их в квадрате часть восьмая на поляне забавлялась, а двенадцать по лианам стали прыгать, повисая. Сколько ж было обезьянок, ты скажи мне, в этой стае?

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений.
Бхаскара пишет:
x2 - 64x = - 768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 1024, получая затем:
x2 - 64х + 1024 = -768 + 1024,
(х - 32)2 = 256,
х - 32= ±16,
x1 = 16, x2 = 48.

Квадрат и число 21 равны 10 корням. Найти корень (подразумевается корень уравнения х2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Задача Ал – Хорезми:

Квадратным уравнением называется уравнение вида
где коэффициенты a,b,c-любые действительные числа, причем
Определение квадратного уравнения

Определение корня
Корнем квадратного уравнения
называют такое значение переменной х, при котором квадратный трехчлен
обращается в нуль;

Типы квадратных уравнений
полные
неполные
а)
б)
в)

a)9х2=0;
б)3x+ x2+1=0;
в)2x2-32=0;
г) x2+4x=0;
д)2х2+5х-7=0;
е)12-х2+3х=0.
Данные уравнения разбейте на полные и неполные:

а) 9х2= 0;
в) 2х2-32=0;
г) х2+4х=0.
б) 3х+х2+1=0;
д)2х2+5х-7=0;
е)12-х2+3х=0.
неполные:
полные:

Способы решения неполных квадратных уравнений
c=0
b=0
b=0;c=0

Решите уравнения:

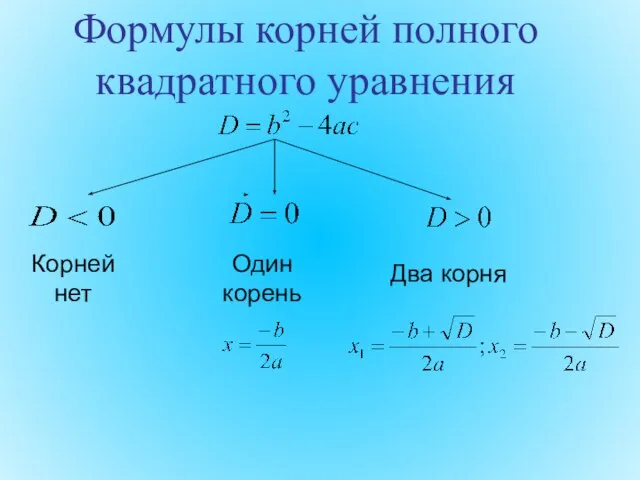
Формулы корней полного квадратного уравнения
Корней нет
Один корень
Два корня

Формула четного коэффициента
b=2k
a=1

Теорема Виета
- корни квадратного уравнения

1.Найдите корни квадратного уравнения, не используя формулы корней:
Корней нет
2.Составьте приведенное квадратное уравнение, корнями которого являются числа 3 и -7:

Применение квадратных уравнений
-решение рациональных уравнений;
-решение иррациональных уравнений;
-решение задач;
-разложение квадратного трехчлена на множители;
-сокращение дробей.

1.Решите уравнения:
2.Сократите дробь:
3.При каком значении параметра a уравнение имеет один корень?
Задание:

Проверь себя!
Ответ: 1;2.

Проверь себя!
Корней нет
Ответ: -4;4.

Проверь себя!
Проверка:
Ответ: 1.
-2-посторонний корень

Проверь себя!
2.Сократить дробь:

Проверь себя!
Квадратное уравнение имеет один корень, если D=0;
Ответ: а=-6;а=6.
3.

Составьте математическую модель для решения задачи:
В прямоугольном треугольнике один катет меньше гипотенузы на 4 см, а другой – на 8 см. Найдите гипотенузу.

Домашнее задание:
1.Решите уравнения:
2.Сократите дробь:
3.При каком значении параметра а уравнение имеет один корень?