Содержание
- 2. Кв. уравнения в Древнем Вавилоне. Главное меню Необходимость решать уравнения не только первой, но и второй
- 3. Кв. уравнения в Индии. Главное меню Задачи на квадратные уравнения встречаются уже в 499 г. В
- 4. Квадратные уравнения в Европе 13-17 в.в. Главное меню Формулы решения квадратных уравнений в Европе были впервые
- 5. Определение Главное меню Уравнение вида ax2+bx+c=0, где a, b, c - действительные числа, причем a не
- 6. Неполные кв. уравнения Главное меню Если в квадратном уравнении ax2+bx+c=0 второй коэффициент b или свободный член
- 7. Полное квадратное уравнение Главное меню Если в квадратном уравнении второй коэффициент и свободный член не равны
- 8. Теорема Виета Главное меню Теорема. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным
- 9. Теорема, обратная теореме Виета. Главное меню Теорема. Если числа m и n таковы, что их сумма
- 10. Кв. уравнения с комплексными переменными Главное меню Сначала рассмотрим простейшее кв. уравнение где a-заданное число, а
- 11. Решение кв. уравнений с помощью графиков. Главное меню Не используя формул квадратное уравнение можно решить графическим
- 12. Разложение кв. трехчлена на множители Главное меню Многочлен вида ax2+bx+c, где a,b,c - некоторые числа, x
- 13. Применение кв. уравнений Главное меню Решение квадратных уравнений широко применяется в других разделах математики: в разложении
- 14. Стр.1 Практикум Главное меню Неполные кв. уравнения Далее
- 15. Стр.2 Практикум Главное меню Метод выделения полного квадрата. Далее
- 16. Стр.3 Практикум Главное меню Решение кв. уравнений по формуле b2-4ac Далее
- 17. Стр.4 Практикум Главное меню Приведённые кв. уравнения. Теорема Виета Записать приведённое кв. уравнение, имеющее корни :
- 18. Стр.5 Практикум Главное меню Решение кв. уравнений по теореме обратной т. Виета Далее 1)Составьте уравнение, если
- 19. Стр.6 Практикум Главное меню Решение задач с помощью кв. уравнений. Процессы Скорость км/ч Время ч. Расстояние
- 20. Стр.7 Практикум Главное меню Решение задач с помощью кв. уравнений. Процессы Скорость км/ч Время ч. Расстояние
- 21. Стр.8 Практикум Главное меню Решение задач с помощью кв. уравнений. Было Изменилось Стало Первый год 20000
- 22. Стр.9 Практикум Главное меню Решение кв. уравнений по формуле k2-ac. т.к. D1 Ответ: К.Н. Ответ: Ответ:
- 24. Скачать презентацию





















 Презентация на тему Опасна ли гроза
Презентация на тему Опасна ли гроза Redaktiruemy_beydzh
Redaktiruemy_beydzh Физкультура. Виды плаванья
Физкультура. Виды плаванья О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС
О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС Письмо пером - за и против
Письмо пером - за и против Tin cup design
Tin cup design Транспорт. Виды транспорта
Транспорт. Виды транспорта Новый стандарт: обучаем и учимся
Новый стандарт: обучаем и учимся Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации
Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации Виды рабочей одежды
Виды рабочей одежды Я люблю тебя, Сакский район!
Я люблю тебя, Сакский район! Что такое значение?От П.Грайса к теории игр.
Что такое значение?От П.Грайса к теории игр. Тема лекции:«Прикладная информатика в табличном процессоре»
Тема лекции:«Прикладная информатика в табличном процессоре»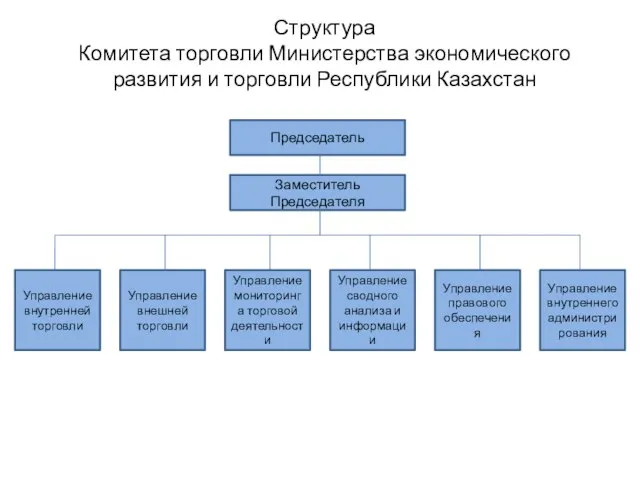 Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан
Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан Презентация на тему Информация в природе, обществе и технике
Презентация на тему Информация в природе, обществе и технике Основы коммуникативной компетентности педагогов
Основы коммуникативной компетентности педагогов Хочу отдыхать
Хочу отдыхать Урок по рассказам И.А. Бунина о любви
Урок по рассказам И.А. Бунина о любви Русская изба – поэтапное рисование
Русская изба – поэтапное рисование Известные люди Австрии
Известные люди Австрии 3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012
3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012 Викторина по произведениям А.П.Чехова « Смешные рассказы»
Викторина по произведениям А.П.Чехова « Смешные рассказы» Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г.
Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г. ЮТА (2)
ЮТА (2) Многообразие компьютеров
Многообразие компьютеров Похищение человека
Похищение человека Понятие и особенности административно правовой нормы
Понятие и особенности административно правовой нормы Техника мраморирования в современном дизайне
Техника мраморирования в современном дизайне