Содержание
- 2. Корпускулярно-хвильовий дуалізм. Рівняння Шредингера 1. Гіпотеза де-Бройля. 2. Дифракція електронів. 3. Співвідношення невизначеностей. 4. Часове і
- 3. Формула де-Бройля Оскільки світло проявляє корпускулярно-хвильовий дуалізм, Луї де-Бройль в 1924 р. висунув гіпотезу, що і
- 4. Формула де-Бройля Якщо нерелятивістська частинка має кінетичну енергію Тоді Отже, для електронів, розігнаних до 1÷100 еВ
- 5. Формула де-Бройля Подивимось з позицій корпускулярно-хвильового дуалізму на атом водню. Згідно з другим постулатом Бора mυrn
- 6. Стаціонарна орбіта
- 7. Формула де-Бройля При проходженні окремих електронів через тонкий монокристал отримуємо дифракційну картину. Отже, хвильові властивості притаманні
- 8. Співвідношення невизначеностей Розглянемо обмеження, які накладає корпускулярно-хвильовий дуалізм на можливість одночасного визначення імпульсу та координати частинок
- 9. Співвідношення невизначеностей. Такі ж висновки справедливі і для частинок. В 1927 р. В.Гейзенберг знайшов співвідношення Добуток
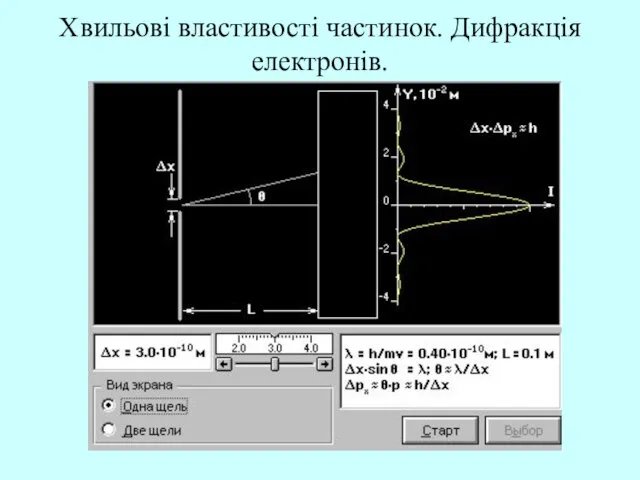
- 10. Хвильові властивості частинок. Дифракція електронів.
- 11. Співвідношення невизначеностей Розглянемо електрон в атомі. Його положення визначається з точністю до розмірів атома Δх ~
- 12. Хвильова функція Потрібно з'ясувати фізичну природу хвиль де-Бройля. Порівнювали дифракцію світла і мікрочастинки. Для світла в
- 13. Хвильова функція Отже, дифракційна картина є проявом статистичної закономірності, згідно з якою частинки потрапили в ті
- 14. Хвильова функція Звідси − умова нормування хвильової функції. Щоб функція ψ була характеристикою стану частинки, необхідно:
- 15. Хвильова функція Якщо система може знаходитись в станах ψ1, ψ2, ..., ψn, то вона може бути
- 16. Хвильова функція Одноелектронну хвильову функцію в сферично симетричному електричному полі атомного ядра, яку задають головним n,
- 17. Хвильова функція Геометричне уявлення атомної орбіталі – область простору, обмежена поверхнею рівною густини (еквіденсітною поверхнею) ймовірності
- 18. Хвильова функція Орбіталі слетеровського типу мають наступний вигляд: де A − коефіцієнт норміровки − сферична гармоніка
- 19. Густина електричного заряду У квантовій механіці густина заряду, наприклад, електрона в атомі, співвідноситься з хвильової функцією
- 20. Метод МО ЛКАО Молекула розглядається як ціле, а не як сукупність атомів, що зберегли індивідуальність. Всі
- 21. ОРБІТАЛЬ – область найбільш можливого місцезнаходження електрона в атомі (атомна орбіталь) або в молекулі (молекулярна орбіталь).
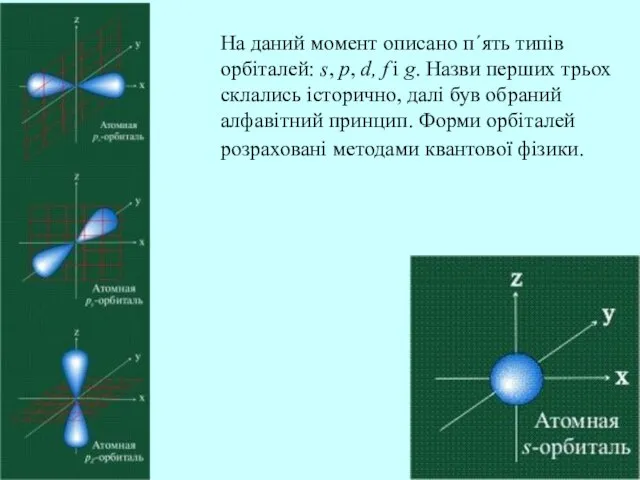
- 22. На даний момент описано п΄ять типів орбіталей: s, p, d, f і g. Назви перших трьох
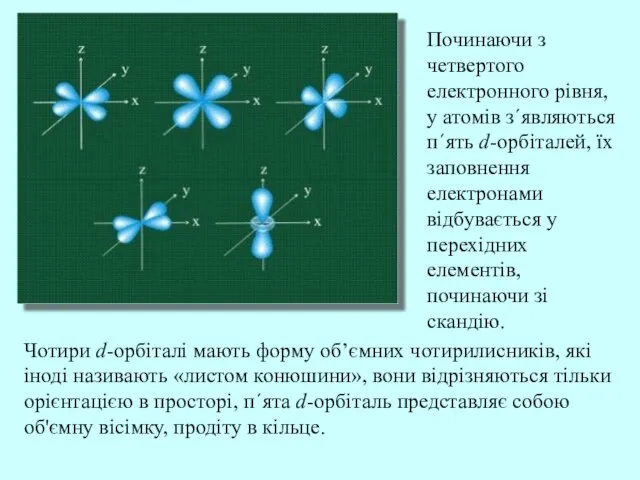
- 23. Чотири d-орбіталі мають форму об’ємних чотирилисників, які іноді називають «листом конюшини», вони відрізняються тільки орієнтацією в
- 24. В тому випадку, коли атом вуглецю бере участь в утворенні насичених сполучень (які не мають кратних
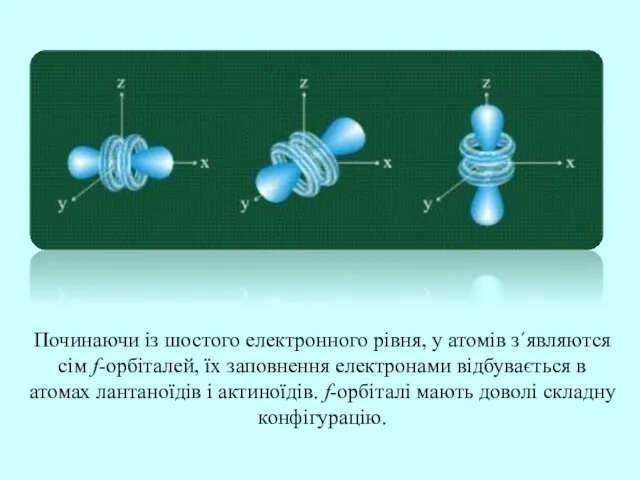
- 25. Починаючи із шостого електронного рівня, у атомів з΄являются сім f-орбіталей, їх заповнення електронами відбувається в атомах
- 26. На восьмому електронному рівні знаходяться дев΄ять g-орбіталей. Елементи, які мають електрони на цих орбіталях, повинні з'явитися
- 27. Хімічний зв’язок Хімічний зв'язок притягання між атомами або молекулами дозволяє утворення хімічних сполук, які містять два
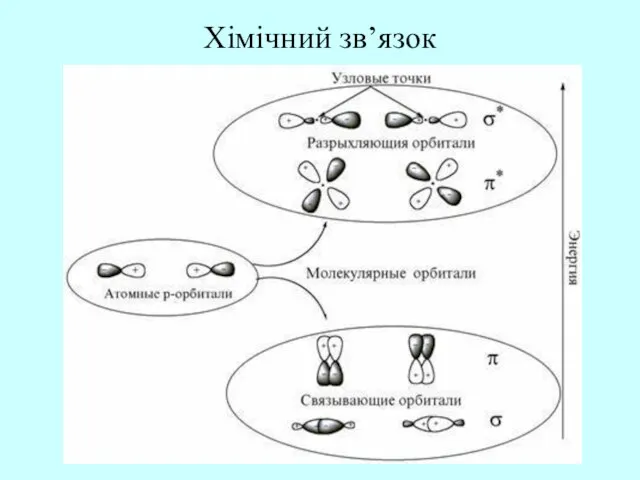
- 28. Хімічний зв’язок
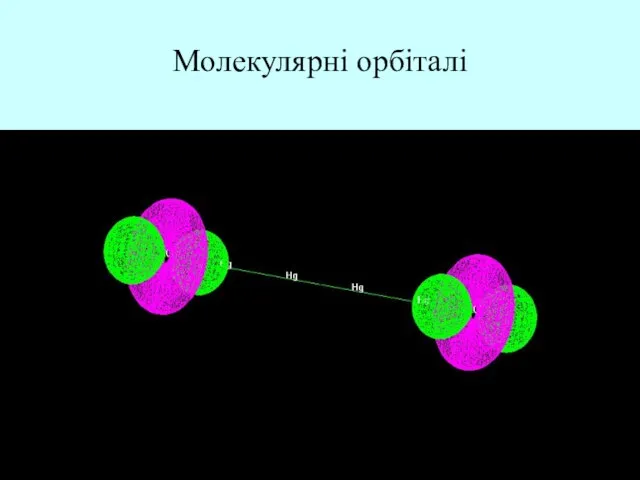
- 29. Молекулярні орбіталі
- 30. Молекулярні орбіталі
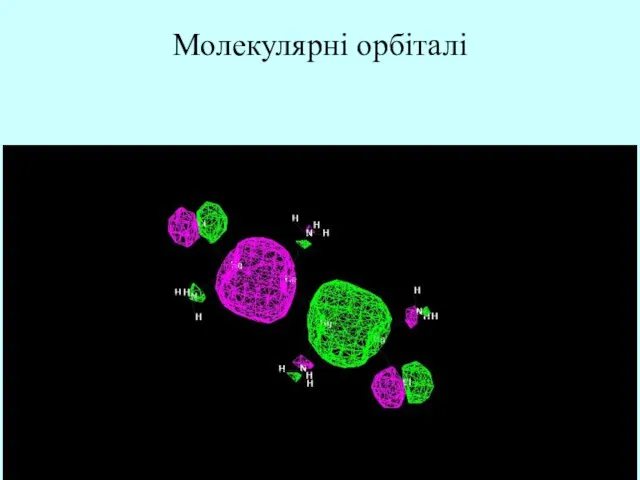
- 31. Молекулярні орбіталі
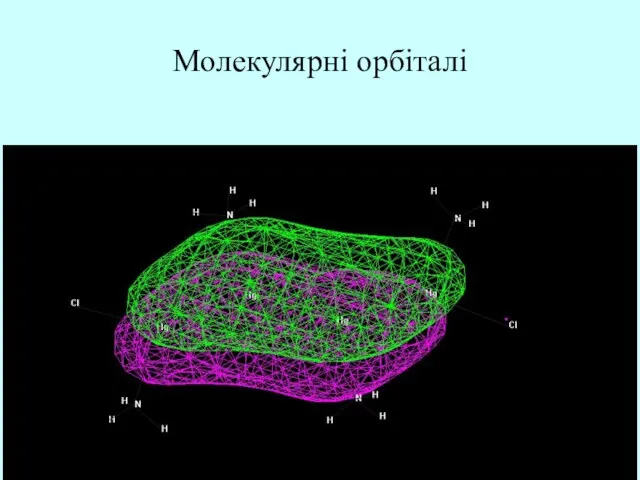
- 32. Молекулярні орбіталі
- 33. Молекулярні орбіталі
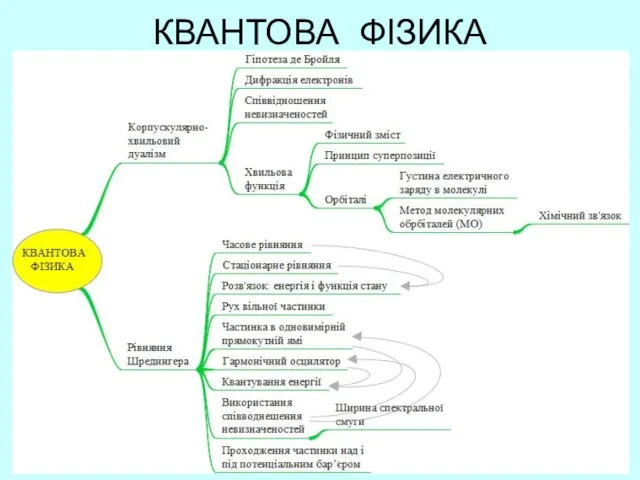
- 34. КВАНТОВА ФІЗИКА
- 35. Квантово-механічні задачі 1. Рівняння Шредінґера 2. Рух вільної частинки. 3. Частинка в одновимірній прямокутній потенціальній ямі.
- 36. Рівняння Шредінгера Хвилі де-Бройля мають статистичне трактування. Цей факт та співвідношення невизначеностей вимагають, щоб рівняння руху
- 37. Рівняння Шредінгера Таке рівняння справедливе для довільної частинки з v Розглянемо вільну частинку, якій відповідає хвиля
- 38. Рівняння Шредінгера Знайдемо похідні Звідси Ці дані підставимо в формулу
- 39. Рівняння Шредінгера Такий же вигляд має рівняння Шредінгера при U = 0. Якщо існує силове поле,
- 40. Стаціонарне рівняння Шредінгера Шукаємо розв'язок у вигляді Підставивши в рівняння Шредінгера, отримаємо Це і є стаціонарне
- 41. Рух вільної частинки Застосуємо рівняння Шредінгера до руху вільної частинки. Енергія E = Ek. Частинний розв'язок:
- 42. Рух вільної частинки Маємо суперпозицію двох плоских хвиль однакової частоти ω = Е/ħ. Порівняння з виразом
- 43. Рух вільної частинки Ймовірність знайти частинку в певній точці простору Отже, як і слід чекати для
- 44. Частинка в одновимірній прямокутній потенціальній ямі Розглянемо прямокутну потенціальну яму, для якої Рівняння Шредінгера Яма має
- 45. Частинка в одновимірній прямокутній потенціальній ямі В межах ями Розв'язок Оскільки ψ(0) = 0, то В
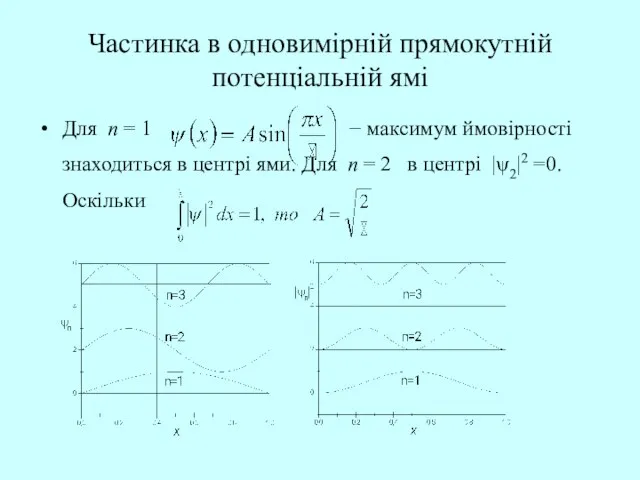
- 46. Частинка в одновимірній прямокутній потенціальній ямі Для n = 1 − максимум ймовірності знаходиться в центрі
- 47. Частинка в одновимірній прямокутній потенціальній ямі Різниця енергій двох сусідніх рівнів збільшується зі збільшенням n. Якщо
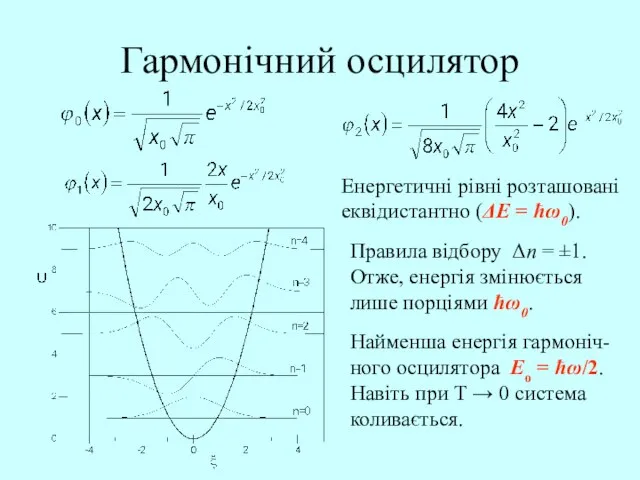
- 48. Гармонічний осцилятор Хвильове рівняння, яке описує гармонічний осцилятор, має вигляд: Розв’язком цього рівняння є: En =
- 49. Гармонічний осцилятор Енергетичні рівні розташовані еквідистантно (ΔE = ћω0). Правила відбору Δn = ±1. Отже, енергія
- 50. Використання співвідношення невизначеностей Розрахуємо співвідношення невизначеностей для розрахунку енергій в одновимірній потенціальній ямі та для гармонічного
- 51. Використання співвідношення невизначеностей Тепер розрахуємо енергію гармонічного осцилятора: Звідси
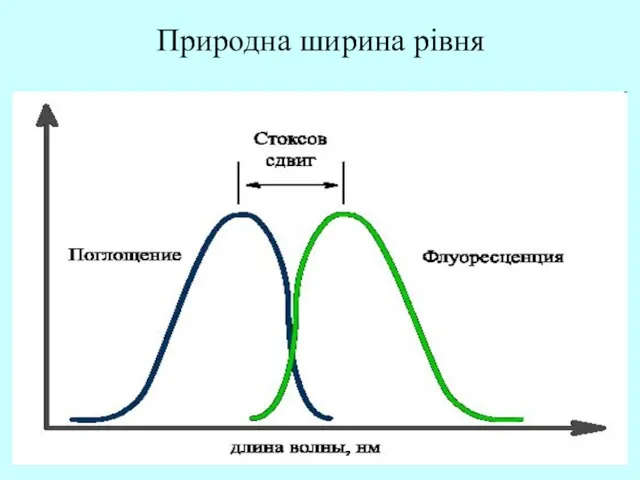
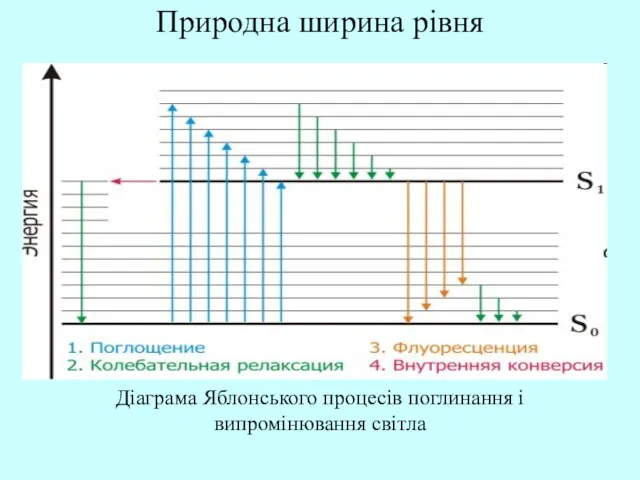
- 52. Природна ширина рівня
- 53. Природна ширина рівня Діаграма Яблонського процесів поглинання і випромінювання світла
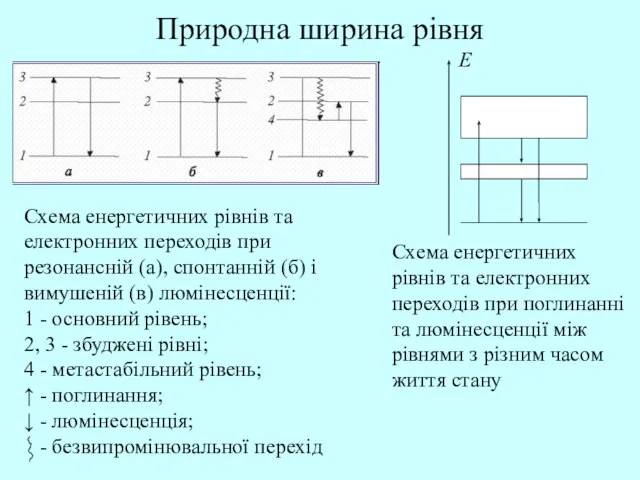
- 54. Схема енергетичних рівнів та електронних переходів при резонансній (а), спонтанній (б) і вимушеній (в) люмінесценції: 1
- 55. Природна ширина рівня ШИРИНА РІВНЯ – невизначеність енергії квантово-механічної системи (атома, молекули та ін), що має
- 56. Природна ширина рівня Час життя Δτ, а отже, і ширина рівня обумовлені можливістю квантових переходів системи
- 57. Тунельний ефект Розглянемо бар'єр прямокутної форми на шляху руху частинок. В класичній фізиці частинка з E
- 58. Тунельний ефект Для областей 1 і 3 Для області 2 Розв'язок В області 3 є лише
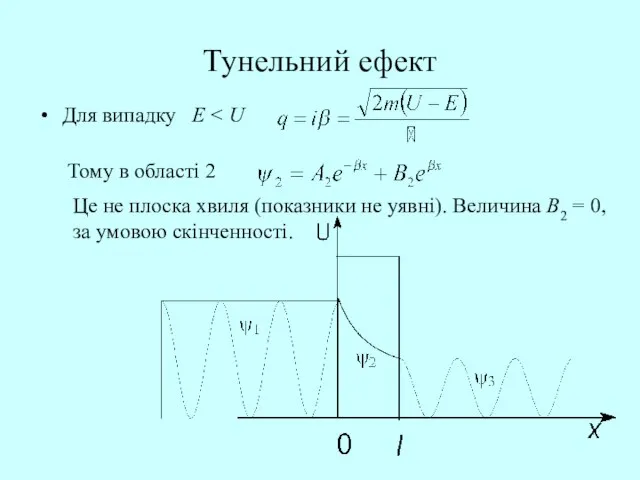
- 59. Тунельний ефект Для випадку E Тому в області 2 Це не плоска хвиля (показники не уявні).
- 60. Тунельний ефект Ймовірність проходження електрона через бар'єр (коефі-цієнт прозорості) дорівнює Щоб знайти величину D, необхідно використати
- 61. Тунельний ефект Тепер знайдемо D Для бар'єра довільної форми З формули випливає, що величина D залежить
- 62. Тунельний ефект Тунелювання є квантовим ефектом, який існує внаслідок співвідношення невизначеностей. Невизначеність Δр на відрізку Δх
- 64. Скачать презентацию














































 Презентация на тему Гидросфера
Презентация на тему Гидросфера БАНКИЗАЦИЯ РОССИИ И ЭКОНОМИЧЕСКИЙ РОСТ
БАНКИЗАЦИЯ РОССИИ И ЭКОНОМИЧЕСКИЙ РОСТ Марксистко-ленинская парадигма
Марксистко-ленинская парадигма Спутники планет
Спутники планет Иллюстрации к стихам Агнии Львовны Барто
Иллюстрации к стихам Агнии Львовны Барто Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Сложение и вычитание многочленов
Сложение и вычитание многочленов Lektsia_3_1_opredelenie_prochnosti_kirpicha_i_metalla_ispytania_Avtosokhranennyi_774
Lektsia_3_1_opredelenie_prochnosti_kirpicha_i_metalla_ispytania_Avtosokhranennyi_774 Тротуары по улице Первомайская
Тротуары по улице Первомайская Мы приглашаем вас в музей
Мы приглашаем вас в музей Основные направления культуры России первой половины XIX века
Основные направления культуры России первой половины XIX века Гендерная программа Всемирного банка в России
Гендерная программа Всемирного банка в России Г. Остер
Г. Остер М.А.Шолохов. Жизнь,творчество, личность
М.А.Шолохов. Жизнь,творчество, личность Алгоритм деятельности общеобразовательного учреждения в условиях введения новых образовательных стандартов основного общего об
Алгоритм деятельности общеобразовательного учреждения в условиях введения новых образовательных стандартов основного общего об Анри Картье-Брессон. Уличная фотография
Анри Картье-Брессон. Уличная фотография Консультации и Вебинары по личностному росту и Отношениям
Консультации и Вебинары по личностному росту и Отношениям Подготовка волонтерского корпуса для международного чемпионата в сфере строительства World Construction Championship
Подготовка волонтерского корпуса для международного чемпионата в сфере строительства World Construction Championship Тест по технологии 5 Класс Раздел программы: «Материаловедение»
Тест по технологии 5 Класс Раздел программы: «Материаловедение» Rice Moti. Наша ниша на рынке
Rice Moti. Наша ниша на рынке Связь справедливости взаимодействия с эмоциями участников (на примере политических выборов)
Связь справедливости взаимодействия с эмоциями участников (на примере политических выборов)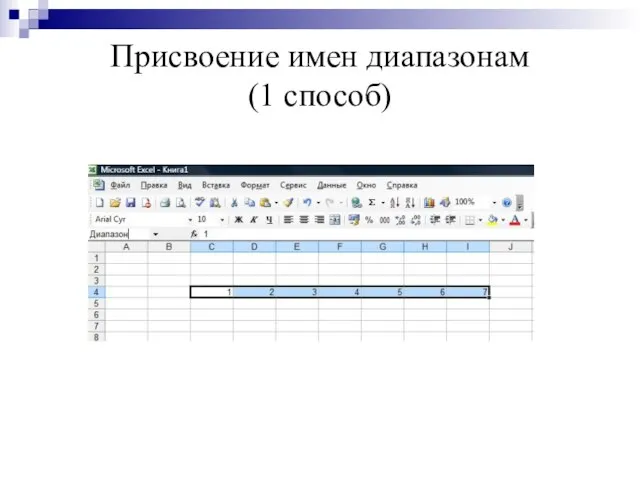 Присвоение имен диапазонам
Присвоение имен диапазонам  Пути к бесконфликтной дисциплине
Пути к бесконфликтной дисциплине Презентация на тему Первые русские князья
Презентация на тему Первые русские князья  Наркомания
Наркомания Философия науки
Философия науки Обзор технологии доступа к данным
Обзор технологии доступа к данным  Основные литературные направления
Основные литературные направления