Содержание
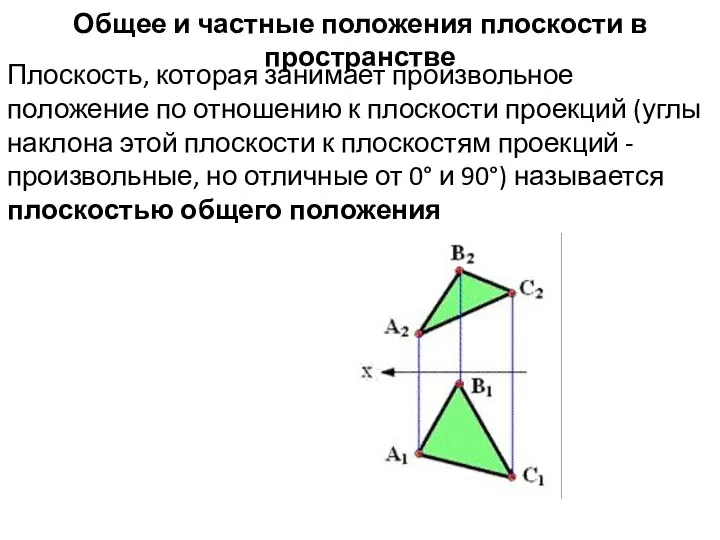
- 2. Общее и частные положения плоскости в пространстве Плоскость, которая занимает произвольное положение по отношению к плоскости
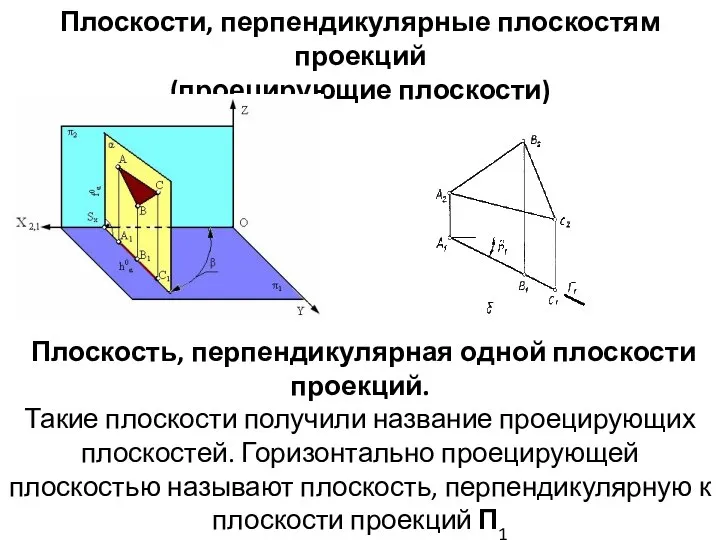
- 3. Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости) Плоскость, перпендикулярная одной плоскости проекций. Такие плоскости получили название проецирующих
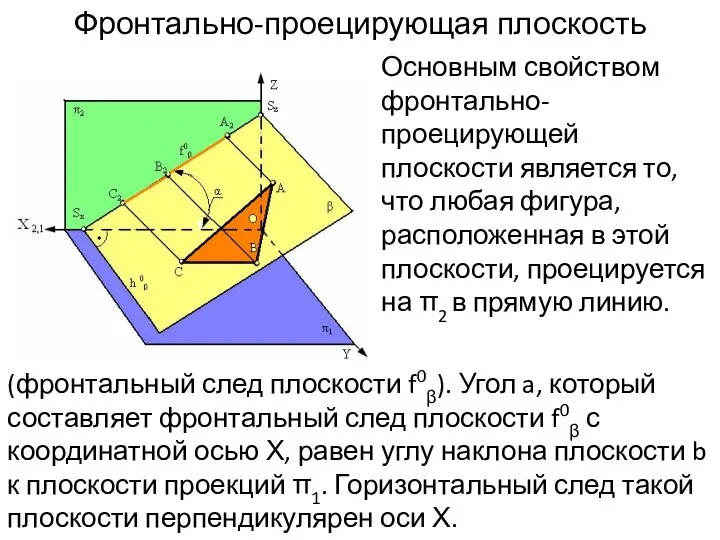
- 4. Основным свойством фронтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π2
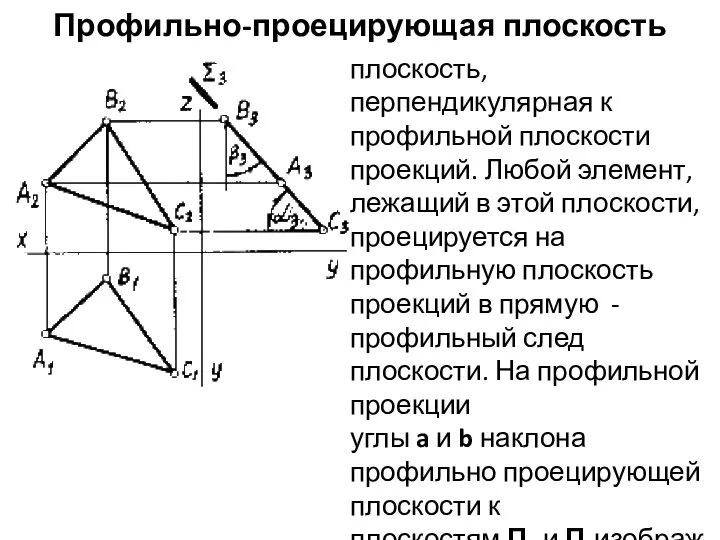
- 5. Профильно-проецирующая плоскость плоскость, перпендикулярная к профильной плоскости проекций. Любой элемент, лежащий в этой плоскости, проецируется на
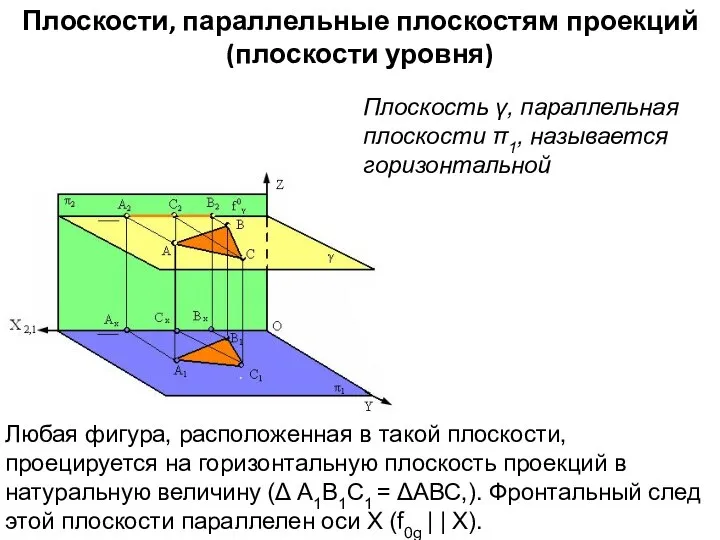
- 6. Плоскости, параллельные плоскостям проекций (плоскости уровня) Плоскость γ, параллельная плоскости π1, называется горизонтальной Любая фигура, расположенная
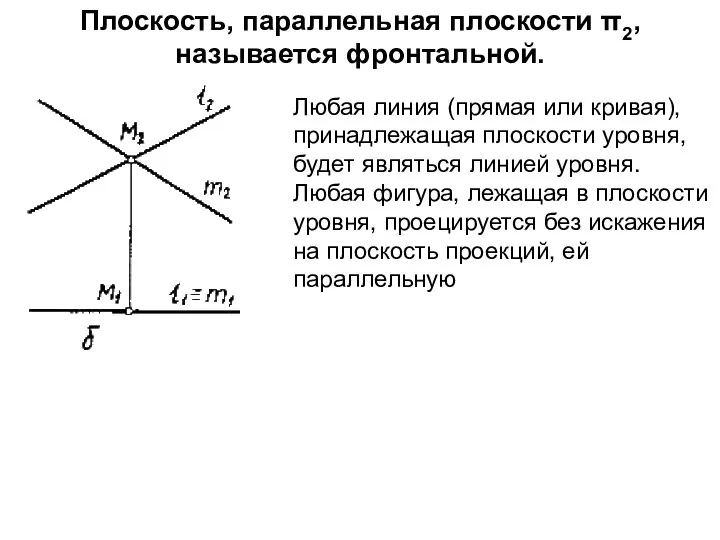
- 7. Плоскость, параллельная плоскости π2, называется фронтальной. Любая линия (прямая или кривая), принадлежащая плоскости уровня, будет являться
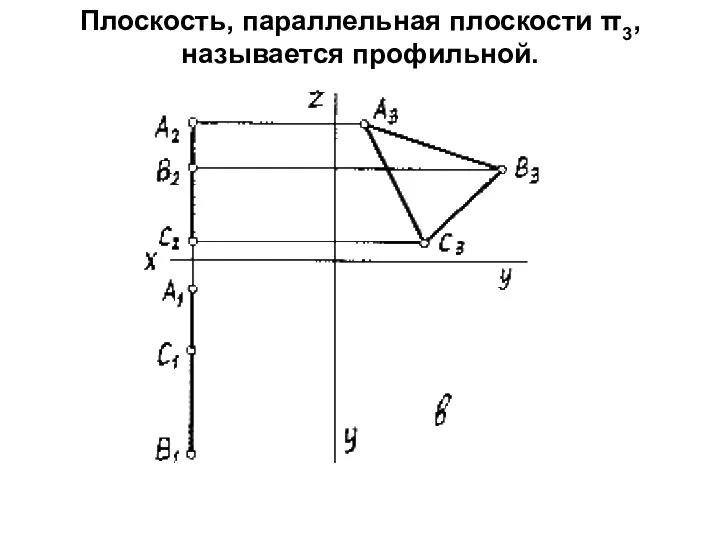
- 8. Плоскость, параллельная плоскости π3, называется профильной.
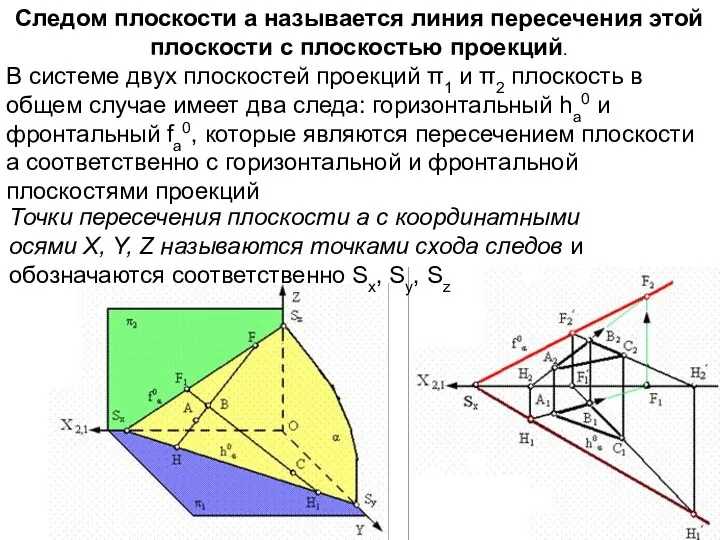
- 9. Следом плоскости a называется линия пересечения этой плоскости с плоскостью проекций. В системе двух плоскостей проекций
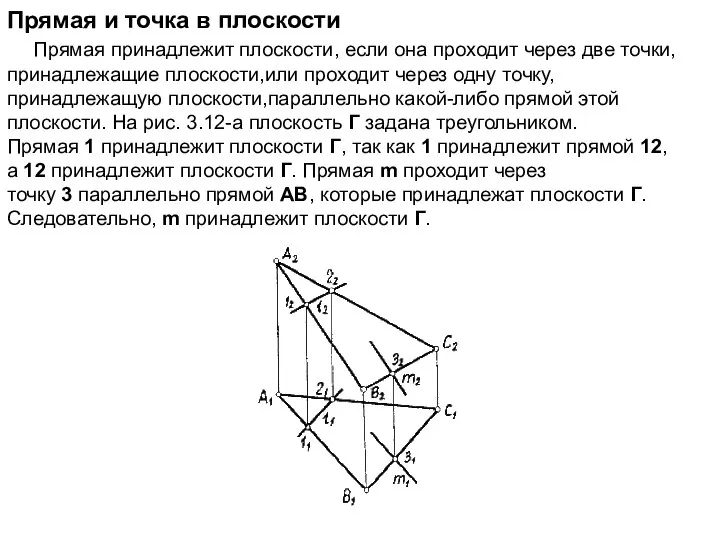
- 10. Прямая и точка в плоскости Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости,или
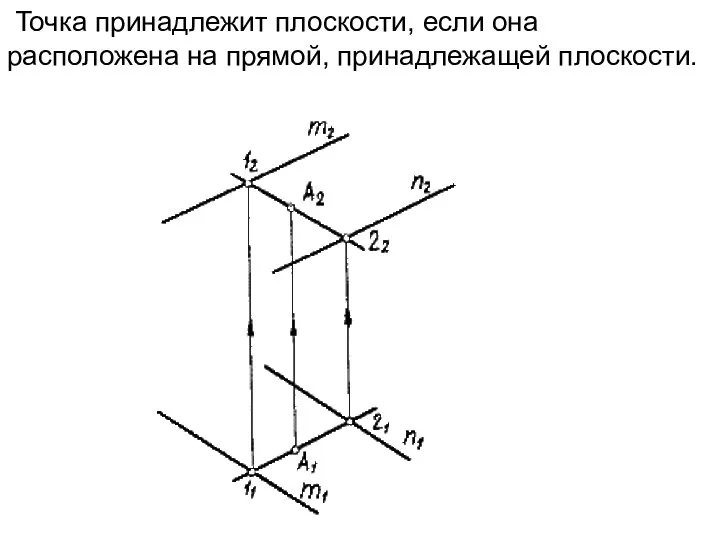
- 11. Точка принадлежит плоскости, если она расположена на прямой, принадлежащей плоскости.
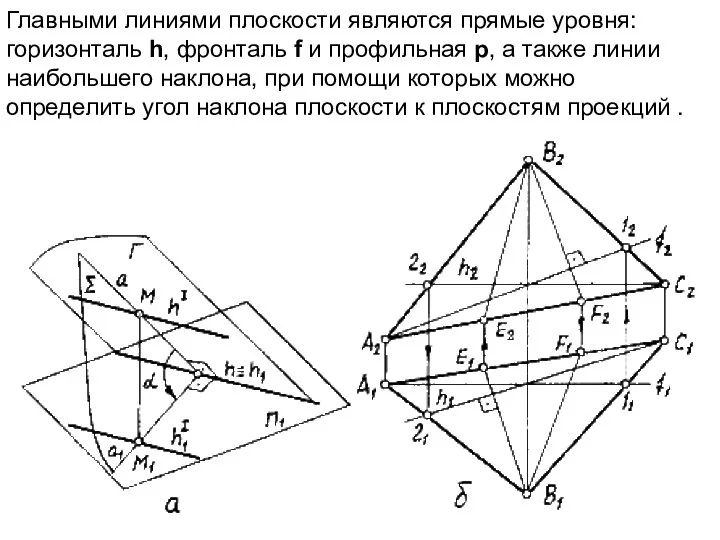
- 12. Главными линиями плоскости являются прямые уровня: горизонталь h, фронталь f и профильная р, а также линии
- 13. Линиями наибольшего наклона называют прямые данной плоскости перпендикулярные к прямым уровня этой плоскости. Прямая а наибольшего
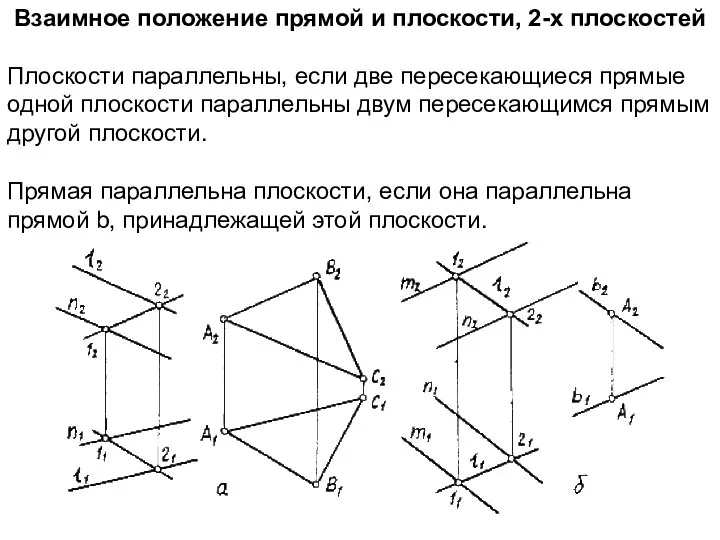
- 14. Взаимное положение прямой и плоскости, 2-х плоскостей Плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны
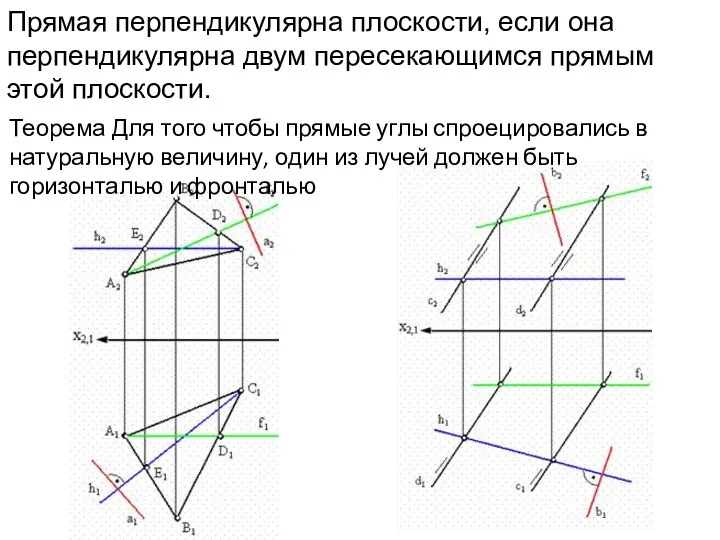
- 15. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Теорема Для того чтобы прямые
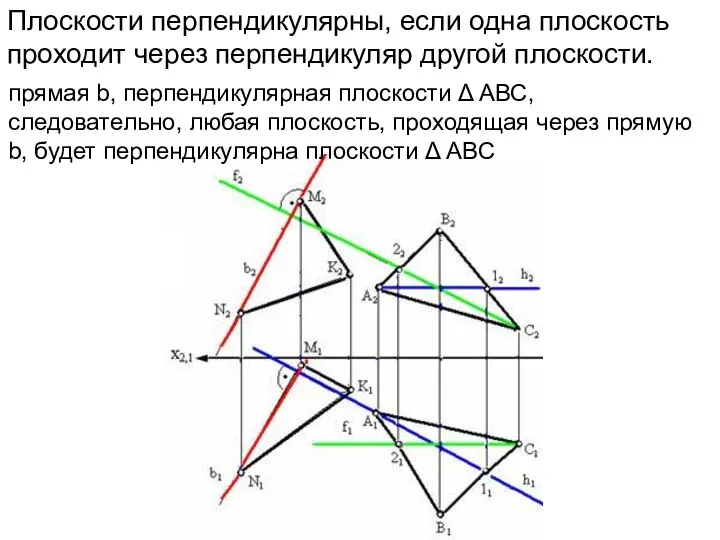
- 16. Плоскости перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости. прямая b, перпендикулярная плоскости Δ АВС,
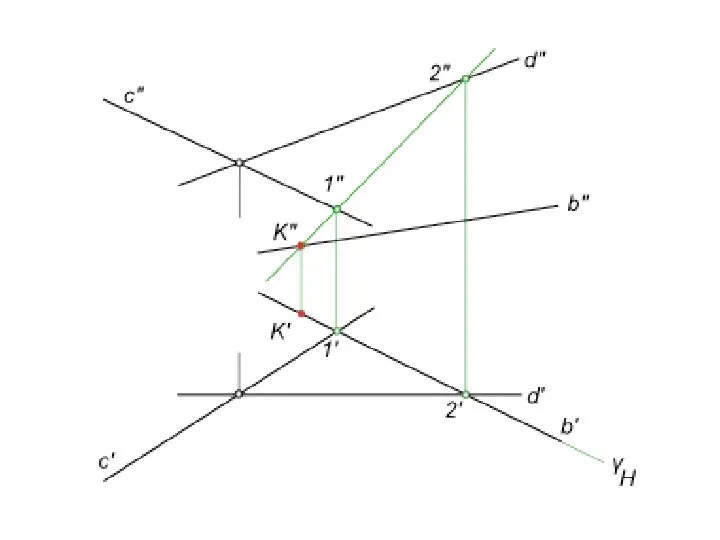
- 17. На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи : 1) проводим через b`
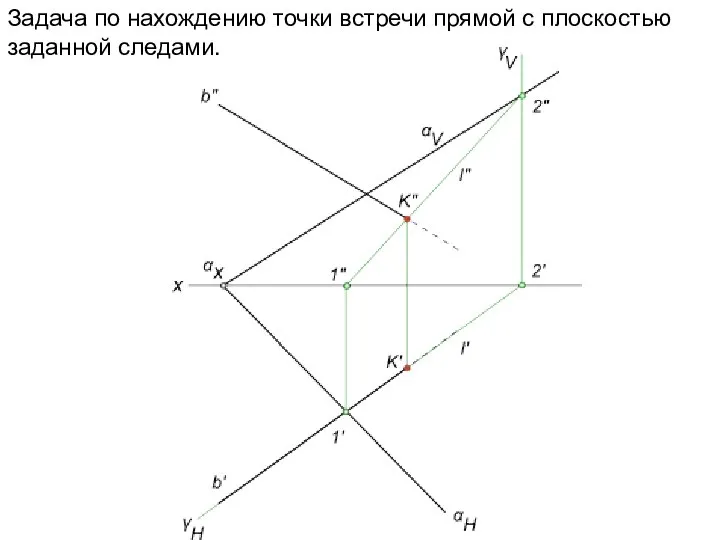
- 19. Задача по нахождению точки встречи прямой с плоскостью заданной следами.
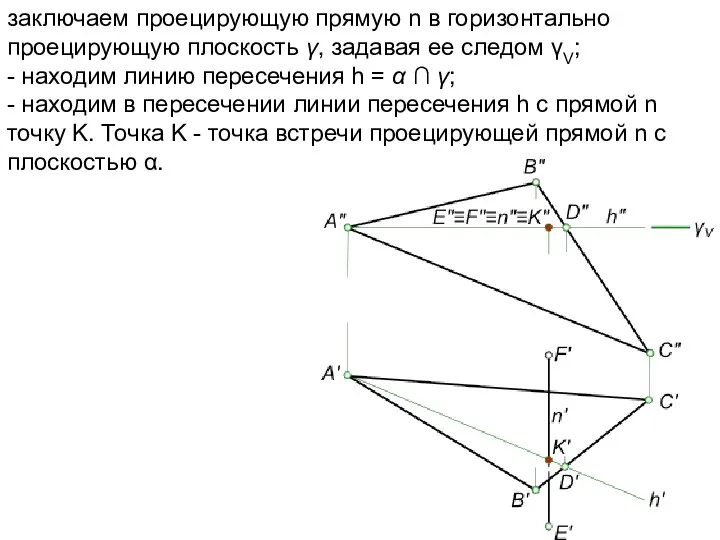
- 20. заключаем проецирующую прямую n в горизонтально проецирующую плоскость γ, задавая ее следом γV; - находим линию
- 22. Скачать презентацию


 Калевала - карело-финский поэтический эпос в обработке Элиаса Лённрота. Посёлок Калевала
Калевала - карело-финский поэтический эпос в обработке Элиаса Лённрота. Посёлок Калевала ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА «ШКОЛА 2100»
ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА «ШКОЛА 2100» Книги рекордов МТС!
Книги рекордов МТС! Комбинированный урок по географии и биологии. Разработали: Полянская Г.Н., Мелихова А.И.
Комбинированный урок по географии и биологии. Разработали: Полянская Г.Н., Мелихова А.И. Артросиндесмология
Артросиндесмология Перестраховочный рынок России
Перестраховочный рынок России Энергетика: вчера, сегодня, завтра
Энергетика: вчера, сегодня, завтра Анализ рекламных роликов
Анализ рекламных роликов ICDL международный образовательный стандарт по ИТ в Кыргызстане
ICDL международный образовательный стандарт по ИТ в Кыргызстане УПОТРЕБЛЕНИЕ ВРЕМЁН
УПОТРЕБЛЕНИЕ ВРЕМЁН Презентация на тему Второй рейх в Германии
Презентация на тему Второй рейх в Германии  ЗАВИСИМОСТЬ СКОРОСТИ ЗВУКА В ВОЗДУХЕ ОТ ЕГО СОСТОЯНИЯ
ЗАВИСИМОСТЬ СКОРОСТИ ЗВУКА В ВОЗДУХЕ ОТ ЕГО СОСТОЯНИЯ Ванны
Ванны Астероиды, метеоры, метеориты
Астероиды, метеоры, метеориты Васек Трубачев и другие
Васек Трубачев и другие Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений
Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений Бизнес–план. Модуль 3. Маркетинг. ДекорАРТ
Бизнес–план. Модуль 3. Маркетинг. ДекорАРТ Элементы литературоведческого анализа стихотворения А.С. Пушкина «И.И. Пущину»
Элементы литературоведческого анализа стихотворения А.С. Пушкина «И.И. Пущину» Первые русские храмы
Первые русские храмы Память как высшая психологическая функция
Память как высшая психологическая функция Презентация на тему Current events
Презентация на тему Current events  Великобритания
Великобритания Живописцы и скульпторы
Живописцы и скульпторы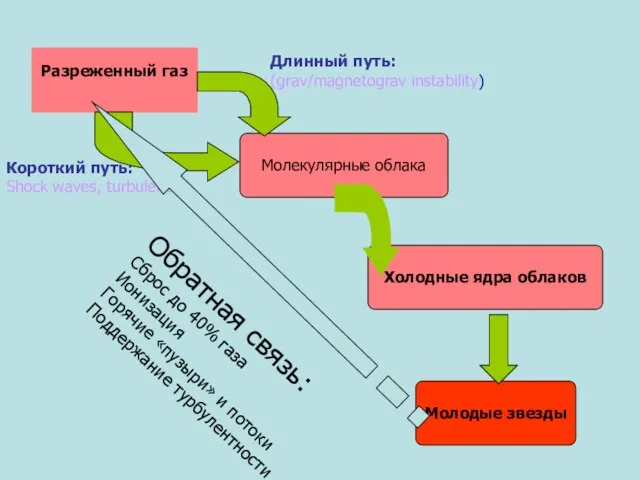 Разреженный газ Молекулярные облака Холодные ядра облаков
Разреженный газ Молекулярные облака Холодные ядра облаков Возникновение первой азбуки
Возникновение первой азбуки Право, его роль в жизни общества и государства
Право, его роль в жизни общества и государства “У каждого народа те правители, каких он заслуживает”. “У каждого народа те правители, каких он заслуживает”. историк Хилер Бэллок
“У каждого народа те правители, каких он заслуживает”. “У каждого народа те правители, каких он заслуживает”. историк Хилер Бэллок Вычисления с помощью калькулятора - презентация для начальной школы_
Вычисления с помощью калькулятора - презентация для начальной школы_