ПЛАНЕТНЫЕ КОЛЬЦА КАК РЕЛИКТЫ ПЛАЗМЕННЫХ ПРАКОЛЕЦ

Аннотация
Проводится анализ положения и структуры систем колец больших планет, основанный на решении задачи динамики и устойчивости вращающихся колец, состоявших из замагниченной плазмы. Последние рассматриваются при этом как реликты плазменных праколец. Приводятся численные оценки спектра собственных значений безразмерного параметра Ω, определяющего элитные пракольца. Теория прилагается к кольцам Юпитера, Сатурна и Урана и к плазменным торам Юпитера и Сатурна (J-тор и S-тор).

PLANETS’ RINGS
AS RELICS OF ANCIENT PLASMA RINGS
The analysis is fulfilled of great planets’ rings systems position and structure based on solution of dynamic and stability problems of the rotating magnetized plasma rings. Planets’ rings systems are considered as relics of ancient plasma rings. The numerical estimation of the non-dimensional parameters Ω eigen-values spectrum, determining the elite rings are presented. The theory has been applied to Jupiter, Saturn and Uranus rings and to the Jovian torus (Io- or J-torus) and Saturn torus (S-torus).

СОДЕРЖАНИЕ
Вводные замечания
Уравнения движения
Магнито-гравитационные волны
Магнито-гироскопические волны
Приложение к планетным кольцам
Приложение к плазменным торам
Вместо заключения
Литература

ВВОДНЫЕ ЗАМЕЧАНИЯ

Основное отличие Солнечной системы состоит, по-видимому, в том, что в прежние времена плотность плазмы, окружающей центральное тело, было гораздо выше… В результате могло реализоваться состояние частичной коротации свободно вращающейся плазмы. Строение пояса астероидов и колец Сатурна объясняется этим явлением…»
Х. Альвен

«…Устойчивость, явление принципиально общее, как-то должна, по-видимому, проявляться в законах природы». «...Квантование устойчивых орбит динамики, подобно тому, как в квантовой механике квантуются орбиты электронов. Иначе говоря, устойчивы могут быть траектории не при любых начальных данных, а лишь при некоторых, исключительных».
Н.Г. Четаев

Автор благодарен Анне Васильевне Калининой, расчеты которой подтвердили правильность главной идеи, Роберту Ефимовичу Ламперу за содействие в публикации предварительного сообщения в СибНИА им. Чаплыгина, Равилю Равильевичу Назирову за внимание и интерес к этой работе.
Автор хотел бы особо отметить творческий вклад Виктории Прохоренко в подготовку этой презентации, который трудно переоценить.

I. Уравнения движения

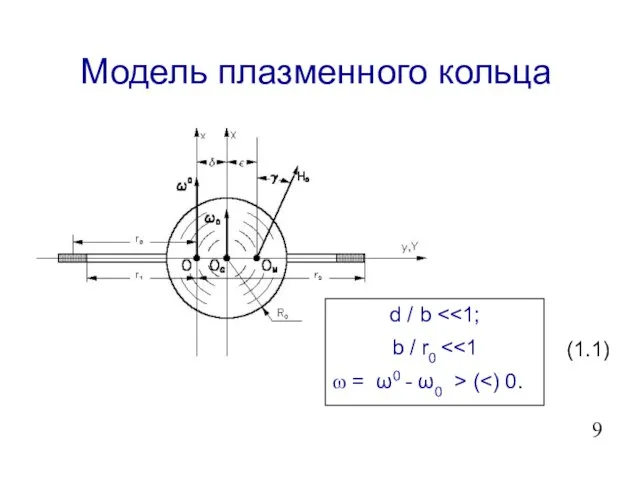
Модель плазменного кольца
d / b <<1;
b / r0 <<1
= ω0 - ω0 > (<) 0.
(1.1)

Общие уравнения
∂V/∂t + 2 (ω0×V) + 1/ρ grad p – grad U =
= (μ0 rot H×H + P)/ρ;
∂H/∂t + ω × H = rot (V×H);
div V = 0; div H = 0.
∙ V– поле скоростей;
∙ H – напряженность магнитного поля;
∙ U – потенциал поля массовых сил невозмущенного
движения (гравитационных и центробежных);
∙ ρ – массовая плотность среды;
∙ P – векторное поле внешних сил, действующих в
возмущенном движении;
(1.2)

Уравнения невозмущенного движения
A = 1 / Al = VG / a; VG = VG0 (R0 / r0)1/2 ;
A2 = A02 (r0 / R0)5; a = a0 (R0 / r0)3;
A0 = 1 / Al0 = VG0 / a0; VG0 = (g0 R0)1/2; a0 = H0 (μ0 /ρ)1/2.
VM2 = VG2 - 3a2; VM = ω0 r0.
(1.4)
(1.3)

Уравнения возмущенного движения (1)
V = V0 + v; H = H0+ h;
⏐v⏐<< ⏐VM⏐; ⏐h⏐ << ⏐H0⏐;
v = v* + v*; h = h*+ h*.
w* = grad Φ; ΔΦ = 0; v* = ∂w* /∂t;
v*= rot E; h* = rot F.
(1.5)
(1.6)

Уравнения возмущенного движения (2)
∂ rot E /∂t + 2 (ω0 × rot E) − μ0/ρ (H0,∇) rot F = 0;
rot F /∂t + (V0 , ∇) rot F − (H0,∇) rot E = -2 ∂H0/∂t;
∂ rotr E⎟Lj = 0; rotr F⎟Lj = 0, (j = 1, 2).
(1.7)
(1.8)
ΔΦ = 0; Δ(p/ρ − UΣ) = 0;
∂2∇Φ/∂t2 + 2 (ω0 × ∂∇Φ/∂t) + ∇ (p/ρ − UΣ) = 0;
∇ r (p/ρ)⎟Lj = 0, (j = 1, 2).

II. Магнито-гравитационные волны

Свободные колебания (1)
M
∑ [q″mj ∫(∇φmj, ∇φnj) dS - 2p′mj ∫(ω0x∇ϕjm, ∇φnj) dS +
m=1 S* S* + ∫(∇(p/ρ − U∑), ∇φnj) dS] = 0; n = 1, 2, …, M; j = 1,2.
S*
ϕmj(r,θ) = ρmj(r) cos mθ; φmj(r,θ) = ρmj(r) sin mθ;
ρmj(r) = Amj rm + Bmj r-m; m = 1,2,…; j = 1,2.
M
∇Φ = ∑ [pmj(t)∇ϕmj + qmj(t)∇φmj].
m=1
(2.1)
(2.2)

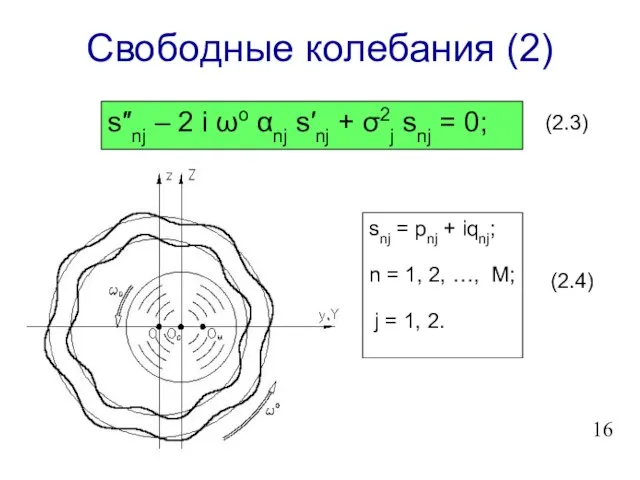
Свободные колебания (2)
s″nj – 2 i ωo αnj s′nj + σ2j snj = 0;
snj = pnj + iqnj;
n = 1, 2, …, M;
j = 1, 2.
(2.3)
(2.4)

Вынужденные колебания (1)
w∫ = ∂Φ/∂r⎟Lj = ξj0 R0 cos(θ - ωt);
h* = ix h*0 cos(θ - ωt);
ω = - ix ω; h*0 = H0 0 (R0 / r)3.
(2.5)
ξj0 = (ωj2(ε + δ) - λj2δ)/(σj2 - ω2) =
= ξj0 [(σjrj)2 +VG2(1+Al2)]/(- ω2+σj2)rj 2;
ξj0 = - δ = -3εAl2/(1 – 3 Al2).
(2.6)
σj2 = - ∂2U∑/∂r2⎟Lj = 3[(8a2 – VG2)/r2]⎟Lj;
λj2 = ∂2UG/∂r2⎟Lj = 2g0R02/r j 3;
ω j 2 = - ∂2UM/∂r2⎟Lj = 21a02R06/r8j.
(2.7)

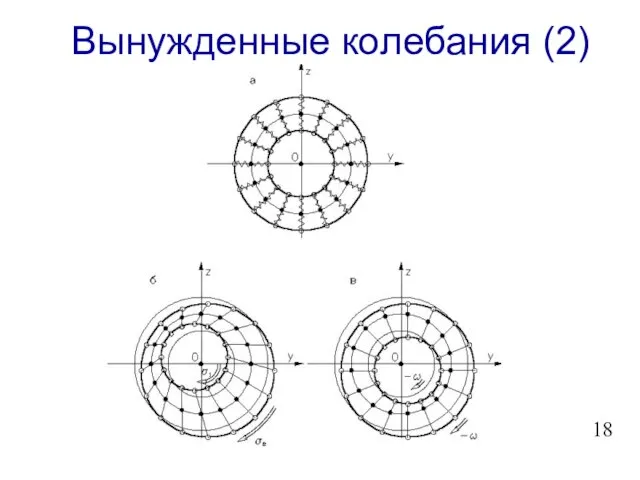
Вынужденные колебания (2)

III. Магнито-гироскопические волны

Общие уравнения
∂rot E /∂t + 2 (ω0 × rot E) − μ0/ρ (H0,∇) rot F = 0;
∂rot F /∂t + (V0,∇) rot F − (H0,∇) rot E = -2 ∂H0/∂t;
rotr E⎟Lj = 0; rotr F⎟Lj = 0, (j = 1, 2).
(3.1)
v* = rot E; h* = rot F.
(3.2)
r* = r/r0; b* = b/ro << 1; r*1 = 1 – b*/2; r*2 = 1 + b*/2;
b = r2 – r1; r1 = r*1r0; r2 = r*2r0; r0 = ½ (r1 + r2).
(3.3)

Общее решение
N
v* = ∑{αμ(t) rot [ix Cμ(r*,θ)] + γμ(t) rot [ix Sμ(r*,θ)]};
μ=1
N
h* = ∑{βμ(t) rot[ix Cμ(r*,θ)] + δμ(t) rot[ix Sμ(r*,θ)]}.
μ=1
(3.4)
Cμ(r*,θ) = sin ϕ(r*) cos μθ; Sμ(r*,θ) = sin ϕ(r*) sin μθ;
(3.5)
ϕ(r*) = π/b* (r* – 1 + b*/2),
ζμ = αμ + i γμ; χμ = βμ + i δμ.
(3.6)

Уравнения Б. Г.
νμ ζ'μ + i dμ ζμ + gμ,μ−1 e-i ω t χμ−1 + gμ,μ+1 ei ω t χμ+1 = 0;
(μ0/ρ)νμ+1χ'μ+1 - ieμ+1χμ+1 - gμ,μ−1e-i ω t ζμ - gμ+2,μ+1 ei ω t ζμ+2=0; μ = 1,3,5, …, N - 1;
gμ,μ−1 = 0 при μ = 1; gμ+2,μ+1 = 0 при μ = N – 1.
(3.7)
(μ0/ρ)νμχ'μ - i eμχμ - gμ−1,μe-i ω t ζμ-1 - gμ+1,μei ω t ζμ+1 =
= - qμ,e-iωt;
νμ+1 ζ'μ+1 + i dμ+1 ζμ+1 + gμ+1,μe-i ω t χμ + gμ+1,μ+2 ei ω t χμ+2 = 0; μ = 1,3,5, …, N - 1;
gμ-1,μ = 0 при μ = 1; gμ+1,μ+2 = 0 при μ = N – 1; qμ, = 0 при μ ≠ 1.
(3.8)

Приведение к автономной системе
ξ*μ = ζμ eiμωt; η*μ = χμ eiμωt.
(3.9)
ξμ = ξμ*/ (a0γ R 0); ημ = ημ* (μ0 ⁄ ρ)1/2 /( a0γ R 0);
= a0 γ R03 t / r04; Ω = ω r02 / (a γ r0); ω*0 = ω0 / ω.
(3.10)
ω = ω0 - ω0; a0 = H0 (μ0 / ρ)1/2; a = a0R03/ r03.
(3.11)

Уравнения автономной системы
ξ'μ + i μ Ω dμ*ξμ + g*μ,μ−1ημ-1 + g*μ,μ−1 ημ+1 = 0;
η'μ+1 − 2 i(μ + 1)Ωe*μ+1ημ+1 - g*μ,μ+1ξμ - g*μ+2,μ+1ξμ+2 = 0;
μ = 1,3,5,…, Ν − 1;
ημ−1 = 0 при μ = 1; ξμ+2 = 0 при μ = Ν − 1.
(3.12)
η'μ − 2i μ Ωe*μ ημ - g*μ-1,μ ξμ-1 - g*μ+1,μ ξμ+1 = - q*μ Ω;
ξ'μ+1 + i(μ + 1)Ωd*μ+1 ξ'μ+1 + g*μ+1,μ ημ + g*μ+1,μ+2 ημ+2 = 0, μ = 1,3,5,…, Ν − 1;
ξμ-1 = 0 при μ = 1; ημ+2 = 0 при μ = Ν − 1; q*μ = 0 при μ ≠ 1.
(3.13)

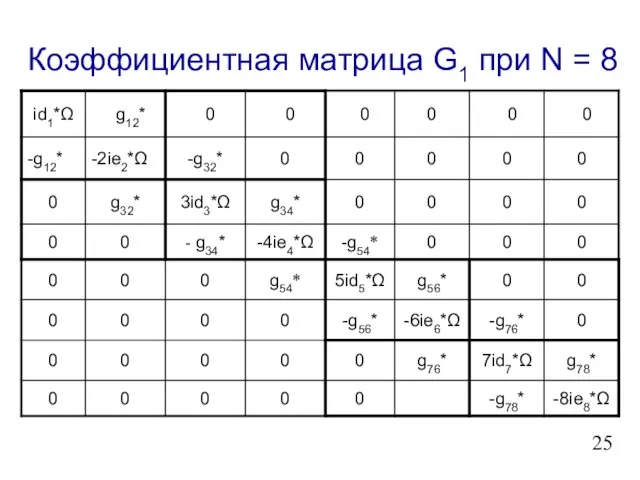
Коэффициентная матрица G1 при N = 8

Уравнения в области Лапласовых изображений.
Асимптотическое приближение
((p - iμΩ)ξμ +(μ/2) (ημ−1 − ημ+1) = pξμο;
[p − 2i(μ + 1)Ω]ημ+1 + (μ/2)ξμ − ((μ + 2)/2) ξμ+2 = pημ+1,0;
μ =1, 3, 5, …Ν−1; η0 = 0; ξΝ+1 = 0.
(3.14)
(p− 2iμΩ)ημ+ ((μ - 1)/2)ξμ−1 − ((μ +1)/2)ξμ+1 = pημ0 - q*μΩ; [p− i(μ+1)Ω]ξμ+1 + ((μ + 1)/2)(ημ − ημ+2) = pξμ+1,0;
μ = 1, 3, 5, …, Ν−1; ξ0 = 0; q*μ = 0 при μ ≠ 1.
(3.15)
gμν* = μ/2; gνμ* = μ/2 при π/b* ∞ или μ ∞.

Вынужденные колебания
− 2iμΩημ0 + ((μ - 1)/2) ξ0μ−1 − ((μ +1)/2) ξ0μ+1 = - q*μΩ;
− i(μ+1)Ωξ0μ+1 + ((μ + 1)/2)(η0μ − η0μ+2) = 0;
= 1, 3, 5, …, Ν − 1;
ξ00 = 0; η0N+1 = 0; q*μ = 0 при μ ≠ 1.
(3.16)
-2iΩη10 – ξ20 = - q1Ω;
-2iΩ ξ20 + η10 = 0.
(3.17)

Элитные значения параметра Ω (1)
ζμ = ζ*μ e -iμωt; χμ = η*μ e -iμωt;
ζ*μ = a0γR0ξμ; η*μ = a0γR0(μ0/ρ)-1/2ημ;
ζμ(nm) = const = ζμο (nm); χμ (nm) = const = χμο(nm).
mλnm = 2π rnm.
ξμ = ξμο eiστ ; ημ = ημο eiστ ;
σ = (σ*r0)/(γa) = (σ*r04)/(γa0R03);
σnm - mΩnm = 0.
(3.18)
(3.19)
(3.20)
(3.21)

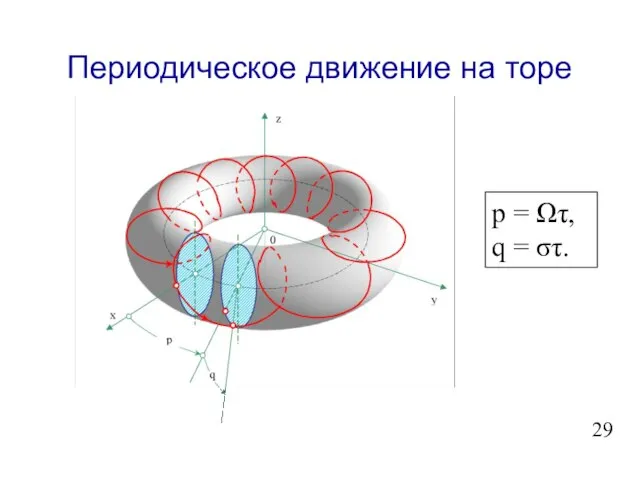
Периодическое движение на торе
p = Ωτ,
q = στ.

Учет диссипативных сил
νμ ζ'μ + i dμ ζμ + +
+ gμ,μ−1 e-i ω t χμ−1 + gμ,μ+1 ei ω t χμ+1 = 0;
(μ0/ρ)νμ+1 χ'μ+1- ieμ+1χμ+1 + -
- gμ,μ−1 e-i ω tζμ - gμ+2,μ+1 ei ω t ζμ+2 = 0.
(3.7a)

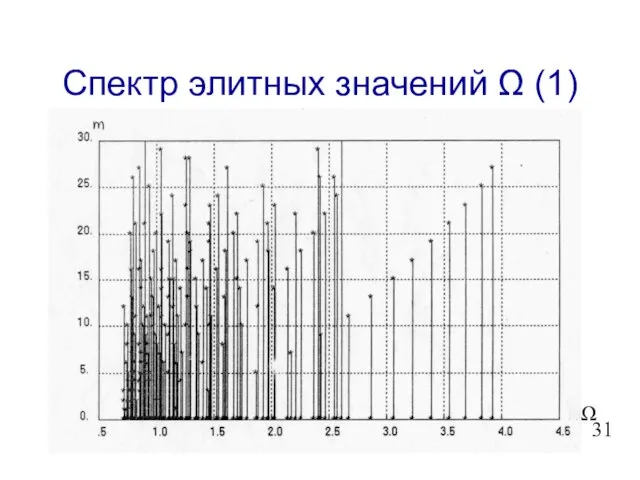
Спектр элитных значений Ω (1)
Ω

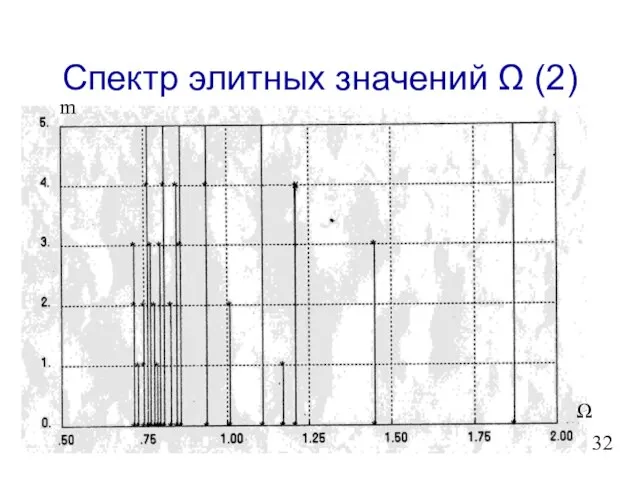
Спектр элитных значений Ω (2)
Ω
m

Аналитическое выражение для спектра критических значений Ω
det⎟Gj⎟ = 0; j = 1, 2;
[(μ+2)/(μ+1)]ημ+3 – 2(λ2+1) ημ+1 + [μ/(μ+1)] ημ-1 = 0;
μ = 1, 3, …, N – 1; η0 = 0; ηN+2 = 0.
zk+2 - 2 ch α zk+1 + zk = 0; ch α = λ2 + 1
k = 0, 1, 2,…, K – 1; K = N/2; z0 = 0; zK+1 = 0.
Ωs = 2-1/2 sin (πs / 2(Κ+1));
s = 1, 2, …, Κ; Κ = Ν/2.
2-3/2π / 2(Κ+1) < Ωs < 2-1/2.
(3.25)
(3.22)
(3.23)
(3.24)

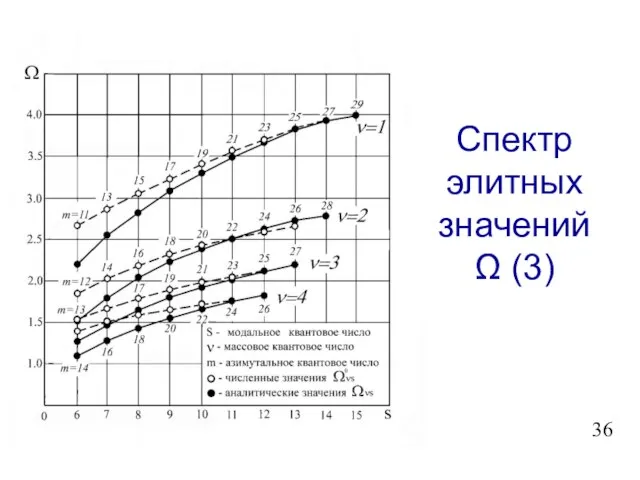
Аналитическое выражение для спектра элитных значений Ω
Ωνs = ((Κ+1)/ν)1/2 sin (πs / 2(Κ+1));
s = Κ − ν + 1, Κ−ν, Κ−ν−1, …, 1; ν = 1, 2, …, Κ;
π / 2Κ < Ωνs < (Κ+1)1/2 ; Κ = Ν/2;
⎛ 2(s - 1) + ν для (3.14)
m = ⎨
⎝ 2s - 1 + ν для (3.15)
(3.27)
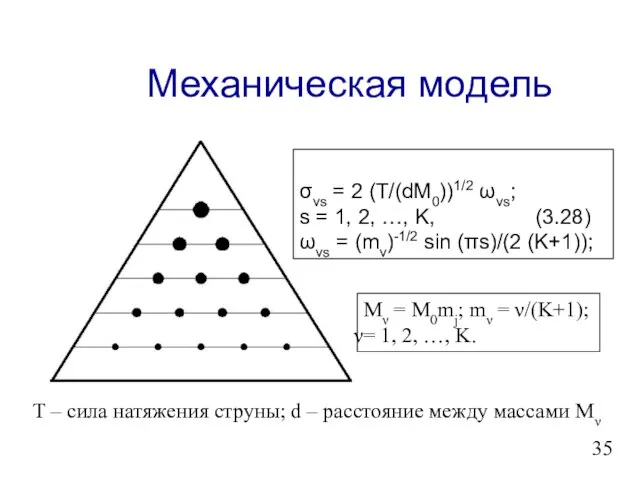
(3.26)

Механическая модель
σνs = 2 (Τ/(dΜ0))1/2 ωνs;
s = 1, 2, …, Κ, (3.28)
ωνs = (mν)-1/2 sin (πs)/(2 (Κ+1));
Mν = M0mj; mν = ν/(K+1);
= 1, 2, …, K.
T – сила натяжения струны; d – расстояние между массами Mν

Спектр элитных значений Ω (3)

Целые квантовые числа и уравнение Шредингера
Ωνkn = (n/ν)1/2 sin (πk / 2n);
k = 0, ± 1, ± 2, …, ± l; l = 1, 2, …;
n = l + ν; ν = 1, 2 ….
(3.29)
(3.30)
В решении уравнения Шредингера, соответствующем атому водорода, числа n, l, k совпадают со следующими квантовыми числами:
«Главным квантовым числом" n,
«Квантовым числом полного кинетического момента" l,
«Магнитным квантовым числом" k.
n = K + 1;
l = K + 1 - ν;
k = 0, ± s.

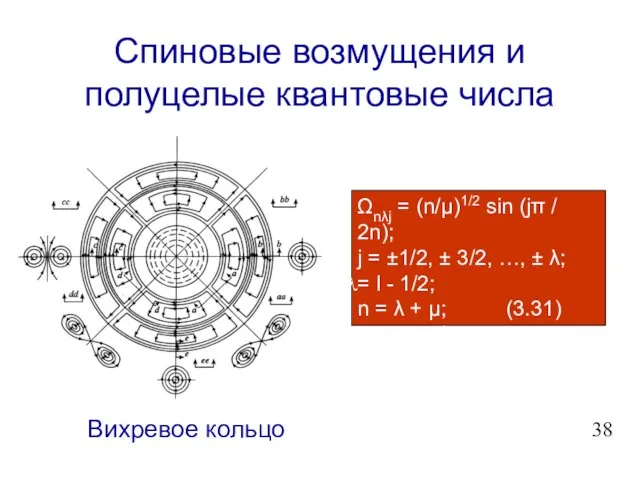
Спиновые возмущения и полуцелые квантовые числа
Ωnλj = (n/μ)1/2 sin (jπ / 2n);
j = ±1/2, ± 3/2, …, ± λ;
= l - 1/2;
n = λ + μ; (3.31)
μ = ν + ½.
Вихревое кольцо

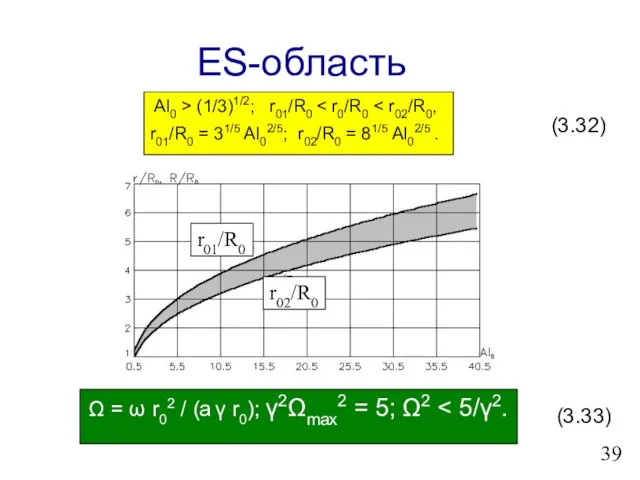
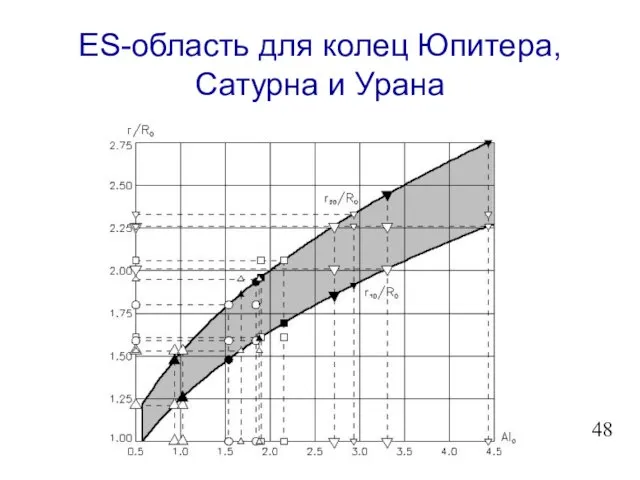
ES-область
Al0 > (1/3)1/2; r01/R0 < r0/R0 < r02/R0,
r01/R0 = 31/5 Al02/5; r02/R0 = 81/5 Al02/5 .
Ω = ω r02 / (a γ r0); γ2Ωmax2 = 5; Ω2 < 5/γ2.
(3.32)
(3.33)
r01/R0
r02/R0

IV. Приложение к планетным кольцам

Системы колец Сатурна и Урана
Кольца Сатурна (Cassini)
Кольца Урана (Voyager 2)
Кольца Сатурна: Фрагмент кольца А (Cassini); Кольца B и C (Voyager 2)

Voyager и кольца Сатурна (1)
Руководитель группы отображения миссий Voyager Брэд Смит:
«Сотни неожиданных колечек внутри колец появляются перед электронными глазами `Вояджера`. Деление Кассини, предположительно свободная зона между внешним кольцом А и средним кольцом В, ожила, по меньшей мере, тремя дюжинами малых колечек. Удивительные спицы протянулись в радиальном направлении поперек кольца В».
«Большинство астрономов полагают, что с тех пор как кольца еще формировались, этот процесс всегда является рутинным следствием законов небесной механики, особенно - механизма, называемого резонансом. До Вояджера такие резонансы предполагались ответственными за те локальные структуры, которые демонстрируют кольца. Но теперь мониторы JPL (Jet Propulsion Laboratory) видят больше структур не только в кольцах, но и в делении Кассини, чем может объяснить любая симфония резонансов».

Voyager и кольца Сатурна (2)
«Мы думали, что увидели все, что можно было увидеть, но в этом странном мире колец Сатурна причудливое стало банальностью; когда мы посмотрели сегодня на кольцо, вот, что мы увидели»:
То, что показал Смит, - это картина кольца F, расщепленного на три пряди, две из которых оказались переплетенными, как косы.
«'Косы' бросают вызов законам небесной механики по многим причинам, - сказал он, - но, очевидно, эти кольца ведут себя правильно (these rings are doing the right thing); я полагаю, что мы просто не очень хорошо понимаем законы…»

Cassini и кольца Сатурна
Руководитель группы отображения миссий Cassini Каролин Порко:
«Стало немедленно очевидно после изучения 61 изображения, что мы обнаружили целую коллекцию новых явлений, которые никогда не удавалось увидеть раньше, а некоторые из которых даже предвидеть.
Мы видели много узких колечек, отделенных от широких лент, разрезанных на множество казавшихся некогерентными структур.
Но по большей части мы видели волны, много волн…»
«Волны являются точно идентифицируемыми, но странными структурами, и мы не имеем сколько-нибудь полного удовлетворительного объяснения того, почему они выглядят именно так. Соответствующие теории `спотыкались` много лет тому назад, когда отсутствовали достаточно точные данные, на которых они могли бы базироваться. Сейчас, вернувшись к Сатурну, мы имеем щедрую информацию, которая, конечно, будет стимулировать изучение формирования и распространения этих волн…»
Гамлет: «И в небе и в земле сокрыто больше, чем снится вашей мудрости, Горацио»

Гипотеза о стратификации эволюционно зрелого плазменного пракольца
Эволюционно зрелое вращающееся пракольцо, состоящее из замагниченной плазмы, оказывается расщепившееся на большое количество элитных колец, определяемых элитными собственными значениями фундаментального безразмерного параметра Ω.
Дальнейшая стратификация пракольца и наличие дополнительных возмущений приводит к появлению уплотнений, становящихся центрами аккреции. В этих центрах начинают формироваться, благодаря известному механизму гравитационной неустойчивости, твердые частицы, что, в конечном счете, приводит к картине наблюдаемой сейчас.
С этой точки зрения современные планетные кольца представляют собой реликты наиболее "жизнеспособных", эволюционно зрелых плазменных праколец.

Эволюция элитных колец

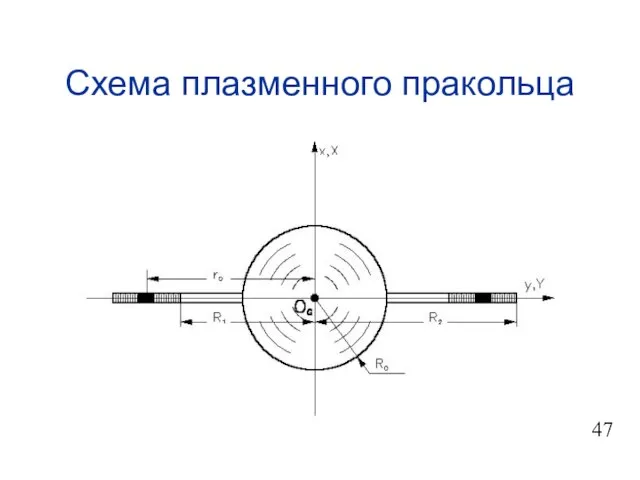
Схема плазменного пракольца

ES-область для колец Юпитера, Сатурна и Урана

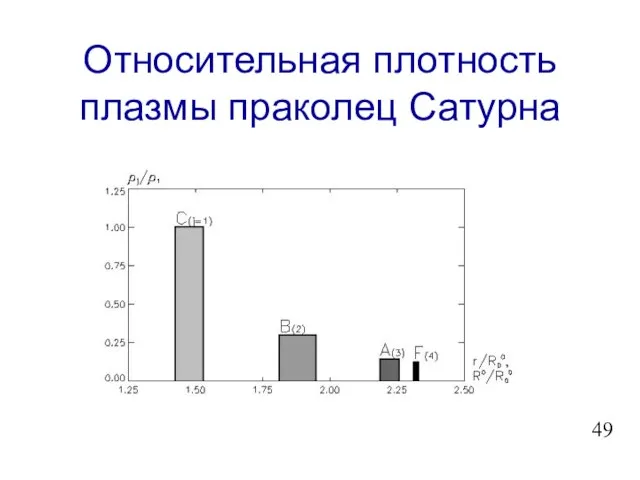
Относительная плотность плазмы праколец Сатурна

V. Приложение к планетным торам

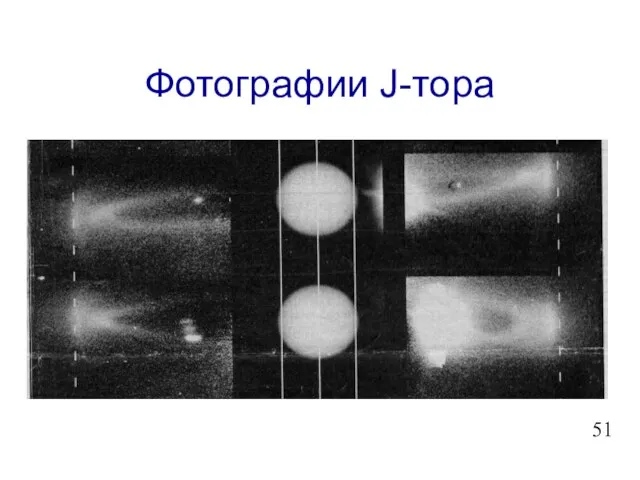
Фотографии J-тора

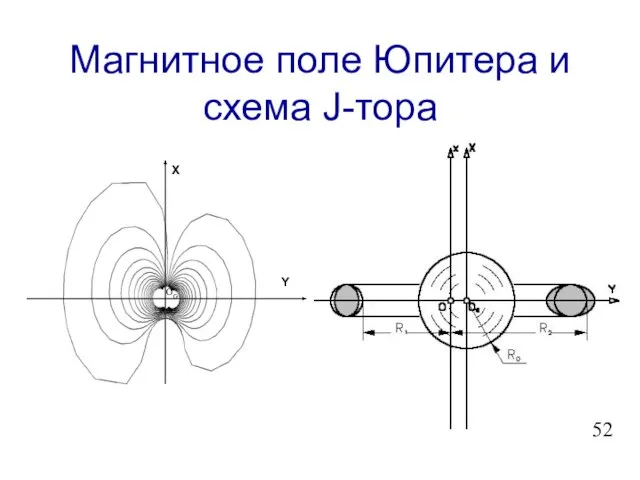
Магнитное поле Юпитера и схема J-тора
X
Y
OG

Может ли существовать J-тор?
Мнение компетентных специалистов
«Этот тор является динамически неустойчивым (?!), поскольку направленная к периферии центробежная сила, обусловленная коротацией, значительно превосходит направленную к центру гравитационную силу Юпитера. Эта неустойчивость создает отток плазмы из тора, что должно, в конечном счете, приводить к ее ускользанию в магнитосферу планеты. И хотя такой отток является неизбежным, детальная природа его неизвестна и поэтому является предметом активного обсуждения. Результаты наблюдений, проведенных космическим аппаратом Galileo, возможно, внесут ясность в этот вопрос».
Hill, T.W. and A.J. Dessler. Space Physics and Astronomy Converge in Exploration of Jupiter's Magnetosphere // EOS Trans. AGU. 76. № 33. 1995. P. 313-314.
Скорее нет, чем да. Судите сами:

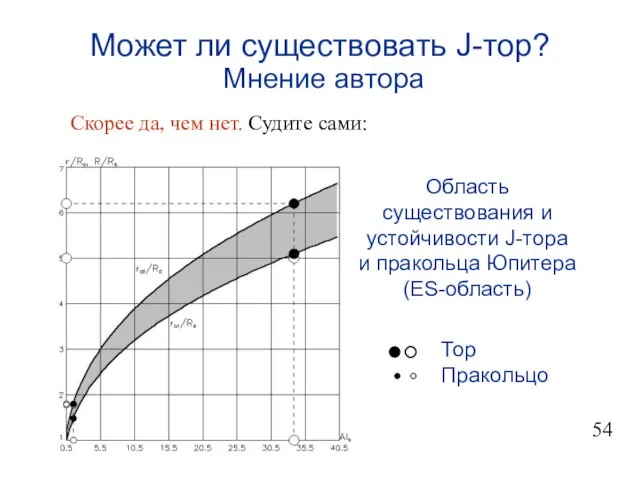
Может ли существовать J-тор?
Мнение автора
Скорее да, чем нет. Судите сами:
Область существования и устойчивости J-тора
и пракольца Юпитера (ES-область)
Тор
Пракольцо

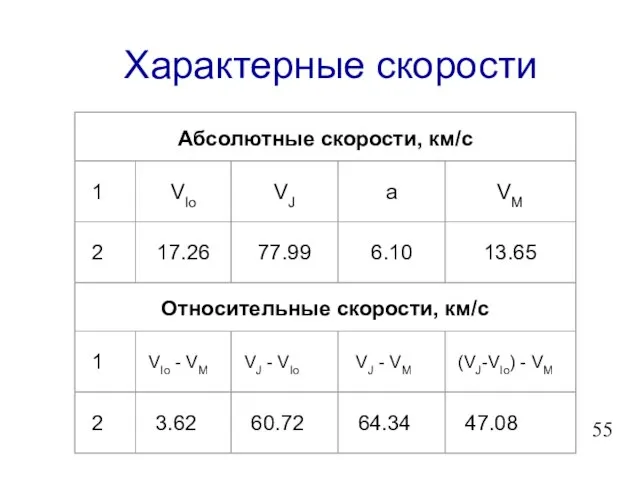
Характерные скорости

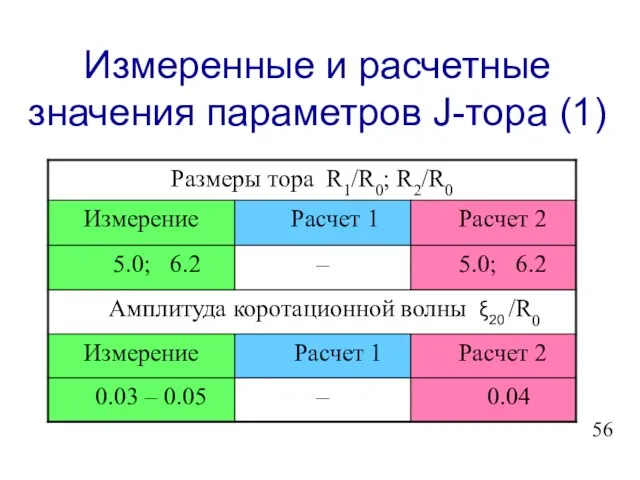
Измеренные и расчетные значения параметров J-тора (1)

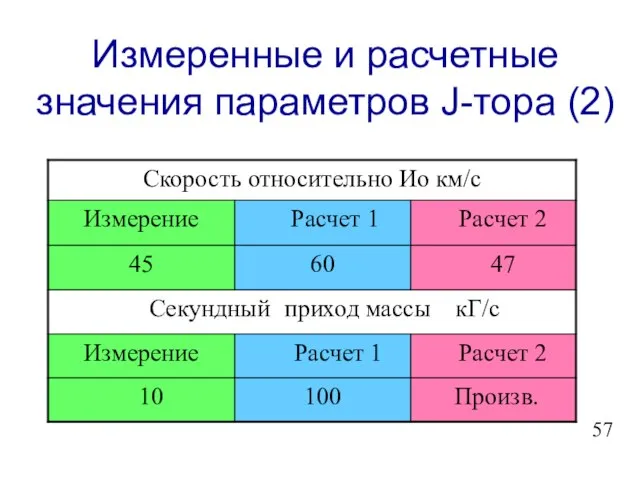
Измеренные и расчетные значения параметров J-тора (2)

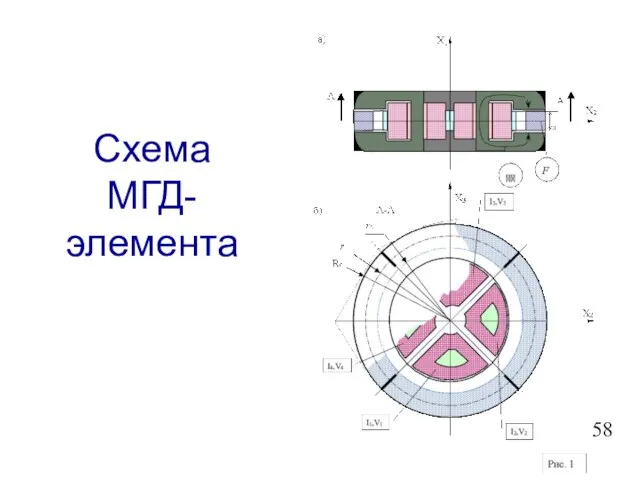
Схема МГД-элемента

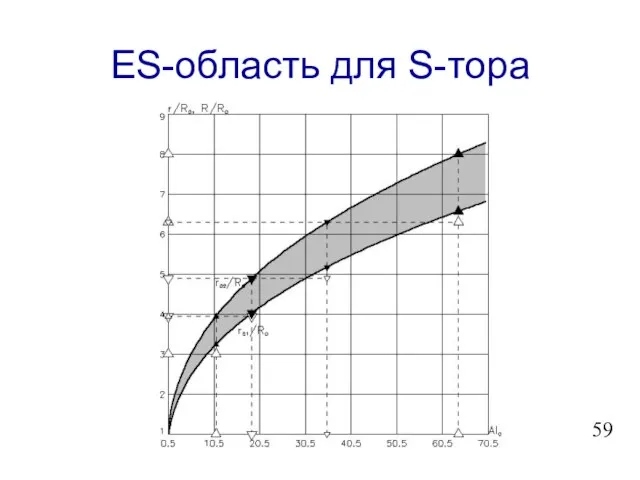
ES-область для S-тора

ВМЕСТО ЗАКЛЮЧЕНИЯ
Вернемся в заключение к проблеме превращения совокупности плазменных элитных колец, на которые расщепилось эволюционно зрелое пракольцо, в систему колец, наблюдаемых у каждой из больших планет, состоящее из твердых элементов. Возникает принципиальный вопрос, заключающийся в следующем. Как получилось, что элитные кольца не только «запомнили» до мельчайших деталей свою конфигурацию в момент «рождения», но и сумели сохранить ее до наших дней?

Ответ на этот вопрос, по-видимому, дает теорема В.И. Арнольда о вековой устойчивости Солнечной системы. Каждое из элитных плазменных колец превратилось в процессе эволюции в соответствии с гипотезой, сформулированной выше, в пылевое кольцо, состоящее из твердых частиц. В дальнейшем частицы все больше укрупнялись благодаря гравитационной неустойчивости. Однако каждое элитное кольцо сохранило при этом свою индивидуальность и заняло определенное место в пространстве. В конечном счете, сформировалась система многочисленных узких колечек, состоящих из твердых элементов. Эти элементы должны неограниченно долго существовать на тех орбитах, на которых они «родились», за исключением тех орбит, которые были скорректированы за счет резонансных эффектов.