LinAl_Lektsia_2

Определитель матрицы
Квадратные матрицы. Степень матрицы. Многочлен от матрицы.
Система линейных уравнений. Случай n=2.
Определитель матрицы.
Определение определителя.
Разложение Лапласа по строкам и столбцам.
Основные свойства определителя.
Определитель и элементарные операции.
Задачи.

Несколько слов о квадратных матрицах

О перестановке в двух словах

О перестановке в двух словах

Перестановка для матриц

Для чего нужен определитель квадратной матрицы? Как он определяется? А как же он вычисляется?

Система лин. уравнений

Система с двумя переменными, n=2

Продолжение

Для случая n=3.

Минор и алгебраическое дополнение матрицы

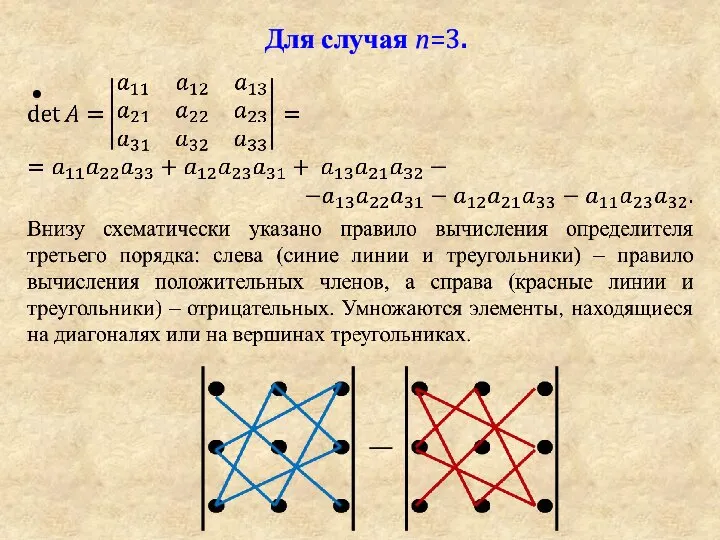
Все-таки, как вычислить определитель для любого n

Пример вычисления определителя

Основные свойства определителя

Основные свойства определителя

Основные свойства определителя

Другие свойства определителя

Основные свойства определителя

Об определителе произведения двух матриц

Об определителе произведения двух матриц

Свойства определителя

Примеры вычисления определителей спец. вида
Следующая матрица называется нижней треугольной.

Примеры вычисления определителей спец. вида

Некоторые примеры
1.
a

Пример
Доказать, что
1

Пример
Доказать, что

Задание 2

Задачи 2
3) Согласно определению, определитель равен сумме n! членов, составлена следующим образом: 1) членами служат всевозможные произведение n элементов матрицы, взятых по одному в каждой строке и в каждом столбце; 2) знак произведения зависит от четности перестановки (см. слайды данной лекции). Пользуясь только первым условием вычислить следующие определители.
[их]
4) Вычислить определитель:

Задача 2
5) Пусть для матрицы X выполняется условие
Найти det X.
6)

Задачи
7) Вычислить определитель
8) [dem] Вычислить определитель порядка n, приведением их к треугольной форме