Содержание
- 2. Цели урока: Ввести определение линейного уравнения с двумя переменными; решения линейного уравнения с двумя переменными; разобрать
- 3. Равенство, содержащее две переменные, называется уравнением с двумя переменными. Линейным уравнением с двумя переменными называется уравнение
- 4. Определение: решением уравнения с двумя переменными называется пара значений переменных, которые обращают это уравнение в верное
- 5. Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной. 1.Если в
- 6. Например, а) Уравнения Равносильны, так как член перенесен (с изменением знака) из левой части в правую.
- 7. Алгоритм доказательства, что данная пара чисел является решением уравнения: 1)записать данное уравнение; 2) подставить в уравнение
- 8. Попробуй сам: № 1092, является ли данное уравнение линейным, если да назови его коэффициенты; №1094, устно;
- 9. Итог урока: -Что называется уравнением с двумя переменными? Приведите примеры. -Какое уравнение с двумя переменными называется
- 11. Скачать презентацию








 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр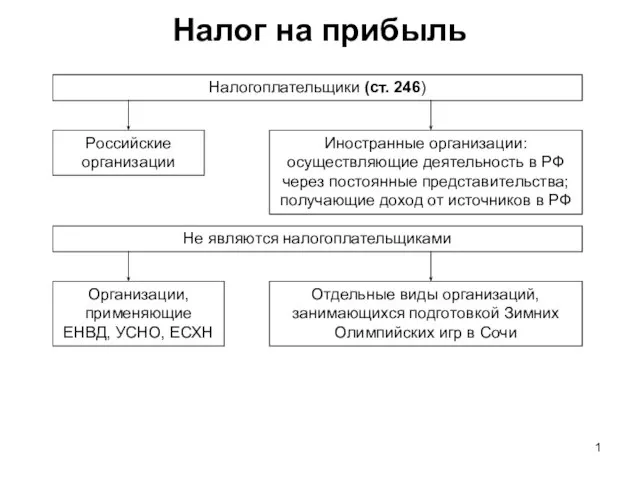 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология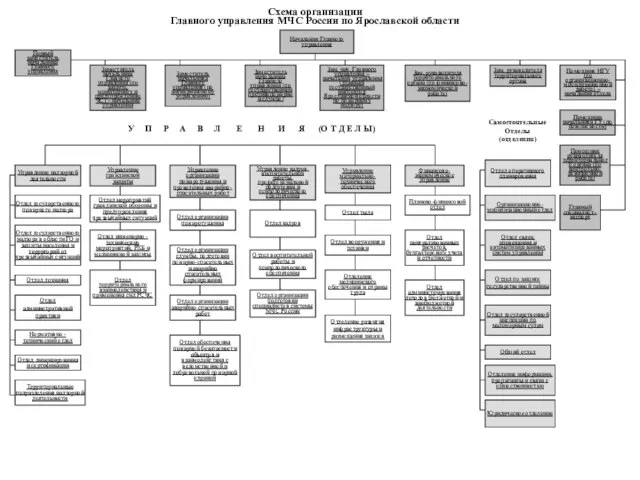 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва