Содержание
- 2. 2 3 4 5 6 7 8
- 3. 2 3 1
- 4. 2 3 4 5 6 7 8
- 16. Пример. М – множество решений системы линейных однородных уравнений с n неизвестными. Покажем, что М –
- 20. Теорема 4.1. Существует взаимно однозначное соответствие между множеством линейных операторов n-мерного линейного пространства и множеством квадратных
- 29. Замечания. 1) 2) 3)
- 30. Определение. Вещественное линейное пространство, в котором определено скалярное произведение векторов, называется евклидовым. E(n)
- 31. Процесс ортогонализации векторов Грама – Шмидта
- 34. ,
- 35. . .
- 36. .
- 37. , . .
- 38. .
- 41. Скачать презентацию






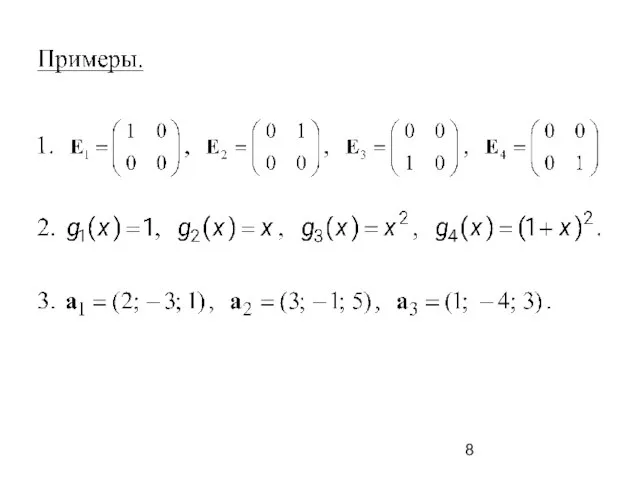




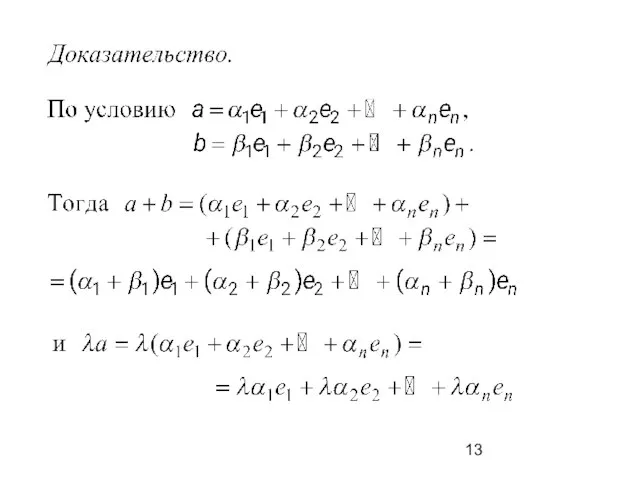








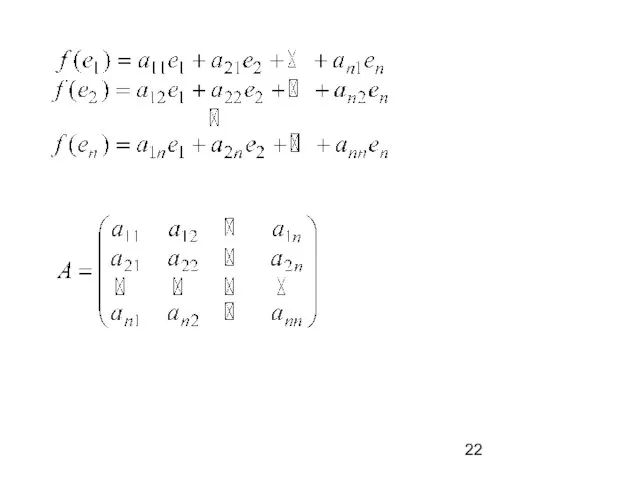

















 Показатели качества деталей. Классификация показателей качества продукции. Определение номеклатуры показателей качества
Показатели качества деталей. Классификация показателей качества продукции. Определение номеклатуры показателей качества Кожа и ультрафиолетовые лучи
Кожа и ультрафиолетовые лучи Принципы, критерии и методы педагогического прогнозирования индивидуальной образовательной траектории
Принципы, критерии и методы педагогического прогнозирования индивидуальной образовательной траектории Студенческое самоуправление:основные мероприятия в 2011 г.
Студенческое самоуправление:основные мероприятия в 2011 г. Игры со шнуровкой
Игры со шнуровкой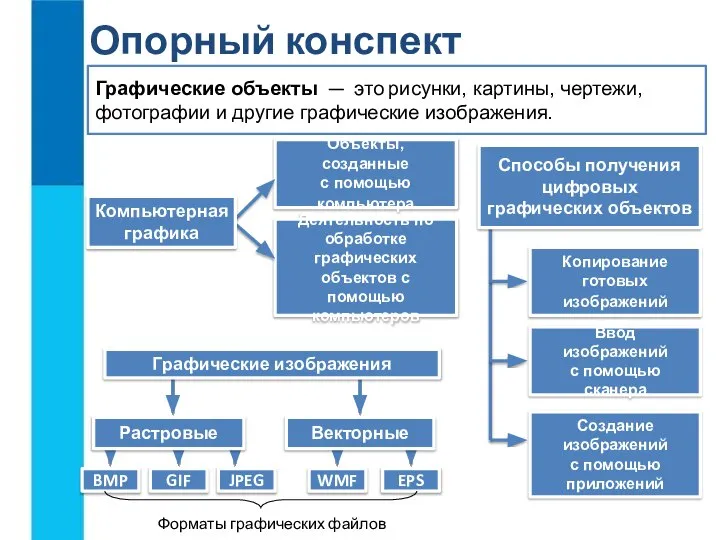 Графические объекты. Опорный конспект
Графические объекты. Опорный конспект Жизнь экосистемы. Биосфера и экосистема. Экологическая система
Жизнь экосистемы. Биосфера и экосистема. Экологическая система Руководство механики работы по проекту AUTO.RU
Руководство механики работы по проекту AUTO.RU Особенности энергосервисных контрактов в многоквартирных домах
Особенности энергосервисных контрактов в многоквартирных домах Презентация на тему Умножение и деление положительных и отрицательных чисел
Презентация на тему Умножение и деление положительных и отрицательных чисел Популяция (1)
Популяция (1) Конкурсный проект смотровой площадки на вершине горы Машук
Конкурсный проект смотровой площадки на вершине горы Машук Презентация на тему Рокоссовский Константин Константинович
Презентация на тему Рокоссовский Константин Константинович  Радианная мера углов и дуг
Радианная мера углов и дуг ДИАГРАММА «Моя квартира»
ДИАГРАММА «Моя квартира» Инфекционные осложнения после абортов
Инфекционные осложнения после абортов Гонка Чемпионов: Шумахер или Лёб? Тактика выживания бизнеса в кризис Сергей Петренко 1 апреля 2009 года. - презентация
Гонка Чемпионов: Шумахер или Лёб? Тактика выживания бизнеса в кризис Сергей Петренко 1 апреля 2009 года. - презентация Сведения о бетоне
Сведения о бетоне Право и государство
Право и государство За счет чего российские компании могут конкурировать глобально?
За счет чего российские компании могут конкурировать глобально? Cистема FATC1 климат-контроль
Cистема FATC1 климат-контроль "АНТИКРИЗИСНОЕ УПРАВЛЕНИЕ"
"АНТИКРИЗИСНОЕ УПРАВЛЕНИЕ" Александр Невский (7 класс)
Александр Невский (7 класс) Фонд обязательного медицинского страхования
Фонд обязательного медицинского страхования Ясенев Вячеслав Николаевич
Ясенев Вячеслав Николаевич Летний оздоровительный лагерь «МАЛЫШОК»
Летний оздоровительный лагерь «МАЛЫШОК» Программы сопровождения педагогических кадров Профессионал
Программы сопровождения педагогических кадров Профессионал Презентация на тему Антикоррупционная политика
Презентация на тему Антикоррупционная политика