Содержание
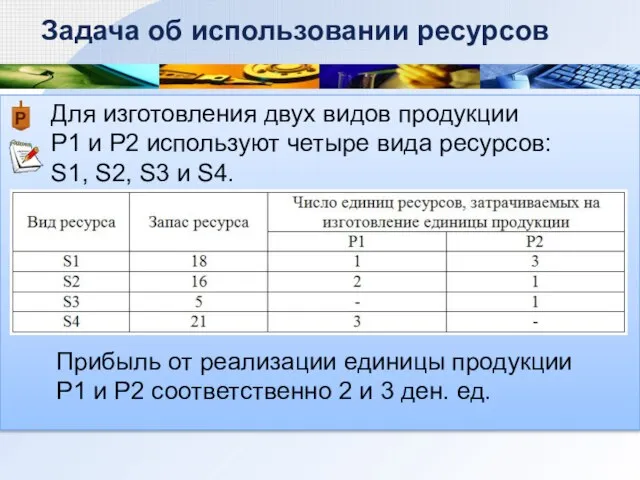
- 2. Для изготовления двух видов продукции Р1 и Р2 используют четыре вида ресурсов: S1, S2, S3 и
- 3. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной Задача об
- 4. Решение Введем переменные Задача об использовании ресурсов Х1 – число единиц продукции Р1, запланированных к производству
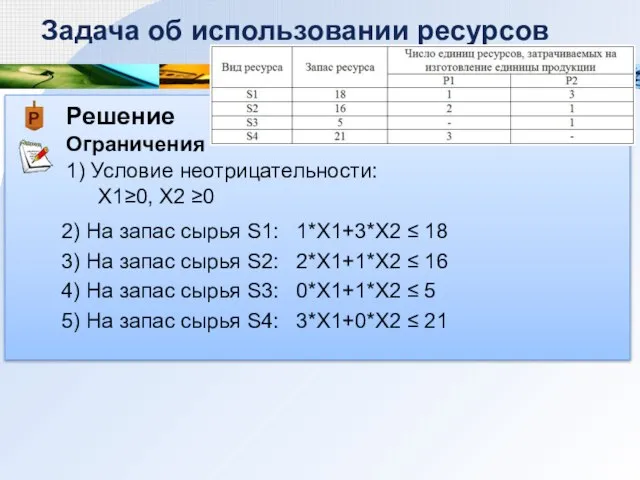
- 5. Решение Ограничения Задача об использовании ресурсов 1) Условие неотрицательности: Х1≥0, Х2 ≥0 2) На запас сырья
- 6. Экономико-математическая модель (задача линейного программирования) Задача об использовании ресурсов
- 7. Экономико-математическая модель (коротко)
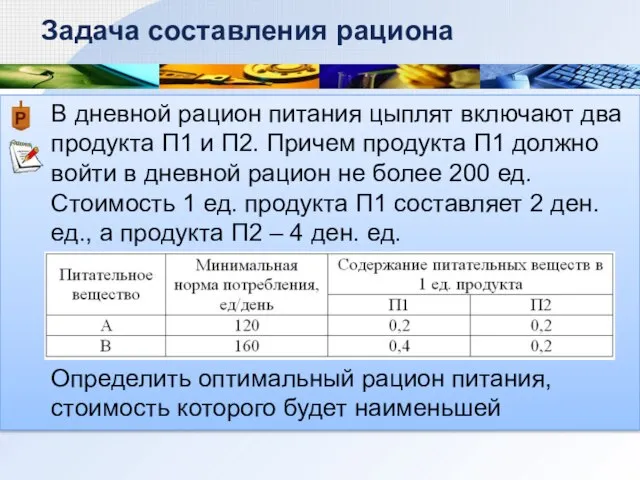
- 8. В дневной рацион питания цыплят включают два продукта П1 и П2. Причем продукта П1 должно войти
- 9. Решение Введем переменные Задача составления рациона Х1 – число единиц продукта П1, входящего в дневной рацион
- 10. Решение Ограничения Задача составления рациона 1) Условие неотрицательности: Х1≥0, Х2 ≥0 2) Ограничение на максимальное содержание
- 11. Экономико-математическая модель (задача линейного программирования) Задача составления рациона
- 12. Поясним термин линейное программирование линейное означает: ищется экстремальное значение (min или max) линейной целевой функции при
- 13. Каноническая задача линейного программирования
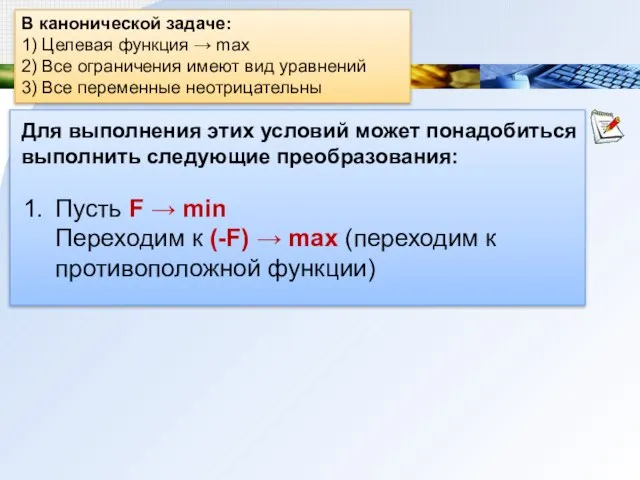
- 14. Каноническая задача линейного программирования В канонической задаче: 1) Целевая функция → max 2) Все ограничения имеют
- 15. В канонической задаче: 1) Целевая функция → max 2) Все ограничения имеют вид уравнений 3) Все
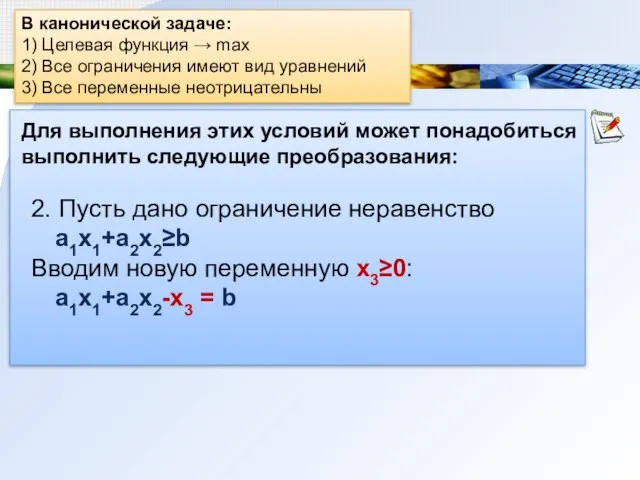
- 16. В канонической задаче: 1) Целевая функция → max 2) Все ограничения имеют вид уравнений 3) Все
- 17. В канонической задаче: 1) Целевая функция → max 2) Все ограничения имеют вид уравнений 3) Все
- 19. Скачать презентацию











 Сохраняя традиции вкуса, используя уникальные современные технологии, мы создали для Вас столовые приборы, которые сделают Вашу ж
Сохраняя традиции вкуса, используя уникальные современные технологии, мы создали для Вас столовые приборы, которые сделают Вашу ж Технология возведения подземных инженерных сооружений
Технология возведения подземных инженерных сооружений Жан Пиаже
Жан Пиаже Презентация на тему Разработка экспортных и импортных контрактов
Презентация на тему Разработка экспортных и импортных контрактов  ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ
ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ PowerPoint Show by Andrew
PowerPoint Show by Andrew СООО ПП Полесье - крупнейший производитель пластмассовых игрушек
СООО ПП Полесье - крупнейший производитель пластмассовых игрушек Портфолио успешной личности (9 КЛАСС)
Портфолио успешной личности (9 КЛАСС) Деятельность ОУ в реализации проекта «Профилактика правонарушений среди несовершеннолетних»
Деятельность ОУ в реализации проекта «Профилактика правонарушений среди несовершеннолетних» Библиотека университета Барселоны
Библиотека университета Барселоны Читаем классику без словаря
Читаем классику без словаря Аттракцион колотушка: маленькое яблоко
Аттракцион колотушка: маленькое яблоко Презентация на тему Эквадор
Презентация на тему Эквадор Рекламная кампания центра дополнительного образования
Рекламная кампания центра дополнительного образования Решение задач на построение сечений..pptx
Решение задач на построение сечений..pptx Образовательная система «ГРАНИ БОГАТСТВА» Чтобы заработать на жизнь, надо работать, но чтобы разбогатеть нужно представить что-то
Образовательная система «ГРАНИ БОГАТСТВА» Чтобы заработать на жизнь, надо работать, но чтобы разбогатеть нужно представить что-то Общественное здоровье
Общественное здоровье Мировой океан проблемы
Мировой океан проблемы Презентация на тему Типы собеседников
Презентация на тему Типы собеседников ПРИСТАВКИ
ПРИСТАВКИ Алканы
Алканы Коррупция как препятствие развития предпринимательской деятельности в регионе
Коррупция как препятствие развития предпринимательской деятельности в регионе Эвакуация населения
Эвакуация населения Внедрение нового формата ведения бизнеса
Внедрение нового формата ведения бизнеса Система работы по выполнению ФЗ № 120 «Об основах системы профилактики правонарушений и безнадзорности несовершеннолетних» в МОУ
Система работы по выполнению ФЗ № 120 «Об основах системы профилактики правонарушений и безнадзорности несовершеннолетних» в МОУ  Пушкин и Тамбовский край
Пушкин и Тамбовский край Подготовка к сочинению в форме эссе "Человек и война" 11 класс
Подготовка к сочинению в форме эссе "Человек и война" 11 класс Публикация материалов в сборнике проектных технологий
Публикация материалов в сборнике проектных технологий