Логарифмическая функция

Обобщение свойств логарифмической функции.
Выделение понятия области определения и выявление существенных признаков этого понятия для логарифмической функции.
Установление связей с наиболее трудными вопросами теории.
Расширение класса функций, графики которых можно построить с помощью преобразований.
Цели урока
y = log a x
y = log a (x + 4)
y = | log a x |

Этапы урока
Воспроизведение повторяемого материала.
Систематизация и обобщение ранее изученного.
Углубление и расширение знаний.
Проверка усвояемости изученного материала.

| Этап
Построение графиков функций:
Чем реже встречаются ошибки, тем они ценнее.
Ежи Лец

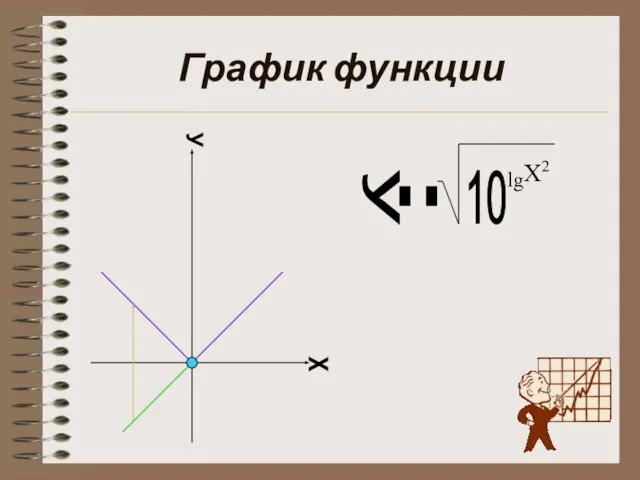
График функции
y
=
10
lg
X2
х
у

Функция У = Х logx2
Свойства функции Преобразование функции
D(y) = (0;1) u (1; )
a
=
M
logaM
У = Х logx2 = 2

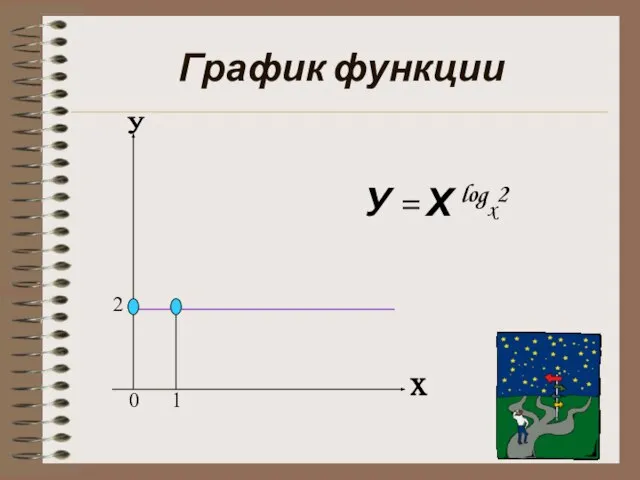
График функции
у
х
0 1
У = Х logx2
2

|| Этап
Делай, что можешь с тем, что у тебя есть, и там, где ты находишься.
Теодор Рузвельт.
Построение графика функции
У = log3 (X2 –9)/(|Х|-3)

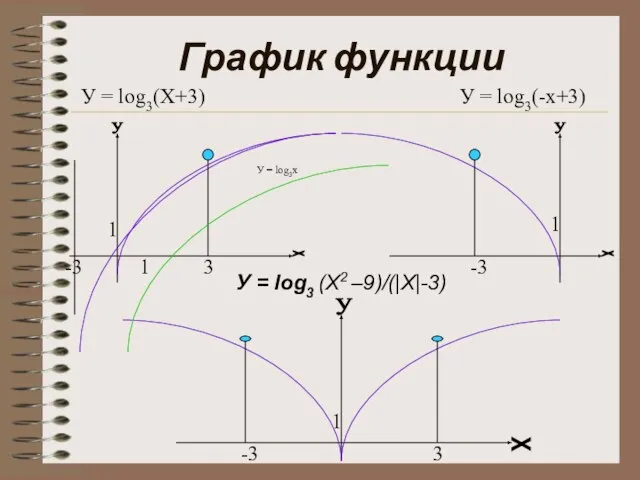
Функция У = log3 (X2 –9)/(|Х|-3)
Функция чётная –
график симметричен относительно оси ординат.
Расшифровка выражения.
Х, если Х > 0
-Х, если Х < 0
|X| =

Анализ выражения, стоящего под знаком логарифма
Х > 0.
(Х2 – 9) / (Х-3) > 0 при Х из [0; 3)U(3; ].
Вывод: функция принимает вид y = log3(x+3) в первом случае и y = log3(-x + 3) во втором случае.
Х < 0.
(Х2 – 9) / (-Х-3) > 0 при Х из [- ; -3)U(-3; 0].

График функции
У = log3(Х+3)
3
1
У = log3(-x+3)
1
-3
х
х
х
у
у
у
1
-3
3
У = log3 (X2 –9)/(|Х|-3)
1
У = log3x
-3

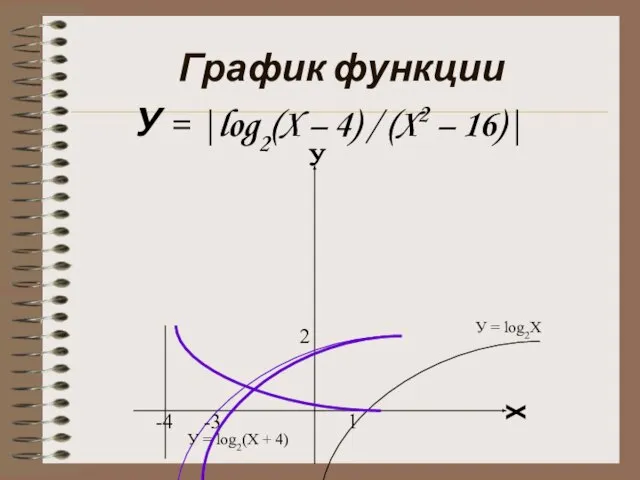
||| Этап
…Лучше знать лишнее, чем ничего не знать.
Сенека
Построение графика функции
У = |log2(X – 4) / (X2 – 16)|

График функции
У = |log2(X – 4) / (X2 – 16)|
-4
-3
1
2
У = log2Х
У = log2(Х + 4)
х
у