Логические основы алгоритмизации

История
Начало исследований в области формальной логики было положено Аристотелем в IV в. до н.э.
Однако математические подходы к этим вопросам были впервые указаны Джорджем Булем, который положил в основу математической логики алгебру логики.
Алгебра логики оперирует с высказываниями, т.е. повествовательными предложениями, о которых можно сказать (И) - Истинно оно или (Л) - Ложно.

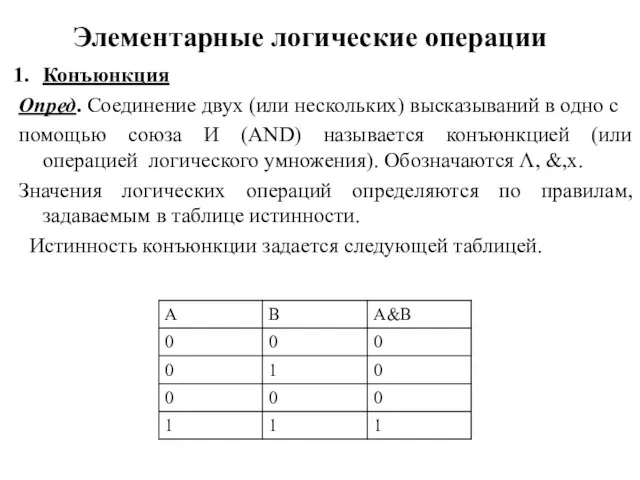
Элементарные логические операции
Конъюнкция
Опред. Соединение двух (или нескольких) высказываний в одно с
помощью союза И (AND) называется конъюнкцией (или операцией логического умножения). Обозначаются Λ, &,х.
Значения логических операций определяются по правилам, задаваемым в таблице истинности.
Истинность конъюнкции задается следующей таблицей.

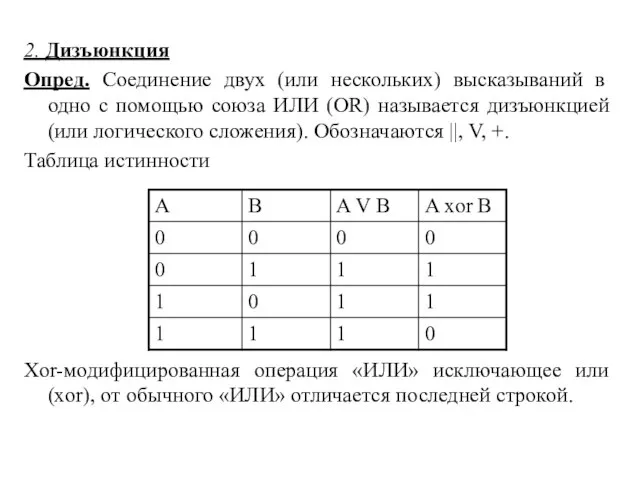
2. Дизъюнкция
Опред. Соединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ (OR) называется дизъюнкцией (или логического сложения). Обозначаются ||, V, +.
Таблица истинности
Xor-модифицированная операция «ИЛИ» исключающее или (хor), от обычного «ИЛИ» отличается последней строкой.

3. Отрицание (инверсия)
Опред. Присоединение частицы НЕ (NOT) к данному
высказыванию называется операцией отрицания (инверсии). Ā,
¬ А – «не А»
Таблица истинности

4. Эквивалентность
Служит для задания высказываний «тогда и только тогда, когда ... » или « если и только если» ...Обозначаются А ~ В (А ≡ В, А eqv В)
Таблица истинности

4. Импликация
Служит для задания так называемых условных высказываний «если…, то …» «когда ..., тогда ». Обозначаются А→ В, (А imp В).
Таблица истинности

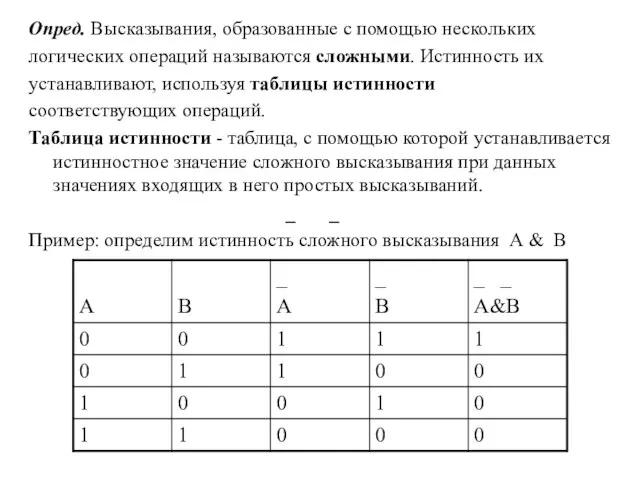
Опред. Высказывания, образованные с помощью нескольких
логических операций называются сложными. Истинность их
устанавливают, используя таблицы истинности
соответствующих операций.
Таблица истинности - таблица, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний.
_ _
Пример: определим истинность сложного высказывания А & В

Опред. Высказывания, у которых таблицы истинности
совпадают, называются равносильными. Для обозначения
используют знак = (А=В). _ _
Пример: рассмотрим сложное высказывание (А& В) V (А & В)
и составим таблицу истинности
если сравнить с таблицей истинности, для эквивалентности, то видно, что высказывания равносильны

Свойства логических операций
1. коммутативность
А& В = В & А
А V В = В V А
2. закон идемпотентности
А & А= А, А V А= А
3.ассоциативные законы
АV (В V С)= (АV В) V С= А V В V С
А & (В& С)= (А& В) & С= А&В&С
4.дистрибутивные законы
А & (В V С)= (А& В) V (А& С)
А V (В& С)= (А V В) & (А V С)
5. законы де Моргана
¬ (А&В)= ¬ А V ¬ В
¬ (А V В)= ¬ А & ¬ В
6. закон универсального множества
Х V 1= 1
Х & 1= Х
7.закон нулевого множества
Х V О = Х
Х & О = О

Схемная реализация базовых логических элементов
Логические элементы (ЛЭ) - это электронные схемы с одним или несколькими входами и одним выходом, через которые проходят электрические сигналы, представляющие 0,1.
Для реализации любой логической операции над двоичными сигналами достаточно элементов трех типов: И, ИЛИ, НЕ, функционально полная система, все остальные можно построить через них.
Существуют микросхемы, реализующие более сложные логические функции: И-НЕ, называемая операцией Шеффера (ĀВ), и ИЛИ- НЕ, называемая Стрелка Пирса (А+В).
Реальная аппаратура строится из логических элементов подобно тому, как сложная логическая функция получается путем комбинации более простых функций.

Схемная реализация базовых логических элементов.
Из логических элементов путем их комбинации строятся основные схемы компьютера.
Триггер - электронный прибор, имеющий два устойчивых состояния, является типичным запоминающим элементом, способным хранить 1 бит информации.
Регистр - совокупность триггеров, предназначенных для хранения числа в двоичном коде.
Сумматор - устройство, обеспечивающее суммирование двоичных чисел с учетом переноса из предыдущего разряда.

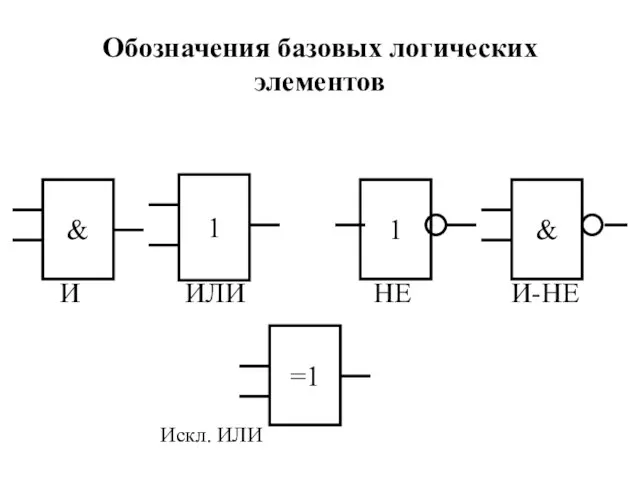
Обозначения базовых логических элементов
И ИЛИ НЕ И-НЕ
Искл. ИЛИ
&
1
=1
1
&

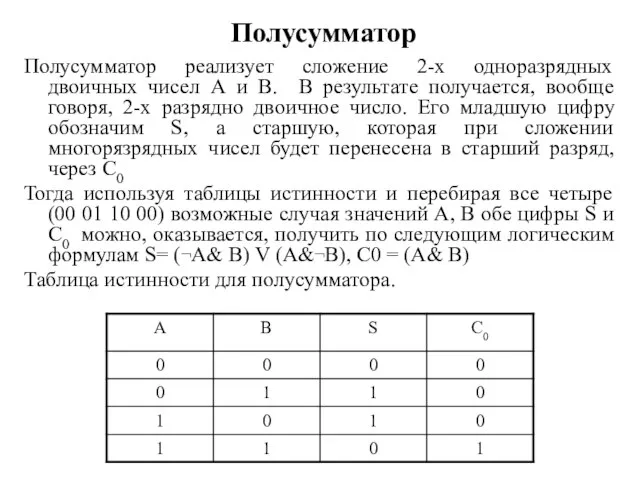
Полусумматор
Полусумматор реализует сложение 2-х одноразрядных двоичных чисел А и В. В результате получается, вообще говоря, 2-х разрядно двоичное число. Его младшую цифру обозначим S, а старшую, которая при сложении многорязрядных чисел будет перенесена в старший разряд, через С0
Тогда используя таблицы истинности и перебирая все четыре (00 01 10 00) возможные случая значений А, В обе цифры S и С0 можно, оказывается, получить по следующим логическим формулам S= (¬A& В) V (А&¬В), С0 = (А& В)
Таблица истинности для полусумматора.

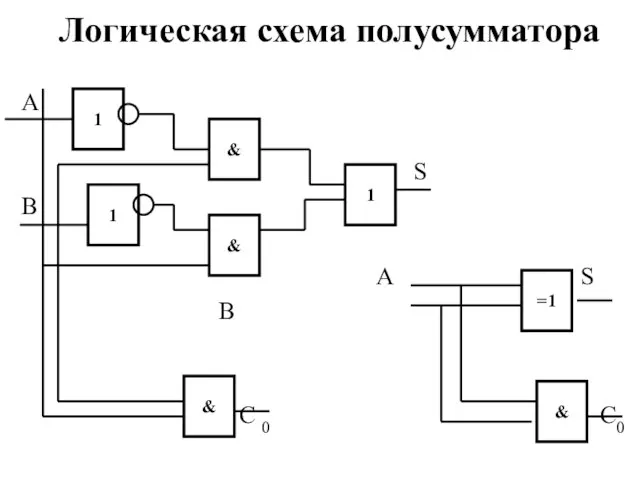
Логическая схема полусумматора
А
S
В
А S
В
C 0 C0
1
&
1
&
1
&
&
=1

Логические основы построения цифровых автоматов. Логический синтез переключательных и вычислительных схем. Синтез переключательных схем
Переключательная схема — схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также входов и выходов, на которые передается и с которых снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнутое разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то переменная х равна нолю. При этом два переключателя Х и
Х связаны таким образом, что когда Х замкнут, то Х разомкнут, и наоборот, Следовательно, если переключателю Х поставлена в соответствие логическая переменная х, то переключателю Х должна соответствовать переменная х.
Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нолю — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.

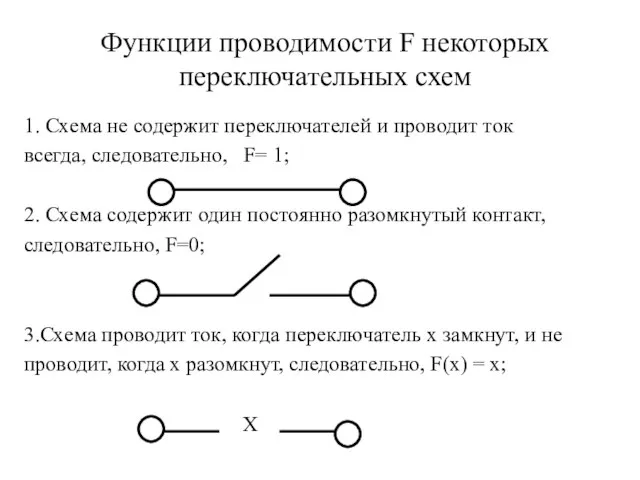
Функции проводимости F некоторых переключательных схем
1. Схема не содержит переключателей и проводит ток
всегда, следовательно, F= 1;
2. Схема содержит один постоянно разомкнутый контакт,
следовательно, F=0;
3.Схема проводит ток, когда переключатель х замкнут, и не
проводит, когда х разомкнут, следовательно, F(х) = х;
Х

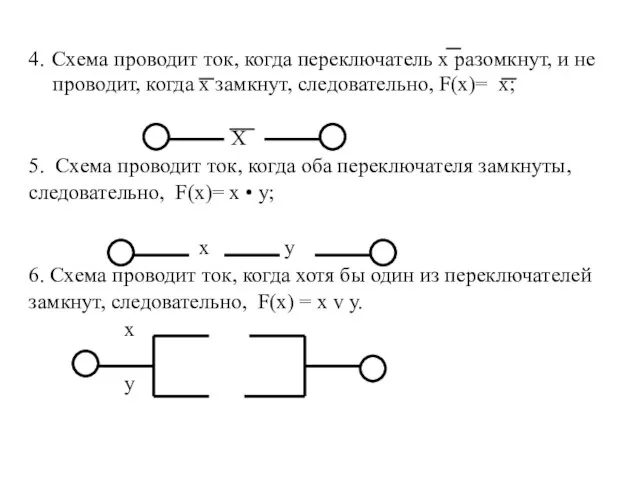
4. Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(х)= х;
Х
5. Схема проводит ток, когда оба переключателя замкнуты,
следовательно, F(х)= х • у;
х у
6. Схема проводит ток, когда хотя бы один из переключателей
замкнут, следовательно, F(х) = х v у.
х
у

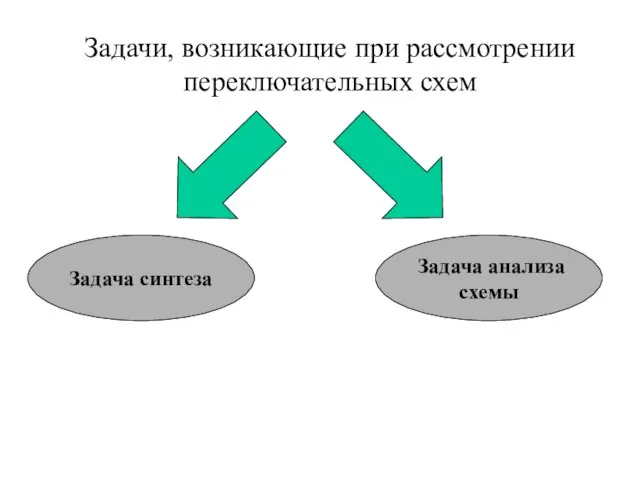
Задачи, возникающие при рассмотрении переключательных схем
Задача синтеза
Задача анализа схемы

Этапы синтеза переключательной схемы
1. Составление функции проводимости по заданным условиям
2. Упрощение этой функции.
3. Построение соответствующей схемы.

Этапы анализа схемы
1. Определение значений функции проводимости при всех возможных наборах, входящих в эту функцию переменных.
2. Получение упрощенной формулы.

СКНФ и СДНФ
Совершенной дизъюнктивной нормальной формой (СДНФ) называют наиболее полную форму записи логического выражения. Эта форма записи представляет собой сумму, каждое слагаемое которой является произведением всех входных аргументов или их инверсий, например:
F = ¬A¬В¬С + ¬А В¬С + А В¬С + А В С.
СДНФ является избыточной, но логические функции, записанные в СДНФ, легко сравнивать между собой и их удобно преобразовывать в таблицы истинности. Булево выражение, полученное из таблицы истинности логической функции, имеет совершенную дизъюнктивную нормальную форму.
Еще одной формой записи логического выражения является совершенная конъюнктивная нормальная форма (СКНФ). Это произведение сомножителей, каждый из которых является суммой всех входных аргументов или их отрицаний, например:
F = (¬А + В +¬С ) (¬А + В + С ) ( А +¬В + С ) ( А + В + С ).

Этапы синтеза переключательных схем
1. Образование СДНФ* (СКНФ**) функции по заданной таблице истинности.
* совершенной дизъюнктивной нормальной формой
** совершенной конъюнктивной нормальной формой
2. Упрощение этой функции (преобразованию СДНФ (СКНФ) в формулу с наименьшим числом вхождений переменных);
3. Построение соответствующей схемы.

Образование СДНФ функции по заданной таблице истинности
Этот этап включает в себя:
в заданной таблице истинности выделяют наборы значений аргументов, при которых функция принимает единичное значение;
для каждого выделенного набора образуется конституэнта единицы, принимающая единичное значение при данном наборе значений аргументов;
составляется логическая сумма образованных конституэнт единицы.
Для образования конституэнты единицы С1i, принимающей единичное значение в i-ом наборе значений аргументов необходимо составить логическое произведение аргументов, в которое аргументы, принимающие в i- м наборе единичное значение, входят без знака отрицания, а аргументы, принимающие в i –м наборе новое значение, входят со знаком отрицания.

Образование СКНФ функции
1. В таблице выделяются наборы значений аргументов, при которых функции принимает нулевое значение;
2. Для каждого выделенного набора образуется конституэнта поля, принимавшая нулевое значение при данном наборе значений аргументов;
3. Составляется логическое произведение образованных конституэнт ноля.

Упрощение функции
При преобразовании СДНФ (СКНФ) в формулу с наименьшим числом вхождений переменных (миними­зация формулы) используют аксиомы и законы булевой алгебры:
вынос за скобки XY v XZ= X(Y v Z);
полное склеивание ХY v Х¬Y = X;
поглощение Х v XY= X;
минимизация по методу Квайна;
минимизация с использованием карт Карно или диаграмм Вейча.
При минимизации по методу Квайна предполагается, что исходная функция задана в СДНФ.
Введем несколько определений. Конъюнкция, получаемая в результате склеивания двух конституэнт единицы, называется импликантой. Импликанта поглощает конституэнты единицы, при склеивании которых она образовалась.

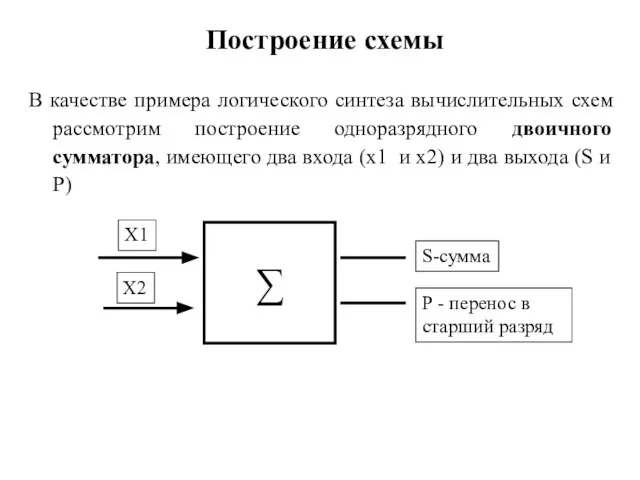
Построение схемы
В качестве примера логического синтеза вычислительных схем рассмотрим построение одноразрядного двоичного сумматора, имеющего два входа (х1 и х2) и два выхода (S и P)
∑
S-сумма
Р - перенос в старший разряд
Х1
Х2

Зададим таблицу истинности сумматора.
Представим выходные функции S и P в виде СДНФ: S=f1(x1,x2) = ¬ x1 х x2 + x1 х ¬x2 = х1 хоr x2
P=f2(x1, x2) = x1 х x2

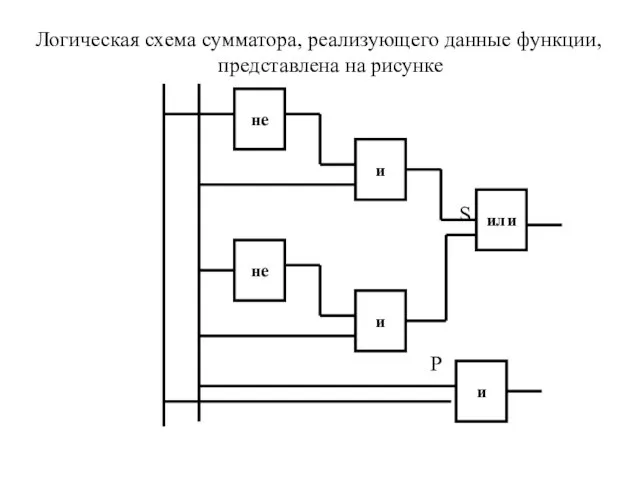
Логическая схема сумматора, реализующего данные функции, представлена на рисунке
S
P
не
и
и
или
и
не

Для логических схем (И, ИЛИ, НЕ) существуют типовые технические
схемы (логические элементы), реализующие их на полупроводниковых структурах, т.е. аппаратно.
Использование знаков 0 и 1 подчеркивает некоторое соответствие между значениями логических переменных и функций в математической логике и цифрами в двоичной системе счисления.
Это позволяет описывать работу логических схем ПК и проводить их анализ и синтез с помощью математического аппарата алгебры логики. Любое устройство ПК - некоторый функциональный преобразователь. Причем входы- значения логических переменных, выход - значения логических функций, т.е. устройство ПК ~ функция.
Логический элемент- часть электронной логической схемы, которая реализует элементарную логическую функцию.

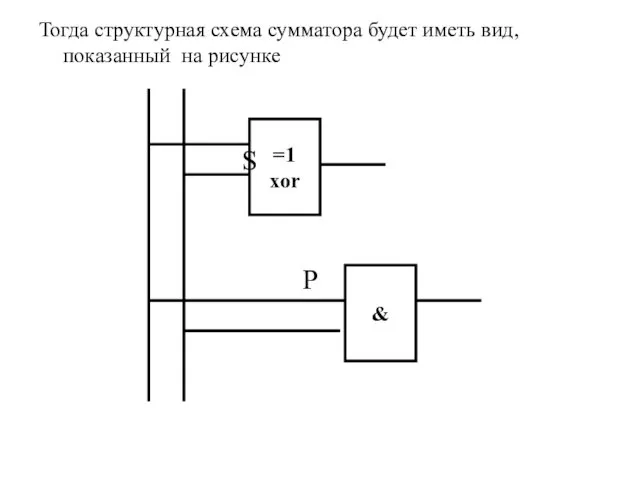
Тогда структурная схема сумматора будет иметь вид, показанный на рисунке
S
P
=1
xor
&