Содержание
- 2. Цель урока рассмотреть понятия «конъюнкция, дизъюнкция, инверсия, таблица истинности, логическая схема»; научить технологии составления таблиц истинности
- 3. конъюнкция; дизъюнкция; инверсия; таблица истинности; логическая схема; логическая функция. Новые понятия
- 4. Логические принципы работы компьютера 3 основные логические операции, лежащие в основе всех выводов компьютера: и, или,
- 5. Элементарные логические операции. Таблицы истинности. Логические схемы. 1. Конъюнкция -логическое умножение. Обозначение: И; AND; &; ^;
- 6. Элементарные логические операции. Таблицы истинности. Логические схемы. 2. Дизъюнкция – логическое сложение. Обозначение – или; OR;
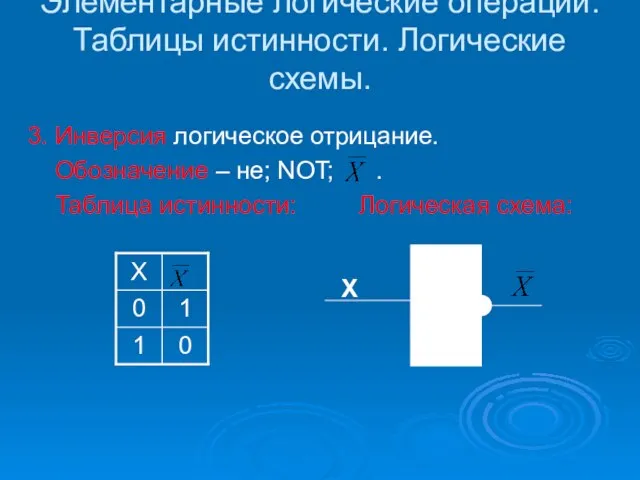
- 7. Элементарные логические операции. Таблицы истинности. Логические схемы. 3. Инверсия логическое отрицание. Обозначение – не; NOT; .
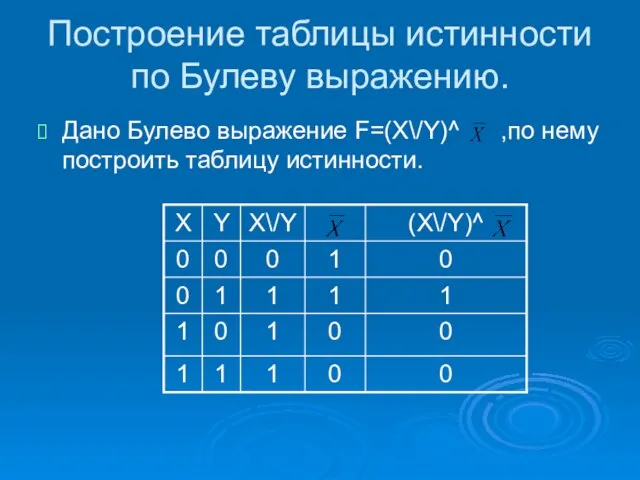
- 8. Построение таблицы истинности по Булеву выражению. Дано Булево выражение F=(X\/Y)^ ,по нему построить таблицу истинности.
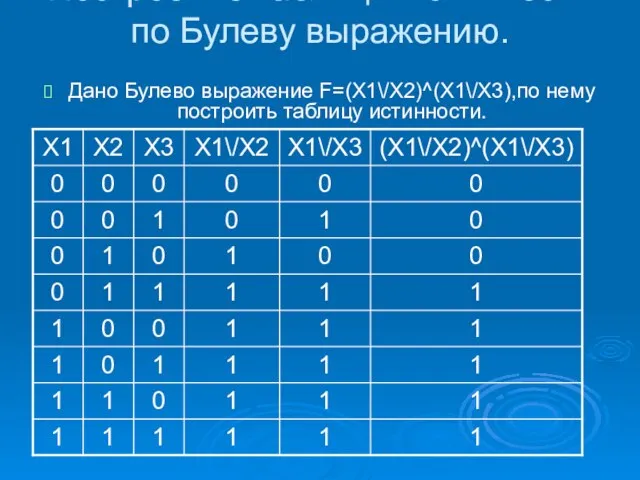
- 9. Построение таблицы истинности по Булеву выражению. Дано Булево выражение F=(X1\/X2)^(X1\/X3),по нему построить таблицу истинности.
- 10. Дано Булево выражение , по нему построить таблицу истинности.
- 12. Дано Булево выражение , по нему построить таблицу истинности.
- 14. Комплекс упражнений для снятия СКС Пальминг Цель: релаксация глазных мышц, улучшение кровообращения Положение: сидя Инструкции: Натирайте
- 15. Комплекс упражнений для снятия СКС Самомассаж лица
- 16. Выполните тест по теме: «Логические принципы работы компьютера» Тестировщик.exe
- 17. Домашнее задание: Конспект. Дано Булево выражение , по нему построить таблицу истинности.
- 18. В начале XVIII века по просьбе великого немецкого ученого Готфрида Вильгельма Лейбница, внесшего большой вклад в
- 19. Урок понравился
- 20. Урок оставил равнодушным
- 22. Скачать презентацию















 Электроснабжение части потребителей промышленного района г. Оренбурга
Электроснабжение части потребителей промышленного района г. Оренбурга Классификация мотивов учения
Классификация мотивов учения 20180104_rossiya_ustremlennaya_v_budushchee
20180104_rossiya_ustremlennaya_v_budushchee Буклет Тыква
Буклет Тыква Университетский лицей представляет
Университетский лицей представляет Личный фотоальбом
Личный фотоальбом Моя спортивная семья
Моя спортивная семья Эволюция техники и значение образования в этом процессе
Эволюция техники и значение образования в этом процессе Презентация на тему Куда текут реки (1 класс)
Презентация на тему Куда текут реки (1 класс) Презентация СИМАРГЛ
Презентация СИМАРГЛ Всемирный день памяти жертв дорожно-транспортных происшествий
Всемирный день памяти жертв дорожно-транспортных происшествий Развитие познавательных творческих способностей учащихся во внеклассной работе
Развитие познавательных творческих способностей учащихся во внеклассной работе Презентация на тему животные из пластилина
Презентация на тему животные из пластилина План работы Нижнетагильского местного отделения КПРФ на 2018-2021 г
План работы Нижнетагильского местного отделения КПРФ на 2018-2021 г Англичане
Англичане Oracle
Oracle Проект Cossa
Проект Cossa Презентация на тему Умножение и деление десятичных дробей на натуральное число
Презентация на тему Умножение и деление десятичных дробей на натуральное число 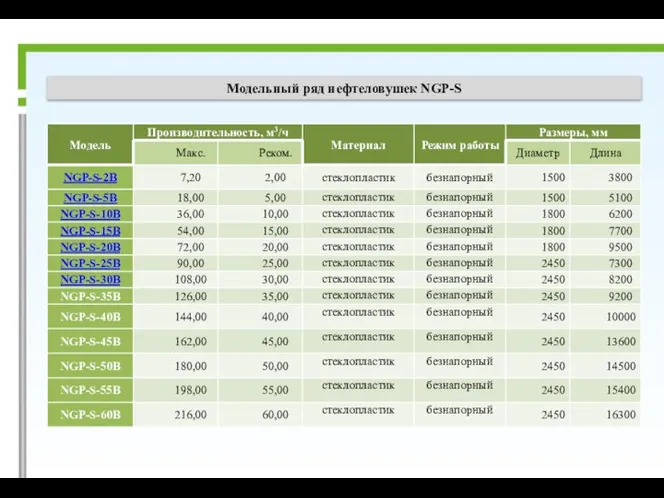 Модельный ряд нефтеловушек NGP-S
Модельный ряд нефтеловушек NGP-S Понятие вектора
Понятие вектора «Свободная цена»: решение для независимых музыкантов и НКО
«Свободная цена»: решение для независимых музыкантов и НКО 873464
873464 Цикл о Кухулине. Ирландский эпос
Цикл о Кухулине. Ирландский эпос Арт лагерь Нескучное лето!
Арт лагерь Нескучное лето! Экологическое право
Экологическое право Живопись XIX века
Живопись XIX века Стили речи
Стили речи Большой брат следит за вами
Большой брат следит за вами