Математическая статистика

В математической статистике разрабатываются теории и методы обработки информации о массовых явлениях и их назначении
Для этого проводится статистическое исследование, материалом для которого являются статистические данные

Статистические данные – это сведения о числе объектов какого - либо множества, обладающих некоторым признаком
Пример.
Сведения о числе отличников в каждом ССУЗе, сведения о числе разводов на число вступивших в брак

На основании статистических данных можно делать научно – обоснованные выводы
Для этого статистические данные определенным образом должны быть систематизированы и обработаны
Математическая статистика изучает математические методы систематизации, обработки и использования статистических данных для научных и производственных целей

Основной метод обработки данных – выборочный
Основа - теория вероятности, в которой изучаются математические модели реальных случайных явлений
Математическая статистика связывает реальные случайные явления и их математические вероятностные модели
Математическая статистика возникла в 17 веке одновременно с теорией вероятности

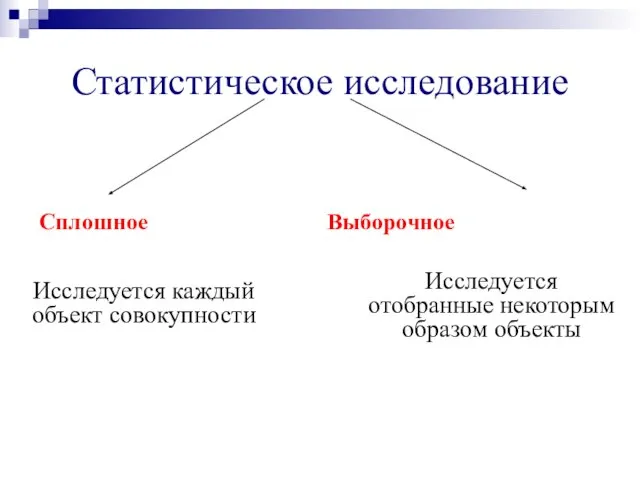
Статистическое исследование
Сплошное Выборочное
Исследуется каждый объект совокупности
Исследуется отобранные некоторым образом объекты

Генеральная совокупность – совокупность всех исследуемых объектов
Выборочная совокупность (выборка) – совокупность случайно отобранных объектов
Случайный отбор – это такой отбор, при котором все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку

Выборка
повторная бесповторная
Объект извлекается из генеральной совокупности, исследуется и возвращается в генеральную совокупность, берется следующий, исследуется и возвращается и т.д.
Объект извлекается из и не возвращается, берется генеральной совокупности, исследуется следующий

Объём выборки – это число равное количеству объектов генеральной или выборочной совокупности
Пример.
Из 10000 изделий для контроля отобрали 100 изделий
Объем генеральной совокупности равен 10000, объем выборки – 100

Математическая статистика занимается вопросом: можно ли установив свойство выборки, считать, что оно присуще всей генеральной совокупности
Для этого выборка должна быть достаточно представительной, т.е. достаточно полно отражать изучаемое свойство объектов
Поэтому отбор объектов в выборку осуществляется случайно, а изучаемому свойству должна быть присуща статистическая устойчивость: при многократном повторении исследования наблюдаемые события повторяются достаточно часто (статистическая устойчивость частот)

Для статистической обработки результаты исследования объектов, составляющих выборку, представляют в виде числовой выборки (последовательность чисел)
Разность между наибольшим значением числовой выборки и наименьшим называется размахом выборки

Рассмотрим числовую выборку объема n, полученную при исследовании некоторой генеральной совокупности
Значение x1 встречается в выборке n1 раз
x2 встречается n2 раза
…….
xn встречается nn раз
Числа называются частотами значений
Отношения частот к объему выборки
называются относительными частотами значений

Если составлена таблица в первой строке значения выборки, а во второй частоты значений, то она задает статистический ряд, если второй строке относительные частоты значений, то такая таблица задает выборочное распределение

Пример.
Для выборки определить объем, размах, найти статистический ряд и выборочное распределение:
3, 8, -1, 3, 0, 5, 3, -1, 3, 5
Объем: n = 10, размах = 8 – (-1) =9
Статистический ряд:
Выборочное распределение:
(убеждаемся 0,2 + 0,1 + 0,4 + 0,2 + 0,1 = 1)

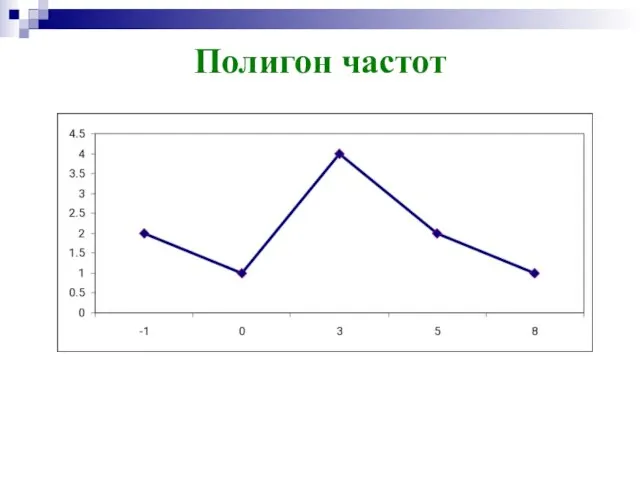
Графические изображения выборки
Если выборка задана значениями и их частотами или статистическим рядом, то строится полигон
Полигон частот Полигон относительных частот
Это ломаная с вершинами в точках
Это ломаная с вершинами в точках

Полигон частот

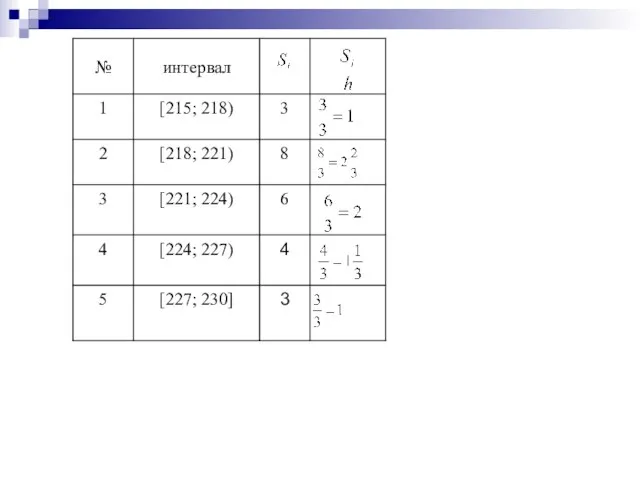
При большом объеме выборки строится гистограмма
Гистограмма частот гистограмма относительных частот
Для построения гистограммы промежуток от наименьшего значения выборки до наибольшего разбивают на несколько частичных промежутков длины h
Для каждого частичного промежутка подсчитывают сумму частот значений выборки, попавших в этот промежуток (Si)
Значение выборки, совпавшее с правым концом частичного промежутка (кроме последнего промежутка), относится к следующему промежутку
Затем на каждом промежутке, как на основании, строим прямоугольник с высотой
Ступенчатая фигура, состоящая из таких прямоугольников, называется гистограммой частот
Площадь такой фигуры равна объёму выборки

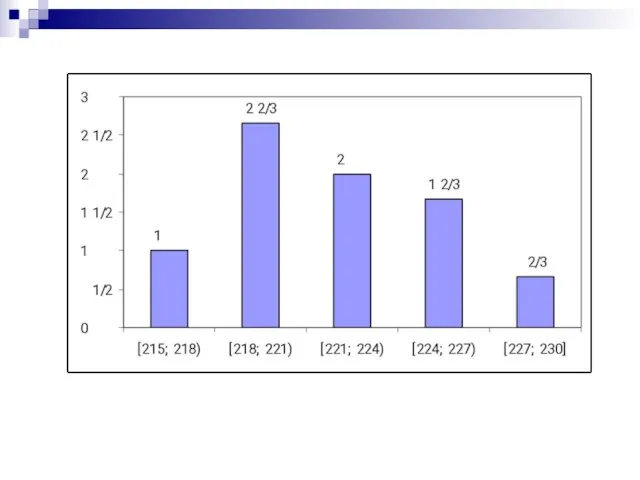
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых являются частичные промежутки длины h, а высотой отрезки длиной
где ωi – сумма относительных частот значений выборки, попавших в i промежуток
Площадь такой фигуры равна 1
Пример.
В результате измерения напряжения в электросети получена выборка. Построить гистограмму частот, если число частичных промежутков равно 5

218, 224, 222, 223, 221, 220, 227, 216, 215, 220, 218, 224, 225, 219, 220, 227, 225, 221, 223, 220, 217, 219, 230, 222
n = 24
Наибольшее значение – 230
Наименьшее значение – 215
Интервал: 230 – 215 = 15
Длина частичных промежутков:
Составим таблицу:

Выборочные характеристики
Для выборки объема n
Выборочное статистическое ожидание (выборочное среднее) – это среднее арифметическое значений выборки
Если выборка задана статистическим рядом, то

Выборочная дисперсия – это среднее арифметическое квадратов отклонений значений выборки от выборочного среднего
Если выборка задана статистическим рядом, то

Несмещенная выборочная дисперсия
Пример.
Для выборки найти
Выборка: 4, 5, 3, 2, 1, 2, 0, 7, 7, 3
n = 10