Математические и логические основы информатики

Система счисления -
совокупность приемов и правил записи чисел с помощью определенного набора символов (с.с.)

Системы счисления
Позиционные системы счисления
Непозиционные системы счисления
Значение цифры зависит от ее положения в числе
Значение цифры не зависит от ее положения в числе

Римская непозиционная система счисления
I (1)
V (5)
X (10)
L (50)
C (100)
D (500)
M (1000)

Значение цифры не зависит от ее местоположения в числе
XXX = 30
MCMXCVIII = 1000+(1000-100)+(100-10)+5+1+1+1=1998

Какая система счисления используется повсеместно в наше время?
Десятичная
Сколько цифр в десятичной системе?
Десять
Какие это цифры?
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Что является основанием десятичной системы?
Число 10
Как вы думаете, почему люди используют десятичную систему, а не семеричную?
Десять пальцев на руках

Вспомните, какие системы счисления встречаются в нашей жизни по сей день?
Двенацетиричная (количество месяцев в году, количество часов, количество знаков зодиака); семеричная (семь дней в неделе, обилие пословиц и поговорок с числом семь)
Шестидесятеричная система счисления (временная мера)

Меняется ли десятичное число, если переставить в нем цифры?
2381
8312
8 в разряде десятков
8 в разряде тысяч

Подобные системы называют позиционными.
Это системы в которых цифры в числе имеют разный «вес» (разряд).
«Вес» цифры зависит от ее места (позиции) в числе.

2381 = 2000 + 300 + 80 + 1 = 2·103 + 3·102 + 8·101 + 1·100
Развернутая форма представления десятичного дробного числа
1 0 -1 -2
Развернутая форма представления целого десятичного числа
23,81 = 20 + 3 + 0,8 + 0,01 = 2·101 + 3·100 + 8·10-1 + 1·10-2
3 2 1 0

Перевод чисел из любой позиционной системы в десятичную
3125 = 3·52 + 3·51 + 3·50 =
3·25 + 3·5 +3·1= 75 + 15 + 3 =9310
2 1 0

В позиционных системах основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в одинаковых позициях.

В вычислительной технике применяют 4 системы счисления:
Двоичная – 0, 1 (основание с.с. – 2)
Десятичная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (основание с.с. – 10)
Восьмеричная – 0, 1, 2, 3, 4, 5, 6, 7 (основание с.с. – 8)
Шестнадцатеричная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F (основание с.с. – 16)

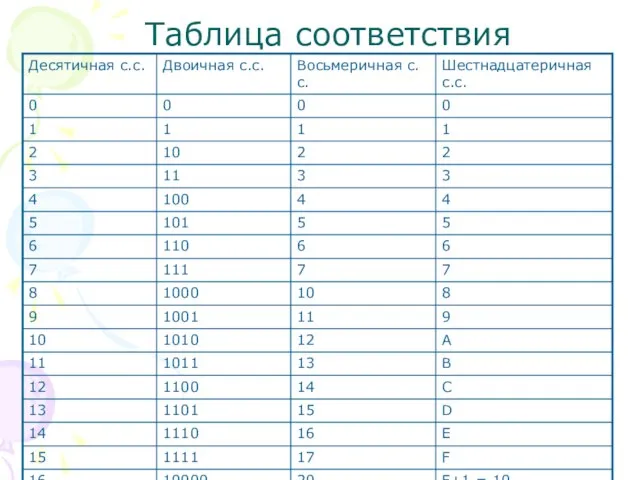
Таблица соответствия

Перевод десятичного числа в другую позиционную систему счисления