Слайд 2Задача 1
В коридоре детского сада стояли двухколесные и трехколесные велосипеды. Катя подсчитала,

что колес 18, а рулей всего 7.
Сколько было двухколесных велосипедов?
Слайд 3Задача 2
Весь класс, в котором учатся Маша и Даша, выстроился в колонну

по одному. Позади Маши стоит 16 человек, включая Дашу, а впереди Даши стоит 14 человек. Сколько ребят в классе, если между Машей и Дашей стоит 7 человек?
Слайд 4Задача 3
Часовщик смотрит на 4 будильника. Только один из этих будильников показывает

верное время. Из оставшихся один спешит на 20 минут, другой отстает на 20 минут, а третий вовсе стоит.
Какое время показывает правильно идущий будильник?
Слайд 5Задача 4
Во сколько раз миллион миллиардов отличается от миллиарда миллионов?

Слайд 6Задача 5
Длинную нитку сложили вдвое, еще раз вдвое и еще раз вдвое.

Получившуюся толстую «нитку» разрезали на 2 части и разобрали обратно на тонкие ниточки. Оказалось, что две из этих ниточек, имеют длины 4 см и 9 см. Какова наименьшая возможная длина исходной нитки?
Слайд 7Задача 6
Четверо ребят обсуждали ответ к задаче. Коля сказал: «Это число 9».

Роман: «Это простое число».
Катя: «Это чётное число».
А Наташа сказала, что это число 15. Назовите правильный ответ, если мальчики и девочки ошиблись по одному разу.
Слайд 8Задача 7
В ряд выписали 11 натуральных чисел так, что сумма любых трех

соседних равна 21. На первом месте стоит число 7, а на девятом 6. Какое число стоит на втором месте?
Слайд 9Задача 8
Сколько треугольников изображено на рисунке?

Слайд 10Задача 9
Из чисел, квадраты которых делятся на 24, выбрали самое маленькое. Чему

равна сумма цифр этого числа?
Слайд 11Задача 10
Влажность скошенной травы равна 60%, а влажность сена – 15%. Сколько

килограммов сена получится из тонны травы?
Слайд 12Задача 11
Крыша покрыта одинаковыми прямоугольными листами кровли, которые уложены в 8 рядов

(снизу вверх). Каждый следующий ряд перекрывает предыдущий на 0,1 своей ширины. Какая часть крыши покрыта в 2 слоя?
Слайд 13Задача 12
Сколько десятизначных чисел, кратных 9, имеют в своей записи только 0

и 1?
Слайд 14Задача 13
Семья Васи приехала на дачу на машине в 16.00. Если бы

скорость, с которой они ехали, была на 25% больше, то они приехали бы в 14.30.
В какое время они выехали из дома?
Слайд 16Задача 15
Найдите сумму коэффициентов и свободного члена многочлена, полученного после раскрытия скобок

и приведения подобных членов в выражении
2009 – (2008-2009x)2008.
Слайд 17Задача 16
На столе лежат пятиугольники и шестиугольники. Всего у них ровно 37

вершин.
Сколько всего пятиугольников на столе?
Слайд 18Задача 17
Четырехзначное число начинается с цифры 5.
Эту цифру переставили в

конец числа. Полученное число оказалось на 747 меньше исходного.
Какова сумма цифр этого числа?
Слайд 19Задача 18
Диагональ делит четырехугольник с периметром 31 см на два треугольника с

периметрами 21 см и 30 см. Чему равна длина этой диагонали?
Слайд 20Задача 19
Четное натуральное число n имеет ровно 5 натуральных делителей, включая 1

и n. Сколько делителей имеет число 10n?
Слайд 21Задача 20
Сколько существует различных целых чисел, у которых самый большой делитель (не

считая самого числа) равен 91?




















 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр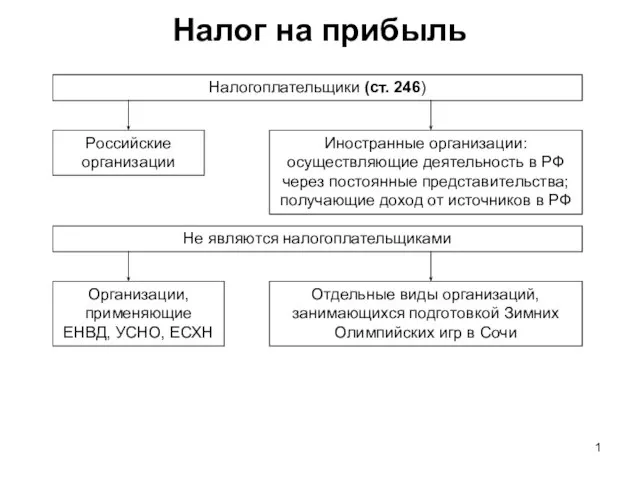 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология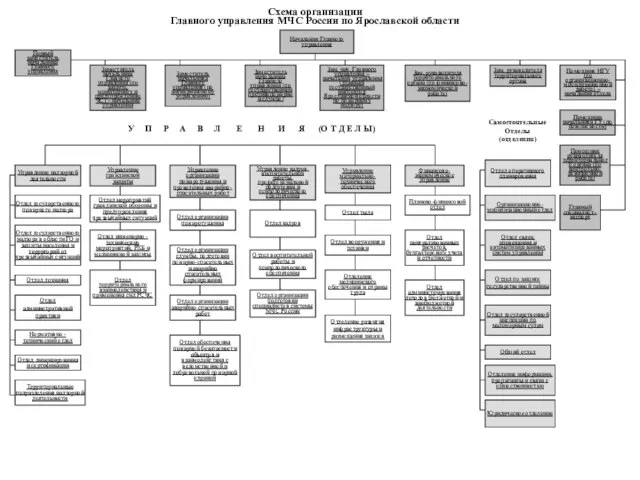 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва