Математическое описание экосистемы пелагиали озера БайкалЗоркальцев В.И.(д.т.н., Иркутск) Казазаева А.В.(ИГУ, асп., Иркутск) Мокры

Цели
1. Выработка системы (количественно и понятийно взаимосвязанных) представлений о динамике жизнедеятельности отдельных видов организмов пелагиали оз.Байкал и их взаимодействий.
2. Систематизация накопленных данных и освоение знаний. Оценка параметров динамики жизнедеятельности и взаимодействия организмов по имеющимся экспериментальным данным.
3. Анализ полноты и надежности (в т.ч. противоречивости) накопленных данных отдельных экспериментальных исследований.

Цели
4. Построение имитационной модели функционирования экосистемы пелагиали оз.Байкал (динамики жизнедеятельности и взаимодействия основных видов).
5. Изучение механизмов функционирования экосистемы оз.Байкал на имитационной модели:
- для выработки гипотез относительно механизмов взаимодействия основных видов организмов;
- верификация имеющихся данных и оценка адекватности вариантов модели;
- для уточнения направлений проведения натурных экспериментов.

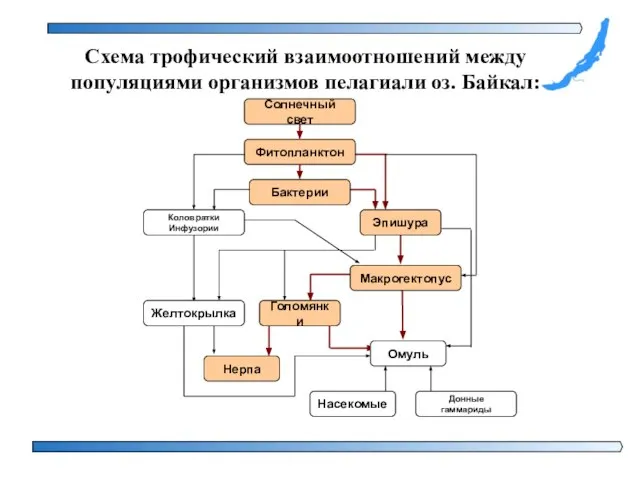
Схема трофический взаимоотношений между
популяциями организмов пелагиали оз. Байкал:

Характеристика модели
(планируемой к разработке в ближайшее время)
Состав: - Эпишура;
- Макрогектопус;
- Большая голомянка;
- Малая голомянка.
В основу построения модели положены уравнения Лотке – Вольтерра.
Модель учитывает динамику развития особи и описывает каждую популяцию в виде взаимодействующих возрастных групп.
Степень подробности: годовая и сезонная модели.

Инструменты
Для расчета параметров стационарного состояния и начальных условий используется Microsoft Excel.
Для конструирования моделей динамики популяций используется система моделирования Dynamo (реализованная И.В.Мокрым в ИСЭМ СО РАН).

План исследования
1. Разработка методов оценки параметров динамики популяций в стационарном состоянии.
2. Построение модели межгодовой динамики численности популяций макрогектопус, большая и малая голомянки.
3. Построение межгодовой модели взаимодействия потоков биомасс в трофическом звене популяций макрогектопуса, большой и малой голомянок.
____________________________________________________
4. Оценка параметров и построение стационарной модели сезонной динамики популяций эпишуры и макрогектопуса.
5. Построение обобщенной модели динамики популяций эпишуры, макрогектопуса, большой и малой голомянок.

Часть I
Разработка методов оценки параметров динамики популяций в стационарном состоянии

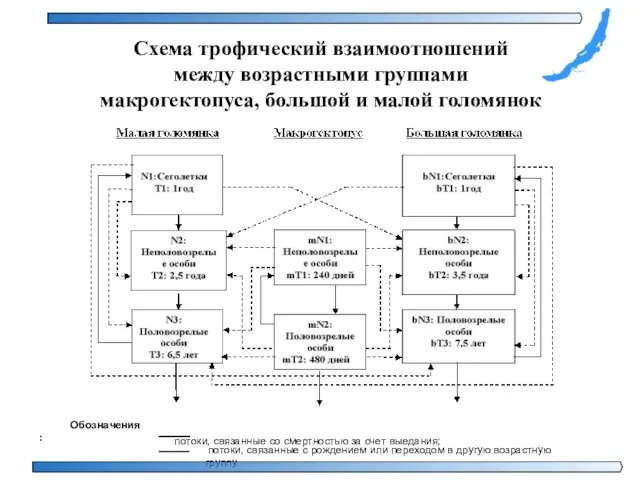
Схема трофический взаимоотношений
между возрастными группами
макрогектопуса, большой и малой голомянок
Обозначения :
потоки, связанные со смертностью за счет выедания;
потоки, связанные с рождением или переходом в другую возрастную группу.

Основные гипотезы для оценки параметров в стационарном состоянии
1. Особи популяции характеризуются только возрастом и усреднены по всем остальным параметрам, в том числе по половому признаку.
2. Смертность особей одной возрастной группы определяется единым коэффициентом смертности для данной возрастной группы.
3. Для каждой популяции функция репродуктивности определяется тремя параметрами: временем полового созревания, периодом репродуктивности и постоянным коэффициентом репродуктивности.
4. Коэффициент смертности для каждой возрастной группы не меняется во времени.
5. Численность особей в каждой из возрастных групп не меняется во времени.

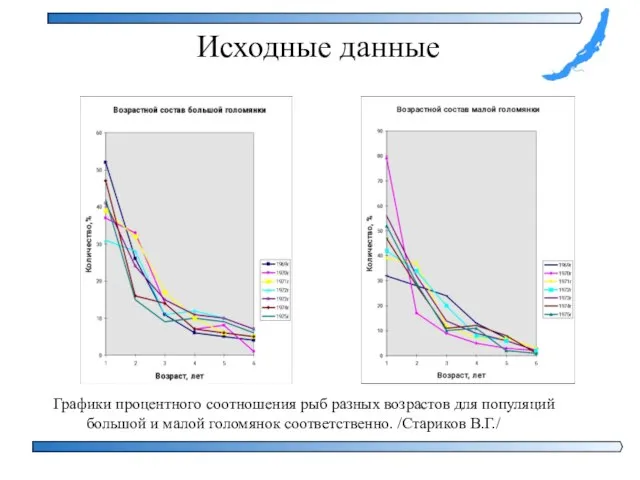
Исходные данные
Графики процентного соотношения рыб разных возрастов для популяций большой и малой голомянок соответственно. /Стариков В.Г./

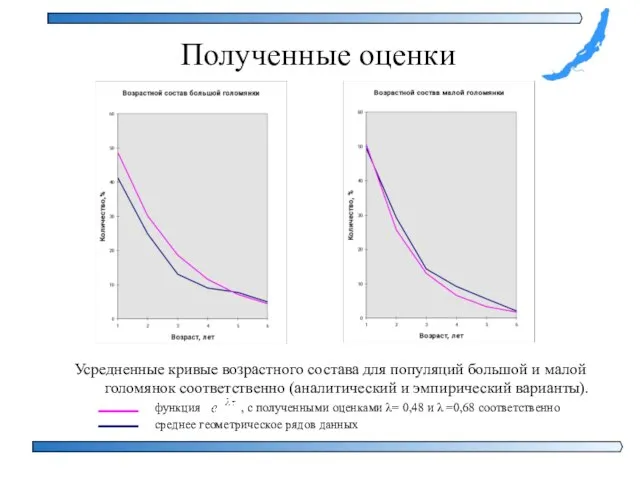
Полученные оценки
На основании гипотезы - кривая возрастного состава
описывается функцией , где λ – коэффициент смертности, а τ – возраст, кривые возрастного состава были прологарифмированы и методом наименьших квадратов были получены следующие оценки коэффициентов смертности для взрослых особей:
- для малой голомянки ;
- для большой голомянки .

Полученные оценки
Усредненные кривые возрастного состава для популяций большой и малой голомянок соответственно (аналитический и эмпирический варианты).
функция , с полученными оценками λ= 0,48 и λ =0,68 соответственно
среднее геометрическое рядов данных

Методики оценки коэффициентов смертности
- через Р/В–коэффициент (показывает отношение продукции популяции к ее биомаcсе), основан на фактических данных о продукции и биомассе популяции;
- через функцию репродуктивности, в основу метода положены перечисленные гипотезы и коэффициенты рождаемости*.
* Коэффициенты рождаемости имеют интервальный характер. Они получены на основе анализа разных публикаций. Единой методики нет.

Полученные оценки
Коэффициентов рождаемости:
- особи большой голомянки – 500 личинок/год
- особи малой голомянки – 597,6 личинок/год
- особи макрогектопуса – [87-206] яиц/год
Коэффициентов смертности:
- взрослых особей большой голомянки – 0,48;
- взрослых особей малой голомянки – 0,68;
- сеголеток большой и малой голомянок ≈ 5,69.
особей обеих возрастных групп популяции
макрогектопуса ≈ 5,69.

Часть II
Построение модели межгодовой динамики численности популяций макрогектопус, большая и малая голомянки

Общий вид балансового уравнения для численности одной из возрастных групп макрогектопуса, большой или малой голомянки
(1)
где i – индекс возрастной группы;
– поток численности особей перешедших из предыдущей
группы или поток вновь родившихся, в случае 1-ой
возрастной группы ;
– коэффициент смертности данной возрастной группы;
– численность данной возрастной группы;
– количество особей перешедших в следующую возрастную
группу (в случае последней возрастной группы – количество
умерших по достижении предельного возраста), где
параметр, определяющий максимальное
время пребывания особи в данной группе.

Структура вспомогательных моделей динамики численности популяций макрогектопуса, большой и малой голомянок
Для малой голомянки: Для большой голомянки:
Для макрогектопуса:

Значения параметров моделей в состоянии равновесия популяций
В случае система уравнений описывает равновесное состояние популяций.
Значения численностей возрастных групп популяций в состоянии равновесия рассчитываются по формулам:
.
Численные значения параметров:
Малая голомянка –
Большая голомянка –
Макрогектопус –

Начальные условия для моделей динамики численности популяций макрогектопуса, большой и малой голомянок в точке равновесия
Для малой голомянки: Для большой голомянки:
Для макрогектопуса:
Модели находятся в устойчивом равновесии.

Обратные связи в модели динамики численности популяций макрогектопуса, большой и малой голомянок
Коэффициент смертности динамически зависит от численности старших возрастных групп голомянок:
Коэффициент репродуктивности для макрогектопуса – величина постоянная; для голомянок он пересчитывается динамически, согласно гипотезе - репродуктивность особи пропорциональна рациону :
Для малой голомянки –
Для большой голомянки –
В данной модификации модель ведет себя устойчиво.

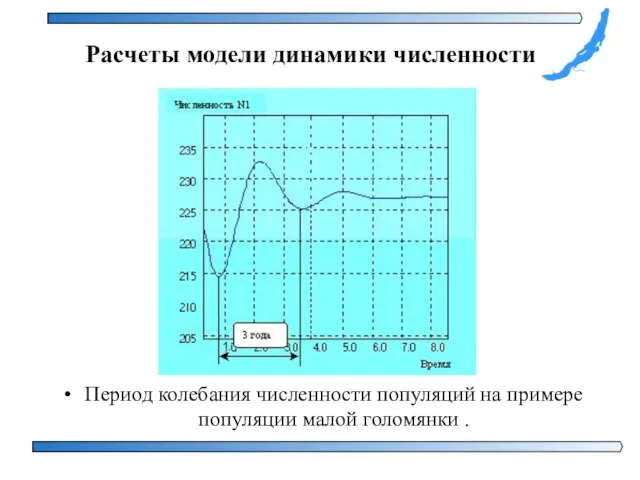
Период колебания численности популяций на примере популяции малой голомянки .
Расчеты модели динамики численности

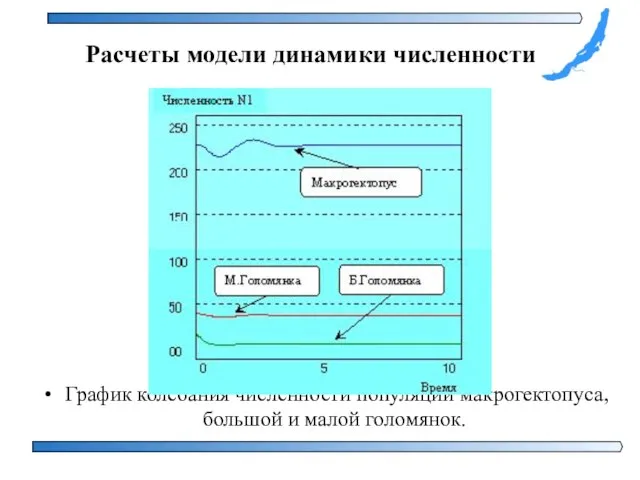
График колебания численности популяций макрогектопуса, большой и малой голомянок.
Расчеты модели динамики численности

1. Разработана модель динамики численности популяций макрогектопуса, малой голомянки и большой голомянки.
2. Модель построена на трех вспомогательных моделях: модели макрогектопуса, большой и малой голомянки. Каждая из вспомогательных моделей описывает стационарное состояние популяций.
3. Обратные связи устанавливаются через изменение коэффициента смертности для макрогектопуса и сеголеток голомянок и через коэффициенты репродуктивности для большой и малой голомянок.
4. Модель ведет себя устойчиво.
5. Поведение модели не противоречит поведению реальной системы:
- период колебаний полученной модели составляет 3 года;
- соотношения численностей популяций макрогектопуса, большой и малой голомянок соответствуют известным экспериментальным данным.
Результаты

Часть III
Построение межгодовой модели взаимодействия потоков биомасс в трофическом звене популяций макрогектопуса, большой и малой голомянок.

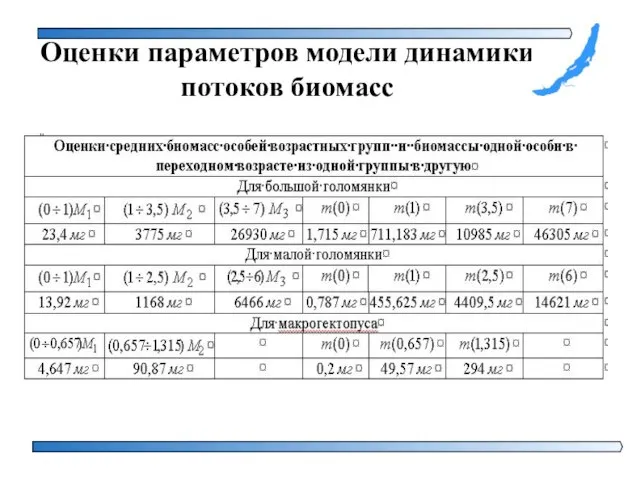
Оценки параметров модели динамики потоков биомасс
Располагая функциями зависимости биомассы особи от возраста:
- для особей голомянок зависимость задается таблично по данным Старикова В.Г.
-для особей макрогектопуса
Можно получить :

Оценки параметров модели динамики потоков биомасс

Общий вид балансового уравнения для биомасс возрастных групп макрогектопуса, большой и малой голомянок
(2)
здесь Вi - биомасса i-ой возрастной группы;
- входящий поток биомассы из i-1 возрастной группы;
Рi - продукция i-ой возрастной группы;
- поток выбывающей биомассы за счет выедания;
- поток выбывающей биомассы в связи с переходом в i+1 возрастную группу.
,
где
– средняя биомасса особей i-ой возрастной группы;
– биомасса одной особи в переходном возрасте из i-ой возрастной группы в (i+1)-ю;
– предельный возраст особи в i-ой возрастной группе.

Структура модели динамики потоков биомасс популяций макрогектопуса, большой и малой голомянок
Для малой голомянки: Для большой голомянки:
Для макрогектопуса:

Конкретизированный вид модели динамики потоков биомасс
Для малой голомянки: Для большой голомянки:
Для макрогектопуса:

Параметры модели
,где
, , - коэффициент репродуктивности (количество потомства в год от одной особи) для большой, малой голомянок и макрогектопуса соотв-но.
, где - параметр, определяющий максимальное время пребывания особи в данной возрастной группе.

Параметры модели
где - рацион рыб старших возрастов для стационарного случая
Вспомогательные переменные модели:

Значения параметров моделей в состоянии равновесия популяций
Малая голомянка –
Большая голомянка –
Макрогектопус –

Начальные условия модели динамики потоков биомасс популяций макрогектопуса, большой и малой голомянок
Для малой голомянки: Для большой голомянки:
Для макрогектопуса:
Как показали экспериментальные расчеты, модель находится в устойчивом равновесии.

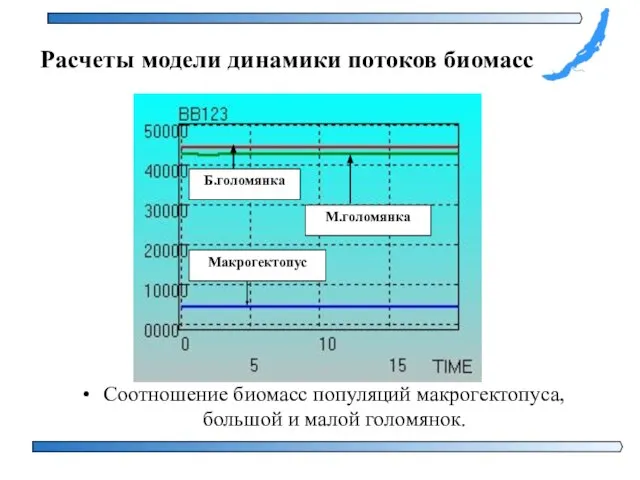
Соотношение биомасс популяций макрогектопуса, большой и малой голомянок.
Расчеты модели динамики потоков биомасс

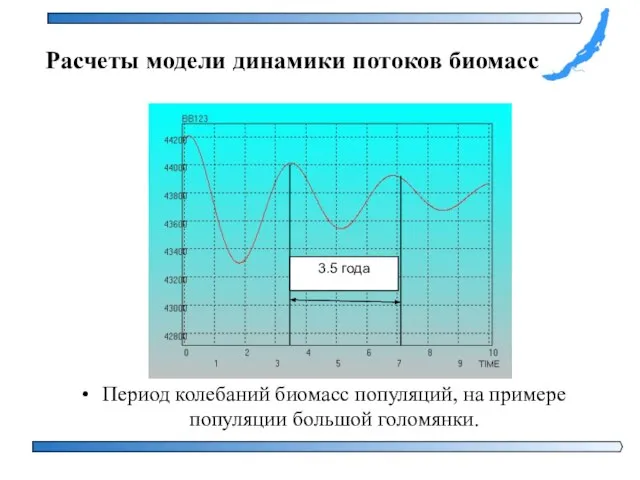
Период колебаний биомасс популяций, на примере популяции большой голомянки.
Расчеты модели динамики потоков биомасс

Полученные результаты
Построена модель, описывающая динамику потоков биомасс трофического звена «макрогектопус, большая и малая голомянки» экосистемы пелагиали озера Байкал.
Период колебаний полученной модели составляет около 3,5 лет, что не противоречит поведению реальной системы.
Соблюдаются соотношения биомасс популяций макрогектопуса, большой и малой голомянок.
Модель ведет себя устойчиво.

Итоги на текущий момент
Разработаны:
Методики оценки коэффициентов смертности.
Получены оценки:
- коэффициентов смертности для каждой возрастной группы популяций;
- коэффициентов рождаемости для каждой возрастной группы популяций;
- средней биомассы особи для каждой из возрастных групп популяций;
- потоков биомасс для каждой из популяций.
,
,
,
.

Итоги на текущий момент
Построены модели:
- модель, описывающая годовую динамику численности популяций в трофическом звене «макрогектопус, большая и малая голомянки» экосистемы пелагиали озера Байкал.
- модель, описывающая годовую динамику потоков биомасс в трофическом звене «макрогектопус, большая и малая голомянки» экосистемы пелагиали озера Байкал.
Результаты экспериментальных расчетов на моделях показали:
Период колебаний полученных моделей составляет около 3 - 3,5 лет, что не противоречит поведению реальной системы.
Модели ведут себя устойчиво, после возмущений сходятся к одному и тому же равновесному состоянию.
Соотношения численностей и биомасс популяций макрогектопуса, большой и малой голомянок близки к имеющимся экспериментальным данным.