Математика

Подготовка детей к вычислительной деятельности:
Ознакомление с цифрами.
Основные цели работы педагога при знакомстве детей с цифрами:
•научить детей узнавать образ цифры в различных изображениях
(печатная цифра, письменная цифра, стилизованная цифра типа цифры на почтовом индексе и т. п.);
•научить детей соотносить слово - числительное и цифру. Полезно учить детей запоминать контур цифры не только визуально (глазами), но и двигательно-осязательно (кинестезически).

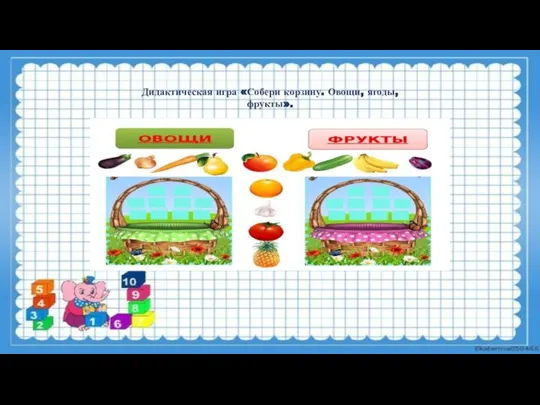
Дидактическая игра «Собери корзину. Овощи, ягоды, фрукты».

2. Усвоение состав числа из единиц и двух меньших чисел.
Ознакомление с составом числа из единиц.
В старшей и подготовительной группах детей знакомят с составом числа из единиц чисел первого десятка (5 -
это 1,1,1,1 и еще 1). Для того чтобы подчеркнуть состав множества (из
элементов) и на этой основе дать детям представление о составе числа (из единиц), подбирают такие совокупности, в которых каждый предмет отличается от других. Используются как предметы, объединенные одним родовым понятием (комплекты игрушек, посуда, мебель и т.д.), так и предметы одного вида, отличающиеся друг от друга либо окраской, либо размером, либо формой
(матрешки, флажки и т.д.)

Детей учат, рассматривая множества, рассказывать, как составлена группа, называть каждый элемент и их общее количество. Например:
«Число пять составлено так: 1 тарелка, 1 кружка, 1
кастрюля, 1 сковородка, 1 чайник — всего 5 предметов
посуды».
«Число три составлено так: 1 цилиндр, 1 куб, 1 шар —
всего 3 фигуры».

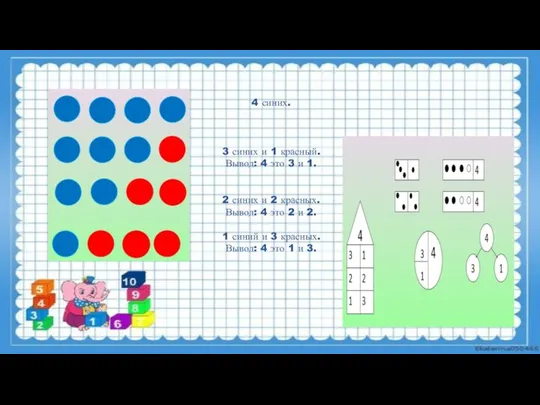
Ознакомление с составом числа из двух меньших чисел.
Воспитатель выкладывает на наборном полотне в ряд 4 кружка
одного цвета, просит детей сказать, сколько всего кружков (4
кружка синего цвета: 1, 1, 1 и еще 1). «Группу из 4 кружков можно
составить и по-другому», – говорит воспитатель и поворачивает
четвертый кружок обратной стороной. «Как теперь составлена
группа? – спрашивает педагог (3 кружка синего цвета и 1 кружок
красного цвета, а всего – 4 разноцветных кружка).
Воспитатель делает вывод, что число 4 можно составить из чисел 3
и 1, а 3 и 1 вместе составляют 4. Затем, поворачивает обратной
стороной второй кружок, и дети рассказывают, что теперь группа
составлена из 2 синих и 2 красных кружков. После этого
делается вывод о том, что число 4 можно составить так: 2 и 2 и т.
д.. Данное упражнение наглядно выявляет состав числа, отношение
целого и части, поэтому с него целесообразно начинать
знакомство детей с составом чисел.

4 синих.
3 синих и 1 красный.
Вывод: 4 это 3 и 1.
2 синих и 2 красных.
Вывод: 4 это 2 и 2.
1 синий и 3 красных.
Вывод: 4 это 1 и 3.

3. Деление целого на части.
Обучение строится на общих и функциональных зависимостях целого и части:
• часть всегда меньше целого, а целое больше части; равенство частей целого между собой;
• функциональная зависимость между количеством и размером частей: чем больше количество частей, на которое делится целое, тем меньше каждая часть, и, наоборот, чем больше часть, тем на меньшее количество частей разделено целое.
Деление целого на части осуществляется практически путем складывания с последующим разрезанием или путем разрезания.

Задачи обучения:
• научить детей делить предмет на две и четыре равные части путем разрезания или последовательного складывания плоских предметов пополам;
• сформировать представление о зависимости целого и части, уметь воспринимать неразделенный предмет не только как целое, но и как воссозданный из частей;
• упражнять в способе сравнения частей, полученных при делении целого на равные части, путем наложения, уточнить значение слова равенство;
• способствовать развитию самостоятельности мышления, сообразительности, упражнять детей в нахождении новых способов деления, выявления
зависимостей

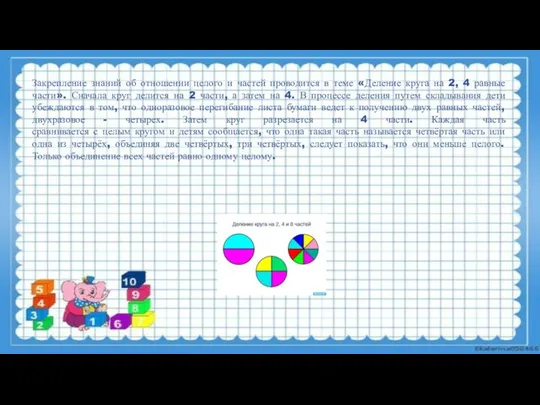
Закрепление знаний об отношении целого и частей проводится в теме «Деление круга на 2, 4 равные части». Сначала круг делится на 2 части, а затем на 4. В процессе деления путем складывания дети убеждаются в том, что одноразовое перегибание листа бумаги ведет к получению двух равных частей,
двухразовое - четырех. Затем круг разрезается на 4 части. Каждая часть
сравнивается с целым кругом и детям сообщается, что одна такая часть называется четвёртая часть или одна из четырёх, объединяя две четвёртых, три четвёртых, следует показать, что они меньше целого. Только объединение всех частей равно одному целому.

Воспитатель вводит новые выражения одна вторая (1/2), одна
четвертая (1/4), но с записью этих чисел детей не знакомят.
Соединяя части (как бы оставляя листы целыми), дети
раскладывают их один под другим, показывают 1 из 2 частей, 1 из
4 частей, сравнивают размер 1/2 и 1/4 части и их количество. Что
меньше: целый лист или половина? Что больше: половина или 1
из 4 частей, 1/4? Какая часть меньше всех? Почему? И т. п.

Обучение детей решению задач.
Этапы обучения решению задач:
1 этап: обучение составлению задач. Дети усваивают структуру задачи, выделяют условие и вопрос, осознают особое значение числовых данных. В содержании задач находится отражение окружающей жизни.

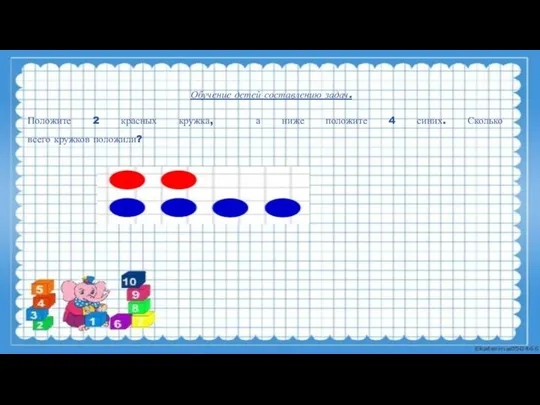
Положите 2 красных кружка, а ниже положите 4 синих. Сколько
всего кружков положили?
Обучение детей составлению задач.

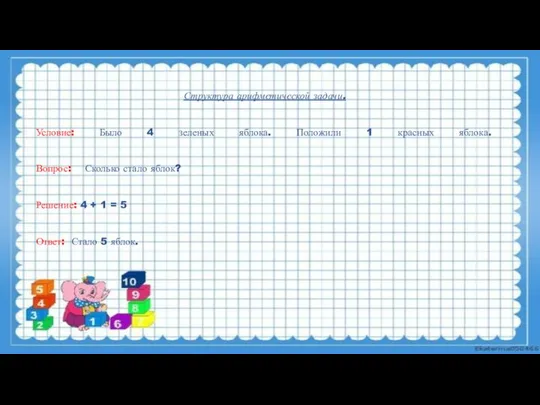
Структура арифметической задачи.
Условие: Было 4 зеленых яблока. Положили 1 красных яблока.
Вопрос: Сколько стало яблок?
Решение: 4 + 1 = 5
Ответ: Стало 5 яблок.

Обучению понимания, чем задача отличается
от рассказа, пословиц и загадок
В задаче обязательно должно присутствовать не менее 2 чисел
и обязательно содержаться вопрос. Необходимо учить детей рассуждать:
• Есть ли в задаче числа?
• Сколько чисел?
• Есть ли вопрос в задаче?
На стоянке стояли 3 машины. Приехала ещё одна. На стоянке много
машин.
- Я думаю это задача: есть два числа, её можно решить. Рассуждая с
детьми, приходим к выводу, что это не задача, её нельзя решить, т.к.
нет вопроса.

2 этап: обоснованно выбирать действия сложения или вычитания, правильно пользоваться приемами присчитывания и отсчитывания по одному, прибавляя или вычитая сначала число1, 2, а позже 3.
I этап: 1. Дается образец составления задачи воспитателем.
2. Разбор задачи по частям. Дается понятие «условие» и «вопрос».
3. Затем идет закрепление структуры задачи, причем каждый раз выделяя условие и вопрос.
II этап: 1. Учить записывать решение задачи при помощи цифр и знаков. 2.Учить понимать смысл задачи, почему именно нужно сложить
или вычесть.

III этап - формулировка арифметического действия:
• арифметическое действие должно быть сформулировано полно и правильно;
• упражнять детей в записи и чтении записи арифметического действия;
• слова «сложить, вычесть, получится, равняется» являются специальными
математическими терминами и дети должны их запомнить.
IV этап - учат приемам вычисления присчитывание и отсчитывание единицы.
Присчитывание - это прием, когда к известному уже числу прибавляется второе известное слагаемое, которое разбивается на единицы и присчитывается последовательно по 1
3 + 2 = 3 + 1 + 1 = 5
Отсчитывание - это прием, когда от известной уже суммы вычитается число (разбитое на единицы) последовательно по 1
5 – 2 = 5 – 1 – 1 = 3

Виды задач:
задачи – драматизации.
Отражают жизнь самих детей, т. е. то, что они только что делали или обычно делают. Дети учатся составлять задачи про самих себя,
рассказывать о действиях друг друга, ставить вопрос для
решения, поэтому структура задачи на примере задач-
драматизаций наиболее доступна детям. Важно, чтобы здесь наглядно представлять числовые данные, а не ответ на вопрос.
Сережа положил в коробку 4 карандаша, а Света 1 карандаш. Сколько всего карандашей в коробке?

Задачи – иллюстрации
(по картинкам, по игрушкам).
Служат дальнейшему развитию самостоятельности и накоплению опыта установления количественных отношений по картинкам и по игрушкам. С первой задачей по картинке знакомила детей сама. Учила рассмотреть рисунок, выделить числовые данные и те жизненные действия, которые привели к изменению количественных отношений.

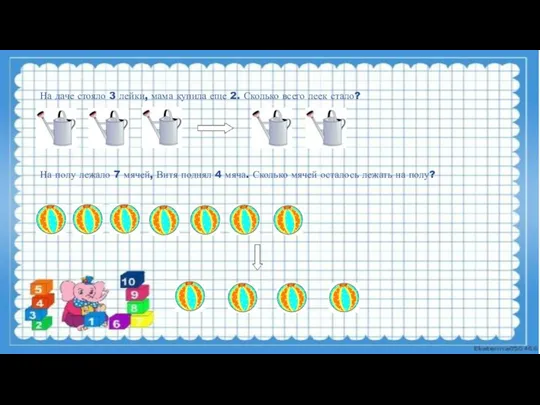
На даче стояло 3 лейки, мама купила еще 2. Сколько всего леек стало?
На полу лежало 7 мячей, Витя поднял 4 мяча. Сколько мячей осталось лежать на полу?

Устные задачи.
После того, как был освоен смысл действий, который надо было произвести, дети смогли решать и такие задачи, которые основаны на их опыте. Например, «На день рождения Саше подарили 3 машинки, да еще 1 паровоз. Сколько игрушек подарили Саше?»
Может быть использован такой прием: рассказывать детям задачу и предлагать им изобразить условие с помощью кружков, овалов или отложить косточки на счетах, или счетных палочках. Учить детей запоминать задачу с первого раза. Следить за тем, чтобы в задачах дети правильно отражали жизненные связи, зависимость. Каждый раз обсуждать, бывает ли так на самом деле.