Matrixnet

Линейная регрессия
Дано: K N-мерных самплов {xi} для каждого известно значение функции {fi}
Найти: вектор a, такой что aTxi= fi
Решение: a=(XTX)-1XTf

Регуляризация
Когда данных мало простое решение не работает
Нужна какая-то дополнительная информация, например, мы можем сказать, что мы хотим “маленький” или “простой” вектор a
Меры простоты:
L0 = feature selection
L1 = lasso
L2 = ridge = по Тихонову [a=(XTX+λI)-1XTf]

L1 регуляризация
Итеративный алгоритм L1 регуляризации
У нас есть текущий “остаток” ri, который в начале равен fi
На каждой итерации мы
Выбираем самый похожий на ri фактор и считаем с каким множителем α нам нужно его брать
Добавляем λα к коэффициенту при этом факторе (λ < 1)
Считаем новый остаток ri
http://www-stat.stanford.edu/~tibs/lasso.html

Нелинейные модели
Если бы у нас были пропорциональные релевантности независимые факторы, нам бы хватило линейной регрессии
Это не так и нам понадобятся нелинейные модели
Полиномиальные
“Нейронные сети”
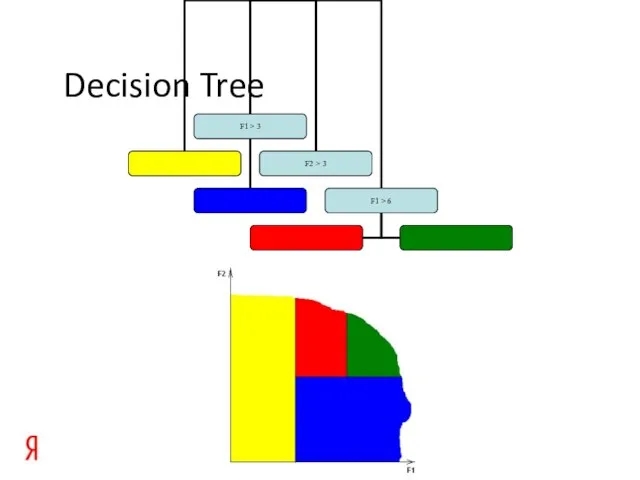
Decision Trees
…

Decision Tree

Boosting
Построение strong learner как комбинации “weak learners”
Связь с L1 регуляризацией
weak learner = единственный фактор с коэффициентом
strong learner = линейная регрессия c L1 регуляризацией
Для более сложного weak learner boosting дает сложно формализуемую sort of L1 регуляризацию

Bagging
На каждой итерации будем брать не все самплы, а их случайное подмножество
Магическим образом более устойчиво
Defeats boosting impossibility argument (http://velblod.videolectures.net/2008/pascal2/icml08_helsinki/long_rcn/icml08_long_rcn_01.ppt)

Limit on decision tree leafs
Дисперсия ошибки значения в листе пропорциональна 1/N, где N – количество самплов в листе
Введем ограничение – в кошерном дереве должно быть не меньше 10 самплов обучающей выборки на лист
Наш лимит ограничивает ошибку аппроксимации “выравнивая” ее по выборке

TreeNet
TreeNet товарища Friedman-a это Boosted Decision Tree с Bagging и ограничением на минимальное количество самплов в листе
http://www.salford-systems.com/doc/GreedyFuncApproxSS.pdf
http://www.salford-systems.com/doc/StochasticBoostingSS.pdf

MatrixNet
http://seodemotivators.ru/

MatrixNet
MatrixNet отличается в 3-х моментах
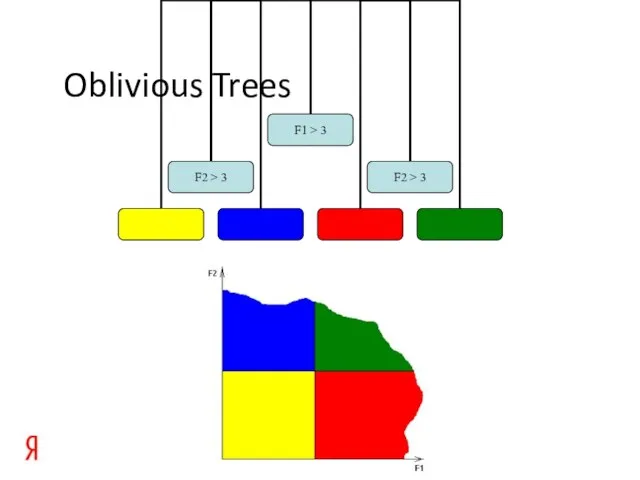
Использование Oblivious Trees
Регуляризация значений в листах вместо ограничения на количество самплов в листе
Зависимость сложности модели от итерации (начинаем с простых моделей, заканчиваем сложными)

Oblivious Trees

Регуляризация в листьях
Вместо ограничения на количество самплов в листьях будем “регуляризовать” значение в листе
Например, если домножить значение в листе на sqrt(N/(N+100)), где N – число самплов в листе, то результаты улучшатся.
Оптимальный способ регуляризации, видимо, зависит от выборки

Другие целевые функции
А что, если вместо квадратичной ошибки мы хотим оптимизировать что-нибудь другое? Например, для задач классификации больше подходит средний log(p), где p – вероятность, назначенная моделью правильному ответу
Получаем обычную задачу максимизации функции, которую можно решать
Градиентным спуском = gradient boosting = greedy function approximation
Методом Ньютона = logit boost для классификации

Gradient boosting
На каждом шаге boosting-a вместо невязки ri мы аппроксимируем производную целевой функции в текущей точке
Размер шага зависит от величины производной, т.е. от гладкости функции
Вместо шага по производной в текущей точке мы можем посчитать куда приведет нас производная и шагать в направлении финальной точки траектории

Ranking
А что же делать, если мы хотим научиться ранжировать?
Целевая функция для ranking (NDCG/pFound/whatever) задана на порядках и разрывна (описание pFound http://romip.ru/romip2009/15_yandex.pdf)
Нужна какая-то непрерывная замена. Замены делятся на классы
Pointwise (rmse, классификация, …)
Pairwise (RankNet, …)
Listwise (SoftRank, …)

Luce-Plackett model
Luce-Plackett model позволяет нам назначить вероятности всем перестановкам, если у нас есть веса документов {wi}
Вероятность перестановки вычисляется рекурсивно. Вероятность поставить документ k на первое место равна wk / (w1 + w2 + … + wn), далее аналогично считаем вероятность выбрать второй документ из оставшихся и т.д. Произведение этих вероятностей равно вероятности перестановки.

Expected pFound
Для каждой перестановки мы можем посчитать ее pFound(perm). Также мы знаем вероятность этой перестановки PLP(perm)
Просуммировав pFound(perm) * PLP(perm) по всем перестановкам получим expected pFound
Expected pFound непрерывен и мы можем максимизировать его с помощью gradient boosting
Вместо pFound мы можем подставить любую нужную нам меру